Работа внешних сил при вращательном движении твердого тела.
Найдем работу, которую совершают силы при вращении тела вокруг неподвижной оси Z.
Пусть на массу 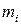 действуют внутренняя сила
действуют внутренняя сила 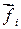 и внешняя сила
и внешняя сила 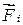 (результирующая сила
(результирующая сила 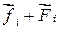 лежит в плоскости, перпендикулярной оси вращения) (рис. 4.19). Эти силы совершают за время dt работу:
лежит в плоскости, перпендикулярной оси вращения) (рис. 4.19). Эти силы совершают за время dt работу:
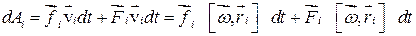 .
.
Осуществив в смешанных произведениях векторов циклическую перестановку сомножителей, находим:
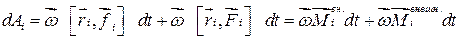 ,
,
где 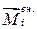 ,
, 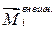 – соответственно, моменты внутренней и внешней сил относительно точки «О».
– соответственно, моменты внутренней и внешней сил относительно точки «О».
Просуммировав по всем элементарным массам, получим элементарную работу, совершаемую над телом за время dt:
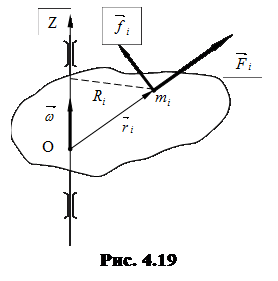
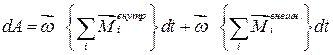 .
.
Сумма моментов внутренних сил равна нулю. Тогда, обозначив суммарный момент внешних сил через 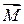 , придем к выражению:
, придем к выражению:
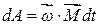 .
.
Известно, что скалярным произведением двух векторов называется скаляр, равный произведению модуля одного из перемножаемых векторов на проекцию второго на направление первого, учтя, что 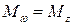 , (направления оси Z и
, (направления оси Z и 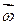 совпадают), получим
совпадают), получим
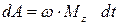 ,
,
но w·dt=dj, т.е. угол, на который поворачивается тело за время dt. Поэтому
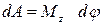 .
.
Знак работы зависит от знака Mz, т.е. от знака проекции вектора 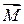 на направление вектора
на направление вектора 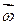 .
.
Итак, при вращении тела внутренние силы работы не совершают, а работа внешних сил определяется формулой 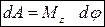 .
.
Работа за конечный промежуток времени находится путем интегрирования
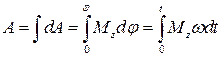 .
.
Если проекция результирующего момента внешних сил на направление 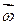 остается постоянной, то ее можно вынести за знак интеграла:
остается постоянной, то ее можно вынести за знак интеграла:
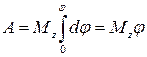 , т.е.
, т.е. 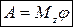 .
.
Т.е. работа внешней силы 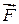 при вращательном движении тела равна произведению проекции момента внешней силы на направление
при вращательном движении тела равна произведению проекции момента внешней силы на направление 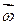 и угол поворота.
и угол поворота.
С другой стороны работа внешней силы, действующей на тело идет на приращение кинетической энергии тела (или равна изменению кинетической энергии вращающегося тела). Покажем это:
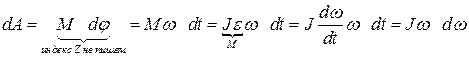
и тогда
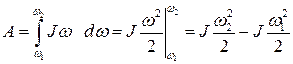 ;
;
Следовательно,
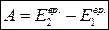 . (4.7)
. (4.7)
Самостоятельно:
Упругие силы;
Закон Гука.
| ЛЕКЦИЯ 7 |
Гидродинамика
Линии и трубки тока.
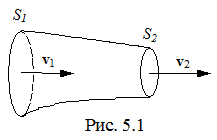 Гидродинамика изучает движение жидкостей, однако ее законы примени- мы и к движению газов. При стационарном течении жидкости скорость ее частиц в каждой точке пространства есть величина, независимая от времени и являющаяся функцией координат. При стационарном течении траектории частиц жидкости образуют линию тока. Совокупность линий тока образует трубку тока (рис. 5.1). Будем считать жидкость несжимаемой, тогда объем жидкости, протекающей через сечения S1 и S2 , будет одинаков. За секунду через эти сечения пройдет объем жидкости, равный
Гидродинамика изучает движение жидкостей, однако ее законы примени- мы и к движению газов. При стационарном течении жидкости скорость ее частиц в каждой точке пространства есть величина, независимая от времени и являющаяся функцией координат. При стационарном течении траектории частиц жидкости образуют линию тока. Совокупность линий тока образует трубку тока (рис. 5.1). Будем считать жидкость несжимаемой, тогда объем жидкости, протекающей через сечения S1 и S2 , будет одинаков. За секунду через эти сечения пройдет объем жидкости, равный
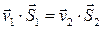 , (5.1)
, (5.1)
где 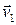 и
и 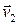 - скорости жидкости в сечениях S1 и S2, а вектора
- скорости жидкости в сечениях S1 и S2, а вектора 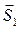 и
и 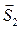 определяются как
определяются как 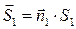 и
и 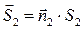 , где
, где 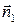 и
и 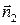 - нормали к сечениям S1 и S2. Уравнение (5.1) называют уравнением неразрывности струи. Из него следует, что скорость жидкости обратно пропорциональна сечению трубки тока.
- нормали к сечениям S1 и S2. Уравнение (5.1) называют уравнением неразрывности струи. Из него следует, что скорость жидкости обратно пропорциональна сечению трубки тока.
Уравнение Бернулли.
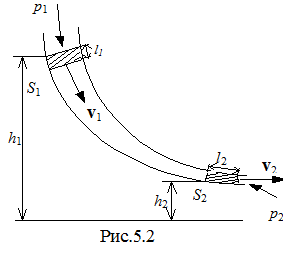 Будем рассматривать идеальную несжимаемую жидкость, в которой внутреннее трение (вязкость) отсутствует. Выделим в стационарно текущей жидкости тонкую трубку тока (рис. 5.2) с сечениями S1 и S2 , перпендикулярными к линиям тока. В сечении 1 за малое время t частицы сместятся на расстояние l1 , а в сечении 2 - на расстояние l2 . Через оба сечения за время t пройдут одинаковые малые объемы жидкости V = V1 = V2 и перенесут массу жидкости m=rV , где r - плотность жидкости. В целом изменение механической энергии всей жидкости в трубке тока между сечениями S1 и S2 , произошедшее за время t , можно заменить изменением энергии объема V , произошедшим при его перемещении от сечения 1 до сечения 2 . При таком движении изменится кинетическая и потенциальная энергия этого объема, и полное изменение его энергии
Будем рассматривать идеальную несжимаемую жидкость, в которой внутреннее трение (вязкость) отсутствует. Выделим в стационарно текущей жидкости тонкую трубку тока (рис. 5.2) с сечениями S1 и S2 , перпендикулярными к линиям тока. В сечении 1 за малое время t частицы сместятся на расстояние l1 , а в сечении 2 - на расстояние l2 . Через оба сечения за время t пройдут одинаковые малые объемы жидкости V = V1 = V2 и перенесут массу жидкости m=rV , где r - плотность жидкости. В целом изменение механической энергии всей жидкости в трубке тока между сечениями S1 и S2 , произошедшее за время t , можно заменить изменением энергии объема V , произошедшим при его перемещении от сечения 1 до сечения 2 . При таком движении изменится кинетическая и потенциальная энергия этого объема, и полное изменение его энергии
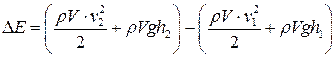 , (5.2)
, (5.2)
где v1 и v2 - скорости частичек жидкости в сечениях S1 и S2 соответственно; g - ускорение земного притяжения; h1 и h2 - высоты центра сечений.
В идеальной жидкости потери на трение отсутствуют, поэтому приращение энергии DE должно быть равно работе, совершаемой силами давления над выделенным объемом. При отсутствии сил трения эта работа:
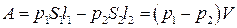 . (5.3)
. (5.3)
Приравнивая правые части равенств (5.2) и (5.3) и перенося члены с одинаковыми индексами в одну часть равенства, получим
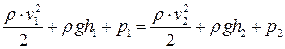 . (5.4)
. (5.4)
Сечения трубки S1 и S2 были взяты произвольно, поэтому можно утверждать, что в любом сечении трубки тока справедливо выражение
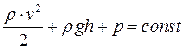 . (5.5)
. (5.5)
Уравнение (5.5) называется уравнением Бернулли. Для горизонтальной линии тока h = const , и равенство (5.4) приобретает вид
r 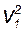 /2 + p1 = r·
/2 + p1 = r· 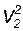 /2 + p2 , (5.6)
/2 + p2 , (5.6)
т.е. давление оказывается меньшим в тех точках, где скорость больше.
Силы внутреннего трения.
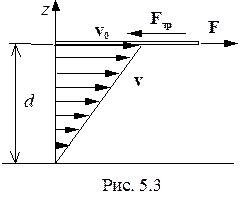 Реальной жидкости присуща вязкость, которая проявляется в том, что любое движение жидкости и газа самопроизвольно прекращается при отсутствии причин, вызвавших его. Рассмотрим опыт, в котором слой жидкости расположен над неподвижной поверхностью, а сверху его перемещается со скоростью
Реальной жидкости присуща вязкость, которая проявляется в том, что любое движение жидкости и газа самопроизвольно прекращается при отсутствии причин, вызвавших его. Рассмотрим опыт, в котором слой жидкости расположен над неподвижной поверхностью, а сверху его перемещается со скоростью 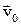 , плавающая на ней пластина с поверхностью S (рис. 5.3). Опыт показывает, что для перемещения пластины с постоянной скоростью необходимо действовать на нее с силой
, плавающая на ней пластина с поверхностью S (рис. 5.3). Опыт показывает, что для перемещения пластины с постоянной скоростью необходимо действовать на нее с силой 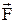 . Так как пластина не получает ускорения, значит, действие этой силы уравновешивается другой, равной ей по величине и противоположно направленной силой, которая является силой трения
. Так как пластина не получает ускорения, значит, действие этой силы уравновешивается другой, равной ей по величине и противоположно направленной силой, которая является силой трения 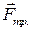 .Ньютон показал, что сила трения
.Ньютон показал, что сила трения
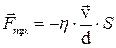 , (5.7)
, (5.7)
где d - толщина слоя жидкости, h - коэффициент вязкости или коэффициент трения жидкости, знак минус учитывает различное направление векторов Fтр и vo. Если исследовать скорость частиц жидкости в разных местах слоя, то оказывается, что она изменяется по линейному закону (рис. 5.3):
v(z) = = (v0/d)·z.
Дифференцируя это равенство, получим dv/dz = v0/d . С учетом этого
| |
Fтр=-h(dv/dz)S , (5.8)
где h - коэффициент динамической вязкости. Величина dv/dz называется градиентом скорости. Она показывает, как быстро изменяется скорость в направлении оси z. При dv/dz = const градиент скорости численно равен изменению скорости v при изменении z на единицу. Положим численно в формуле (5.8) dv/dz = -1 и S = 1, получим h = F . Отсюда следует физический смысл h: коэффициент вязкости численно равен силе, которая действует на слой жидкости единичной площади при градиенте скорости, равном единице. Единица вязкости в СИ называется паскаль-секундой (обозначается Па  с). В системе СГС единицей вязкости является 1 пуаз (П), причем 1 Па
с). В системе СГС единицей вязкости является 1 пуаз (П), причем 1 Па  с = 10П.
с = 10П.
