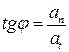Ускорение при криволинейном движении (тангенциальное и нормальное ускорение).
Если траектория движения материальной точки представляет собой кривую линию, то такое движение мы будем называть криволинейным.
При таком движении 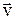 изменяется как по величине, так и по направлению. Следовательно, при криволинейном движении
изменяется как по величине, так и по направлению. Следовательно, при криволинейном движении 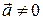 .
.
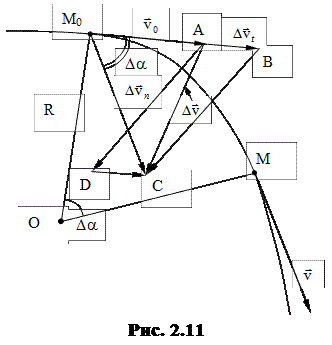 Рассмотрим движение материальной точки по криволинейной траектории (рис. 2.11). Вектор скорости движения в любой точке траектории направлен по касательной к ней. Пусть в точке M0 скорость
Рассмотрим движение материальной точки по криволинейной траектории (рис. 2.11). Вектор скорости движения в любой точке траектории направлен по касательной к ней. Пусть в точке M0 скорость 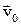 , а в точке М –
, а в точке М – 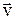 . При этом считаем, что промежуток времени Dt при переходе из точки М0 в точку М настолько мал, что изменением ускорения по величине и направлению можно пренебречь.
. При этом считаем, что промежуток времени Dt при переходе из точки М0 в точку М настолько мал, что изменением ускорения по величине и направлению можно пренебречь.
 Вектор изменения скорости
Вектор изменения скорости 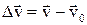 . (В данном случае разность 2х векторов
. (В данном случае разность 2х векторов 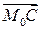 и
и 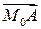 будет равна
будет равна 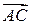 ). Разложим вектор
). Разложим вектор 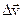 , который характеризует изменение скорости как по величине, так и по направлению на две составляющие
, который характеризует изменение скорости как по величине, так и по направлению на две составляющие 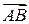 и
и 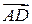 . Составляющая
. Составляющая 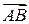 , которая является касательной к траектории в точке М0,характеризует изменение скорости по величине за время Dt, в течение которого была пройдена дуга М0М и называется тангенциальной составляющей вектора изменения скорости (
, которая является касательной к траектории в точке М0,характеризует изменение скорости по величине за время Dt, в течение которого была пройдена дуга М0М и называется тангенциальной составляющей вектора изменения скорости ( 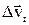 ). Вектор
). Вектор 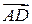 , направленный в пределе, когда Dt ® 0, по радиусу к центру, характеризует изменение скорости по направлению и называется нормальной составляющей вектора изменения скорости (
, направленный в пределе, когда Dt ® 0, по радиусу к центру, характеризует изменение скорости по направлению и называется нормальной составляющей вектора изменения скорости ( 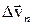 ).
).
Таким образом, вектор изменения скорости 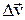 равен сумме двух векторов
равен сумме двух векторов 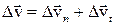 .
.
Тогда можно записать, что
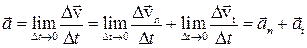 .
.
При бесконечном уменьшении Dt®0 угол Da при вершине DM0АС будет стремиться к нулю. Тогда вектором 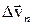 можно пренебречь по сравнению с вектором
можно пренебречь по сравнению с вектором 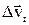 , а вектор
, а вектор
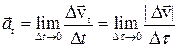
будет выражать тангенциальное ускорение и характеризовать быстроту изменения скорости движения по величине. Следовательно, тангенциальное ускорение численно равно производной от модуля скорости по времени 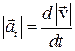 и направлено по касательной к траектории.
и направлено по касательной к траектории.
Вычислим теперь вектор 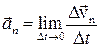 , называемый нормальным ускорением. При достаточно малом Dt участок криволинейной траектории можно считать частью окружности. В этом случае радиусы кривизны M0O и MO будут равны между собой и равны радиусу окружности R.
, называемый нормальным ускорением. При достаточно малом Dt участок криволинейной траектории можно считать частью окружности. В этом случае радиусы кривизны M0O и MO будут равны между собой и равны радиусу окружности R.
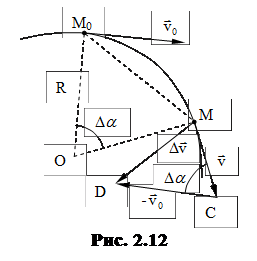
Повторим рисунок. ÐМ0ОМ = ÐМСD, как углы со взаимно перпендикулярными сторонами (рис. 2. 12). При малом Dt можно считать |v0|=|v|, поэтому DМ0ОМ = DМDC подобны как равнобедренные треугольники с одинаковыми углами при вершине.
Поэтому из рис. 2.11 следует
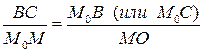 Þ
Þ 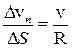 ,
,
но DS = vср.×Dt, тогда 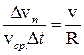 .
.
Переходя к пределу при Dt ® 0 и учитывая, что при этом vср. = v находим
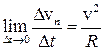 , т.е.
, т.е. 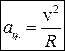 (2.5)
(2.5)
 Т.к. при Dt ® 0 угол Da ® 0, то направление этого ускорения совпадает с направлением радиуса R кривизны или с направлением нормали к скорости
Т.к. при Dt ® 0 угол Da ® 0, то направление этого ускорения совпадает с направлением радиуса R кривизны или с направлением нормали к скорости 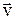 , т.е. вектор
, т.е. вектор 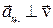 . Поэтому это ускорение часто называют центростремительным. Оно характеризует быстроту изменения скорости движения по направлению.
. Поэтому это ускорение часто называют центростремительным. Оно характеризует быстроту изменения скорости движения по направлению.
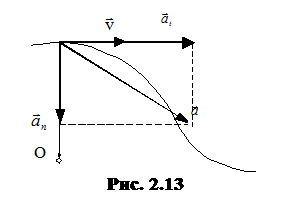
Полное ускорение определяется векторной суммой тангенциального и нормального ускорений 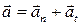 (рис. 2.13). Т.к. вектора этих ускорений взаимно перпендикулярны
(рис. 2.13). Т.к. вектора этих ускорений взаимно перпендикулярны 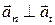 , то модуль полного ускорения равен
, то модуль полного ускорения равен 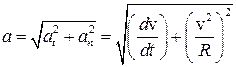 ; Направление полного ускорения определяется углом j между векторами
; Направление полного ускорения определяется углом j между векторами 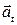 и
и 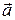 :
: