Уравнение моментов - дифференциальное уравнение вращательного движения твёрдого тела.

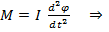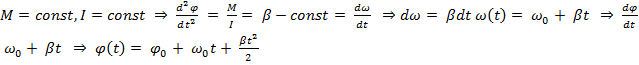Математически уравнение моментов и уравнение второго закона Ньютона относятся к одному типу и имеют одинаковое по виду решения. 1) –кинематическоеуравнение вращательного движения.

Динамика колебательного движения

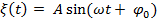- запись гармонического колебания, где A – амплитуда, 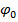- начальная фаза.

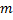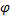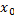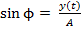- фаза (через функцию sinus) показывает, какую часть

смещение в данный момент времени составляет от амплитуды.

1) Пусть t = 0,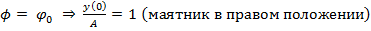

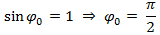
2) 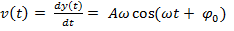- гармоническая функция

3)

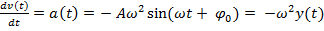
Так как 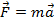, то 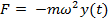= - -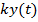уравнение динамики. Сила, пропорциональная смещению и направленная в сторону противоположную ему, вызывает колебательное движение.

.

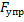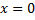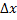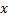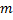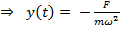Уравнение колебаний в канонической форме

Выведем на примере пружинного маятника.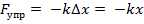

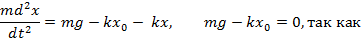
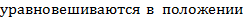равновесия.

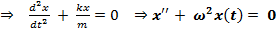– динамическое уравнение колебаний в каноническом виде.

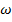- постоянная величина, характеризующая свойства системы. В нашем случае,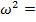

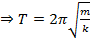
Где 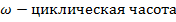. Решение уравнения вида: 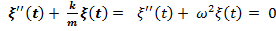есть гармоническая функция 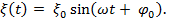Постоянные 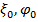–- функции начальных условий.

Tr 3BS1LhG+D+8vCxDWkS6oMZoRbmxhnT0+pJQUZtBf3O9dKXyItgkhVM61iZQ2r1iRnZiWtb+dTafI +bErZdHR4MNVI6dBMJeKau0/VNTytuL8sr8qhI+Bhk0UvvW7y3l7Ox5mnz+7kBGfn8bNCoTj0f3B cNf36pB5p5O56sKKBuE1nsceRYjiCIQHlrP74oQwXSwjkFkq/1fIfgEAAP//AwBQSwECLQAUAAYA CAAAACEAtoM4kv4AAADhAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnhtbFBL AQItABQABgAIAAAAIQA4/SH/1gAAAJQBAAALAAAAAAAAAAAAAAAAAC8BAABfcmVscy8ucmVsc1BL AQItABQABgAIAAAAIQApX8+NWwgAAJxBAAAOAAAAAAAAAAAAAAAAAC4CAABkcnMvZTJvRG9jLnht bFBLAQItABQABgAIAAAAIQBIanI14QAAAAoBAAAPAAAAAAAAAAAAAAAAALUKAABkcnMvZG93bnJl di54bWxQSwUGAAAAAAQABADzAAAAwwsAAAAA ">

Полное начальное условие: t = 0, .

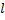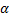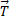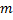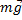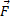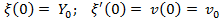Пример:пусть при t 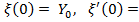= 0. 0.

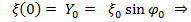
две неизвестные величины: 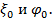Воспользуемся вторым условием:

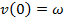
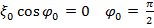. Тогда .

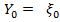Найдем каноническое уравнение математического маятника:

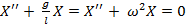- каноническое уравнение математического

маятника 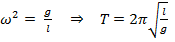. Уравнение: X(t)=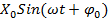

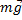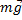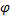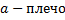Физический маятник -твёрдое тело, имеющее ось вращения.

Запишем уравнение моментов: , .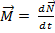

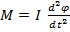Колебания – часть вращения.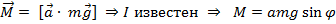

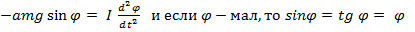
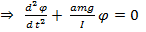–дифференциальное уравнение в каноническом виде.

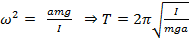. Уравнение колебаний: 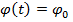Sin(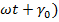

Динамика волнового движения. Волновое уравнение.Кинематическое уравнение волны: 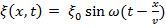–волнараспространяется в положительном направлении Ox. 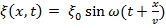– в отрицательном направлении оси OX.

Таким образом, 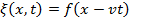Продифференцируем дважды и приравняем вторые производные:

=

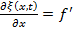
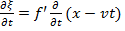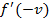
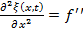
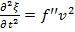
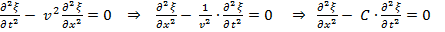– волновое уравнение в канонической форме,где C – характеризует упругие свойства среды и свойства колебательной системы.

Раздел 4. Законы сохранения

Закон сохранения импульса и его особенности. Закон сохранения момента импульса. Примеры: распад нейтрона, движение планет солнечной системы, гироскоп.

Работа сил. Потенциальная и кинетическая энергия. Работа и энергия вращения. Закон сохранения механической энергии. Примеры, практические задачи.

Закон сохранения импульса

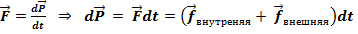
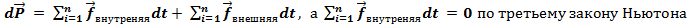
Следовательно, импульс меняется только под действием внешних сил. Отсюда:

1.

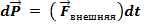
2.Если внешняя сила равна нулю, то система замкнута в механическом смысле.

Таким образом, для замкнутой системы импульс не изменяется.

Свойства закона сохранения импульса:

1.Этот закон носит векторный характер.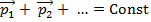

2.Этот закон справедлив для внутренних сил любой природы: консервативных или нет.

3.Для незамкнутых систем выполняется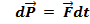

3.1.Закон сохранения и изменения импульса справедлив и в проекциях на оси координат: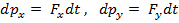

3.2.

Если в незамкнутой системе существует направление, на которое проекции внешних сил равны 0, то система считается замкнутой по этому направлению.

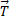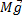Пример (баллистический маятник).

Система маятник –пуля не замкнута. 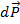= ( 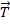+ + 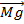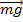) dt. В проекциях:

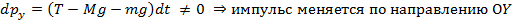
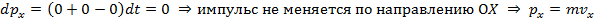
Таким образом, для получения точных данных надо пытаться добиться того, чтобы:

1.

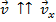
2. Необходимо брать нить большой длины, чтобы отклонение было меньше. Поскольку, как только маятник отклонится, система становится незамкнутой и по ОX. При большой нити горизонтальная составляющая силы натяжения нити при отклонении будет небольшой, поэтому импульс останется неизменным.
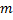
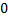
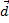
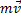
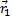