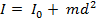Твёрдое тело. Уравнение моментов.

O

O’

Рассмотрим пример:Диск имеет неподвижную ось, относительно

которой он может свободно вращаться.

Приложенную к ободу диска силу разложим на две составляющие

.

Таким образом, проекция на OO' = 0, а проекция на OO' 0.

Следовательно: - вращения не будет, - вращение будет.

Необходимым и достаточным условием изменения (например, начала ) вращательного движения тела относительно неподвижной оси является наличие момента силы относительно этой оси. Наличие приложенной к телу силы необходимое, но не достаточное условие.

Вращательнодвижение вокруг неподвижной оси. Перейдём к полярной системе координыт

;

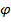Возьмем уравнение для одной точки твердого тела: (для i-ой точки).

Перейдем к моменту силы (умножим на : . Таким образом, для i-ой точки , где - момент импульса.

Определим, момент силы через момент импульса точки:

(перемножаются два коллинеарных векктора , Синус угола между ними равен нулю).

Следовательно, в скалярной форме для одной i-ой точки: . Моменты сил (как векторы) могут быть просуммированы по всем точкам тела:

Моментом инерции твердого тела относительно оси мы называем сумму произведений масс материальных точек тела на квадрат их расстояний до оси: .

Если нам удастся предварительно найти момент инерции тела- I относительно оси, то уравнение движения твёрдого тела будет описываться одним уравнением:

Тогда произвольное движение по теореме Эйлера будет описываться системой: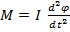

Уравнение моментов в общем случае нужно записать относительно некоторой мгновенной оси, выбор которой весьма не прост. Выясним физический смысл двух величин: массы и момента инерции.

Свойства массы:

1. Свойство тела сохранять состояние движения – инерция.

ускорение тем больше, чем меньше масса (тело меняет свое состояние движения тем меньше, чем больше масса). То есть масса определяет меру инерции.

2. m – мера кинетической энергии .

Аналогично, момент инерции является мерой инерции и кинетической энергии при вращении.

1. - то есть при одном и том жемоменте силы- M изменение состояния движения будет тем меньше, чем больше I. Следовательно, I – мера инерции во вращательном движении.

2. - чем больше момент инерции, при одной и той же скорости вращения, тем больше энергия. То есть I – мера кинетической энергии.

Примеры нахождения момента инерции:

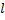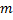1)Однородный стержень длины и массы m.

Пусть масса единицы длины = .

2)Обруча радиуса R и массы m.

: - масса единицы длины кольца.

3)Момент инерции диска, относительно оси, проходящей через центр масс .

4)Для цилиндра: 5) Для шара:

Теорема Штейнера-Гюйгенса

Момент инерции тела относительно произвольной оси равен моменту инерции тела, относительно оси проходящего через центр масс параллельно данной – 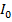, плюс произведение массы тела на квадрат расстояние между осями: