Математический аппарат физики. Векторы и операции с ними
Конспект лекций.
Часть I. Механика
Раздел 1. Введение
Математический аппарат физики. Векторы и операции с ними
Вектор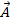 
характеризуется модулем (длиной) и направлением. Любой вектор равен своей длине, умноженной на единичный вектор 
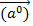своего направления: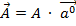 
 |
| |
 |
 |
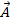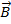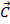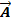и 
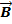, есть вектор 
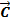,являющиеся диагональю паралелограмма, построенного на векторах 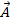и 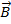как на сторонах. + = 
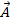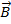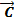.Длина вектора суммы:
| |
| |
 |
| |
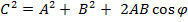
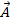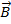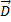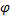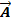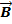и - есть вектор 
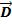,соединяющий концы вычитаемых векторов, приведенных к одному началу и направленный в сторону уменьшаемого. 
= 
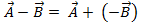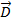
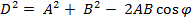
Изменение вектора (как по величине, так и по направлению): Если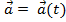 
, то
изменение за время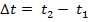 
, есть вектор 
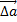(t)=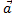 
(t2) - 
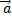(t1 ) Умножение векторов:
1.
 |
 |
 |
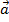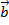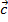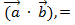
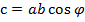
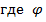- угол между векторами. 2. Векторное произведение есть вектор: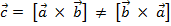 
Длина вектора :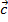 
.
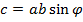Направление вектора :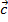 
, 
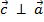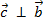, если смотреть с конца
| |
| |
| |
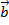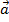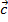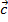, то направление кратчайшего поворота от первого вектора ко второму - против часовой стрелки. Разложение вектора на составляющие:
операция,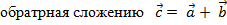 
.
Строим параллелограмм с диагональю 
и сторонами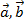 
 |
 |
 |
 |
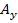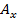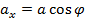, где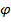 
- угол между осью и вктором. Если взять оси декартовой системы координат, то:
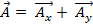- составляющие вектора.
– 
, 
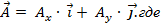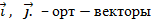
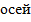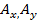-проекции вектора на оси.
Момент вектора относительно точки и оси:
1. Момент вектора относительно точки О – это вектор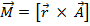 
Вектор 
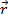-соединяет точку О с началом вектора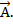 
2. Момент вектора относительно оси, проходящей через точку O – это проекция вектора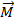 
на эту ось.
Дифференцирование функций.
1). 
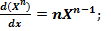2). 
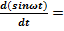
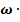cos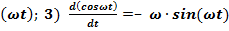 
.Здесь dx- бесконечно малое изменение величины x, dt- соответственно, величины t.
Дифференцирование вектора: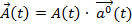 
, длина и направление - функции времени. Тогда
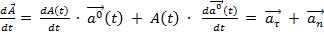
вектор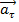 
– коллинеарен (параллелен) исходному 
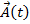, характеризует изменение
вектора только по величине.
Вектор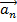 
– перпендикулярен исходному, характеризует изменение
вектора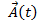 
только по направлению.
Пример. Пусть вектор 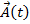меняется только по направлению, (вращается относительно своего начала), тогда производная от вектора будет равна: 
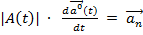. Найдём этот вектор.
Его направление совпадает с направлением вектора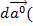 
t), соединяющего концы двух векторов 
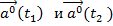Конец единичного вектора 
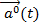описывает окружность единичного радиуса
и за бесконечно малое время dt опишет бесконечно малую часть этой окружности dS. При этом
длина дуги «почти» равна длине секущей (которая почти перпендикулярна к радиусу) т.е.
|d(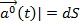 
=R 
= | 
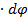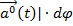= 1 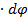. Модуль вектора | .| = | 
.
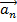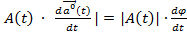Таким образом, вектор найден и по величине и по направлению.
Интегрирование.
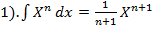+Const. 2). 
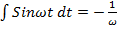cos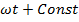 
; 
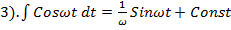
Если некоторая функция независимой переменной x есть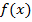 
, то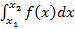 
численно равен площади под графиком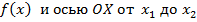 
Раздел 2. Кинематика
Материальная точка. Система отсчета. Траектория. Перемещение и путь. Скорость и ускорение. Тангенциальное и нормальное ускорения. Классификация движения по ускорению. Кинематика прямолинейного и вращательного движений точки. Кинематика колебательного и волнового движений. Примеры, практические задачи.
Задача 1.
Скорость материальной точки задана уравнениями: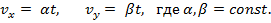 
Найти кинематическое уравнение движения и траекторию.
1) Запишем условие в векторной форме: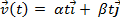 
2) Ускорение: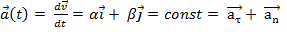 
3) 
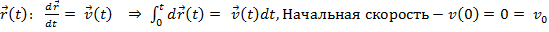по условию задачи.
4) Выберем начальное положение точки: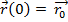 
.
Запишем кинематическое уравнение движения: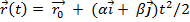 
В координатной форме:
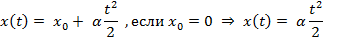
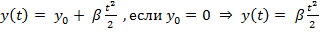
Для получения уравнения траектории необходимо исключить время :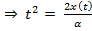 
Тогда уравнение траектории: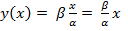 
- прямая линия.
Задача 2.
Материальная точка движется со скоростью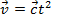 
Найти уравнение движения.
Начальные условия: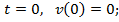 
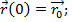
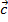-постоянный вектор
Решение.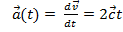 
; 
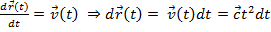Интегрируя , получим:
.
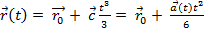Движение твердого тела
Твердое тело – это совокупность материальных точек, расстояние между которыми в процессе движения остается неизменным.
Степень свободы твердого тела– число независимых переменных, описывающих состояние данной системы.
Для того чтобы “найти” твердое тело в Декартовой системе координат необходимо знать координаты трех его точек, не лежащих на одной прямой. Так как каждая точка имеет три координаты, то 9 координат достаточно, чтобы определить положение твёрдого тела в пространстве. Однако число координат (степеней свободы) можно сократить, используя свойство неизменности расстояний между выбранными точками. Т.о – число степеней свободы твёрдого тела в трёхмерном пространстве может сведено к 6 (шести).
 |
 |
| |
 |
| |
; 
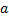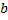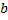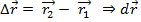
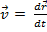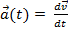- одинаковы для всех точек тела.
При поступательном движении достаточно знать закон движения одной точки твердого тела.
Вращательное движение.При вращении вокруг неподвижной оси радиус-векторы точек твердого тела, относительно точек отсчета, взятых на оси за любые равные промежутки времени совершают повороты на равные углы.
Если взять в качестве координат угол поворота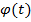 
, то любые точки будут иметь равные угловые скорости 
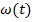и угловые ускорения 
.
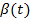Раздел 3. Законы динамики
Основная задача динамики. Первый закон Ньютона. Инерциальные системы отсчета. Взаимодействие тел. Сила. Масса и импульс тела. Второй закон Ньютона, и его особенности. Третий закон Ньютона и границы его применимости.
Твердое тело. Момент импульса, момент силы, момент инерции. Уравнение моментов – дифференциальное уравнение движения твердого тела. Уравнения динамики колебательного и волнового движений (волновое уравнение). Примеры, практические задачи.
Динамикаизучает движение материальной точки (тел) вместе с причинами, вызывающими это движение. Основная задача: по заданной силе найти закон движения тела.
Первый закон динамики:всякое тело движется прямолинейно и равномерно или находится в покое до тех пор и поскольку действие со стороны других тел не заставит его изменить это состояние движения. Важные следствия Первого закона:
1. Действие со стороны других тел (сила) необходима, чтобы изменить состояние движения.
2. Покой и равномерное прямолинейное движение есть два одинаковых состояния.
3. Механическое движение всегда относительно.
4. Первый закон позволяет выбрать инерциальную систему отсчета, то есть такую систему отсчета, в которой свободное тело движется прямолинейно и равномерно или покоится.
Первый закон позволяет ввести важные понятия:
Сила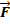 
–количественная мера действия одного тела на другое.
Масса. Свойство тела сохранять состояние движения – инерция. Количественная мера инерции - масса. Чем больше масса, тем меньше тело изменяет состояние движения.
Импульс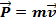 
. По первому закону действие одного тела на другое проявляет себя в изменении скорости или импульса: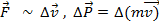 
.
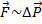Второй закон динамики:В качестве количественной меры действия (силы), Ньютон предложил взять скорость изменения импульса тела, на которое производится это действие:
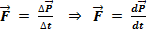(1)
Решения данного дифференциального уравнения при различных начальных условиях дают кинематические уравнения движения материальной точки в самых общих случаях.
Для тела переменной массы: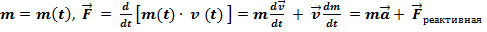 
Второй закон Ньютона в форме (1) наиболее общий, чем в форме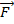 
= m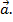 
Уравнение в форме: 
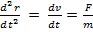(2) есть дифференциальное уравнение движения в переменных Ньютона (r,t). По заданной силе и начальным условиям решение (2) даёт кинематический закон движения 
.
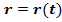Второй закон в другом виде:
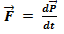Умножим скалярно на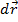 
)= 
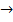
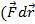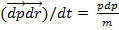т.к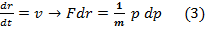 
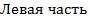(3) есть элементарная механическая работа. Энергия - есть способность системы (тела)совершить работу, тогда правая часть (3) есть элементарная энергия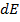 
При совершении работы силой (телом) энергия изменяется, то есть: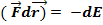 
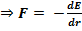. (4)
Таким образом, действие силы во времени изменяет импульс тела; действие силы в пространстве - изменяет энергию тела. Для получения кинематических уравнений движения нужно решать дифференциальное уравнение вида (1), (2).или (3),(4). В первом случае решение называется в переменных Ньютона, во втором, в переменных Гамильтона.
Уравнение (1) можно решить как в координатной, так и векторной формах.
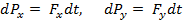
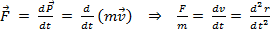=a 
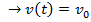+at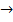
; 
: 
.
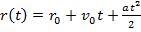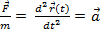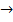
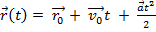Механическая энергия делится на энергию движения (кинетическую), зависящую от скорости движения (или импульса) тела и энергию, зависящую от положения (координат) взаимодействующих тел (потенциальную). Полная энергия: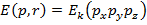 
+ 
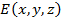Решение уравнения (3) в переменных Гамильтона обычно используется в системах, состоящих из большого числа элементов (частиц), в которых состояние системы определяется её энергетическим состоянием, а не координатами частиц: 
.
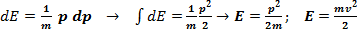Подробнее - во второй части физики – молекулярной и статистической физике.
Силы делятся по физической природе на:
1. Гравитационные 3. Сильные внутри атома и ядра
2. Электромагнитные 4.Слабые между элементарными частицами.
Третий закон динамики:
Каждому действию есть равное и противоположное противодействие. Или тела взаимодействуют с силами, равными по величине и противоположными по направлению.
| Земля |
| планета |
| 1 световой год |
 |
 |
Границы применения:Зависят от скорости передачи информации
Тела меняют положение, следовательно, какое-то время
закон не будет действовать. Закон будет выполняться
между гравитационным полем Земли и планетой. Но
между Землёй и планетой, как точечными телами,
действие закона будет запаздывать на время прихода
информации о перемещении.
Теорема Штейнера-Гюйгенса
Момент инерции тела относительно произвольной оси равен моменту инерции тела, относительно оси проходящего через центр масс параллельно данной –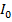 
, плюс произведение массы тела на квадрат расстояние между осями: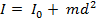 
Раздел 4. Законы сохранения
Закон сохранения импульса и его особенности. Закон сохранения момента импульса. Примеры: распад нейтрона, движение планет солнечной системы, гироскоп.
Работа сил. Потенциальная и кинетическая энергия. Работа и энергия вращения. Закон сохранения механической энергии. Примеры, практические задачи.
Закон сохранения импульса
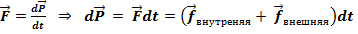
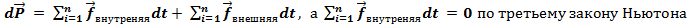
Следовательно, импульс меняется только под действием внешних сил. Отсюда:
1. 
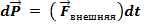
2.Если внешняя сила равна нулю, то система замкнута в механическом смысле.
Таким образом, для замкнутой системы импульс не изменяется.
Свойства закона сохранения импульса:
1.Этот закон носит векторный характер.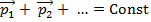 
2.Этот закон справедлив для внутренних сил любой природы: консервативных или нет.
3.Для незамкнутых систем выполняется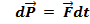 
3.1.Закон сохранения и изменения импульса справедлив и в проекциях на оси координат: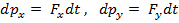 
3.2.
 |
| |
 |
 |
 |
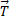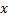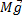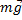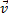Пример (баллистический маятник).
Система маятник –пуля не замкнута.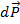 
= ( 
+ 
+ 
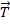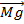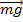) dt. В проекциях:
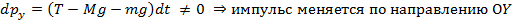
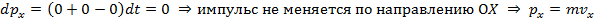
Таким образом, для получения точных данных надо пытаться добиться того, чтобы:
1. 
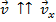
2. Необходимо брать нить большой длины, чтобы отклонение было меньше. Поскольку, как только маятник отклонится, система становится незамкнутой и по ОX. При большой нити горизонтальная составляющая силы натяжения нити при отклонении будет небольшой, поэтому импульс останется неизменным.
 |
 |
 |
 |
 |
 |
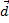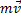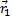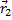Полевая теория
Любое тело создает вокруг себя поле – гравитационное поле.
Свойства гравитационного поля:
1) Оно непрерывно распределено в пространстве, проникает в другие поля и вещества.
2) Это поле действует с некоторой силой на все тела, помещенные в это поле.
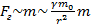
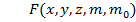– сила тяготения зависит не только от выбора точки поля (x,y,z) и массы тела, создающего поле ( 
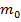,) , но и от массы «пробного» тела (m), что крайне не удобно для характеристики поля. Поэтому введем другую величину.
Напряженность гравитационного поля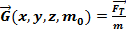 
- -численно равна силе, дейсвующей на единичную массу, помещённую в данную точку поля. Тогда закон примет вид:
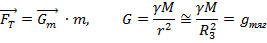
1) Поле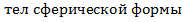 
имеет точно такую же структуру, что и точечное тело такой же массs M, помещенной в центре сферы. (для 
)
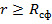2) Это поле цетральное (поле центробежных сил.)
То есть поле потенциально, то:
1) работа сил поля A зависит только от начальной и конечной точки, а не от траектории.
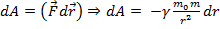Знак минус т.к. угол между силой и радиус-вектором 
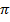Тогда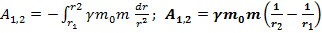 
2) Так как работа равна изменению энергии,то имеет смысл разность потенциальных энергий
тела в двух точках поля:
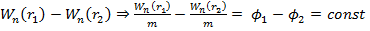Найдём эту энергию через работу
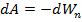
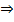
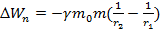. Тогда 
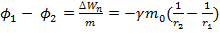-разность потенциалов двух точек гравитационного поля: численно равна работе сил поля по перемещению единичной массы из первой точки во вторую.
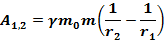
1. Если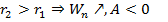 
Тело удаляется, работа совершается против сил поля (притяжения). Работа отрицательна, потенциальная энергия растет.
2. Если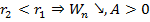 
. Тела сближаются силами поля, работа положительна, потенциальная энергия уменьшается.
3. Если принят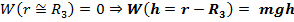ь: 
Здесь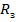 
-радиус Земли.
Так как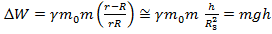 
.
4. 
= 
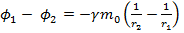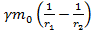
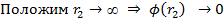Тогда потенциал произвольной точки поля :
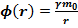–относительно бесконечности: численно равен работе, которую нужно совершить, чтобы единичную массу перенести из данной точки в бесконечность.
Определим энергии гравитационного поля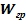 
.
Пусть имеем шар массы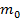 
и радиусом-R. Энергию гравитационного поля шара можно определить как работу по переносу всей массы тела в бесконечность. Так как потенциал поверхности будет меняться с изменением размеров шара (и его массы), то следует переносить массу б.малыми порциями dm. Тогда 
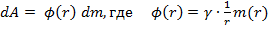-текущее значение потенциала поверхности шара. Выразим m(r):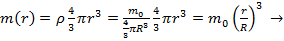 
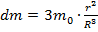dr и можно записать в явном виде: 
.
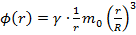Подставляя в выражение для работы: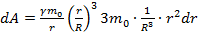 
=> 
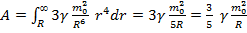Таким образом 
, 
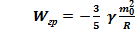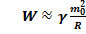
Примеры
1. Считая, что полная энергия электрона равна его гравитационной, получим: 
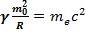
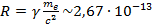см – совпадает с другими методами вычислений. 2..Применим последнюю формулу к произвольному гравитационному объекту:
= 
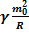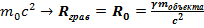Это гравитационный радиус объекта.
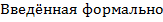величина 
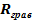оказалась чрезвычайно информативной и важной.
1) Можно оценить гравитационную энергию объекта.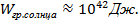 
(Посчитав плотность энергии, излучаемой Солнцем , учёные пришли к выводу о наличии еще каких- то источников энергии , в частности, энергию термоядерной реакции.
2) Если сравнить истинный радиус планеты и её гравитационный радиус, то при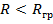 
, с планеты нельзя излучать никакие виды энергии ( в том числе и свет). То есть, мы эту планету не увидим. Следовательно, возникает ЧЁРНАЯ ДЫРА.
| |
 |
 |
 |
| |
 |
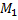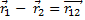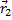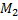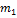и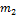 
. Одно движется в гравитационном поле другого от точки отсчета проведены радиус-векторы.
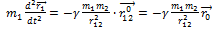, где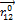 
- единичный вектор.
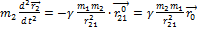
Начальные условия: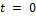 
, 
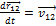, еще наложить условия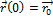 
Вычтем: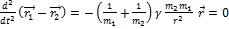 
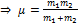– приведённая масса, тогда
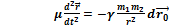- уравнение движения одного тела, относительно другого.
Решение этого уравнения достаточно сложное. Для качественных оценок можно использовать
законы сохранения:
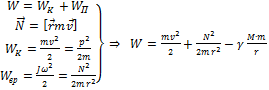Здесь два последних слагаемых есть функции координат (r) т.е потенциальная энергия- 
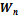,(Так как N = const по закону сохранения момента импульса
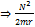функция от r)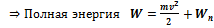 
Замечания Качественный анализ.
1) 
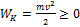кинетическая энергия тела может быть только положительной
: 
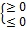но полное не может быть меньше 
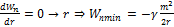
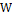
1. 
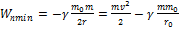- для частицы с массой m.
Единственное решение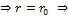 
движение строго по окружности с 
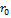. r
2. 
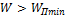, то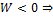 
существует два решения в некотором интервале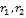 
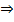движение по эллипсу.
3. 
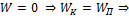движение по параболе (разомкнута относительно ).
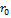4. 
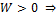движение по гиперболе (разомкнута вообще).
Теорема Кориолиса.
Абсолютное ускорение тела есть векторная сумма ускорений: относительного, переносного и кориолисова .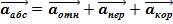 
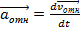
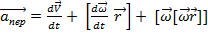Здесь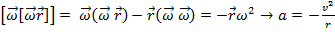 
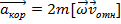
То есть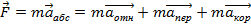 
.
S’: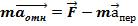 
- m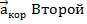 
закон динамики тела в S'.
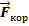= – 2m[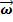 
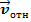],сила перпендикулярна к веторам скоростей.
Примеры:
1. Поступательная сила инерции. Пусть в системе S' находится математический маятник.
За ним наблюдают два наблюдателя: S- всегда неподвижен и S’- может двигаться. Механизм в покое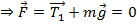 
.Сила натяжения и вес уравновешиваются. Оба наблюдателя по первому закону подтверждают это.
Теперь двинем систему с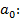 
Наблюдатель S: нить должна отклониться, чтобы результирующая сила F сообщила телу ускорение 
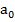.Для наблюдателя S’ маятник в покое, но отклонился так, что вес и натяжение не уравновешивают друг друга, он вынужден приписать ещё одну силу –ma0 чтобы удовлетворить первому закону механики.
, 
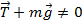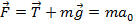- с точки зрения S, а с точки зрения S’ существует сила инерции: 
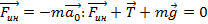– тогда маятник в покое.
2. Центробежная сила инерции Маятник вращается вокруг неподвижной оси. Для S- наблюдателя- при отклонении результирующая сила меняет направление вектора скорости. Для наблюдателя S’-вновь нужно ввести силу от оси вращения, чтобы сумма сил равнялась нулю и тогда выполниться первый закон.
Проявление сил инерции в движениях на Земле:
1) Меняется ускорение силы тяжести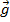 
. 
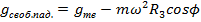
2) Форма земли – геоид. Составляющая ц.б. силы инерции сдвигает массу Земли к экватору.
3) Волга движется вверх также вследствие действия сил инерции.
4) 
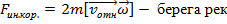, пассаты и муссоны.
Раздел 7. Элементы теории относительности. Примеры.
 |
 |
 |
| |
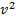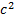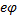1. Скорость света в вакууме не зависит от
скорости движения источника или приемника
т.е. скорость света С=const.
Эксперимент с электронами показал, что
максимальная скорость их движения не превышает «с», хотя энергия их растёт пропорционально работе источника: Объяснение кроется в зависимости массы от скорости.
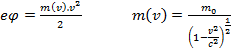
2. Все законы физики выполняются во всех инерциальных системах, то есть все наблюдатели S равноправны.
| |
| |
 |
| |
 |
 |
 |
| ’ |
| ’ |
| |
| ’ |
 |
 |
  |
  |
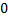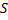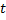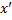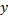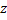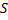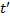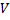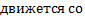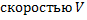В t = 0 S и S’ находятся в одной точке, потом происходит движение.
Разместим лампочку в 0. Фронт волны в S: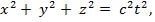 
Фронт сфера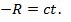 
В S’ такой фронт волны – сфера: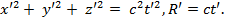 
При переходе из S в S’: равноправие наблюдателей удовлетворяется, если и координаты и время подвергнуть преобразованиям: y’=y; z’=z;
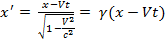(1), где 
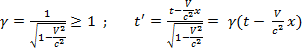(2)
При переходе из S’ в S: y=y’; z=z’;
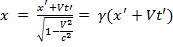(3) 
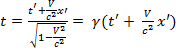(4).