Какое утверждение справедливо относительно приведенной теплоты, полученной системой в циклическом необратимом процессе? Неравенство Клаузиуса.

Количество теплоты, полученное системой при любом круговом процессе, делённое на абсолютную температуру, при которой оно было получено, неположительно.

Как определяется энтропия в термодинамике?

Функция состояния термодинамической системы.

365. Как выражается изменение энтропии идеального газа через 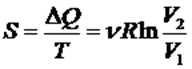начальные и конечные значения температуры и объема?

Как изменяется энтропия идеального газа при адиабатном расширении в вакуум?

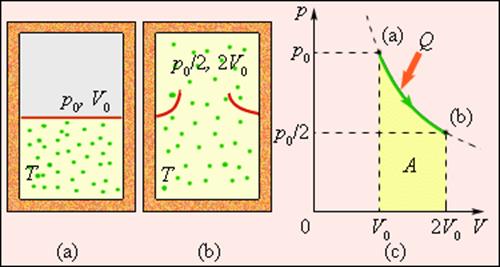
Расширение газа в пустоту. На рис. 1 (а) изображена жесткая адиабатическая оболочка, разделённая на две части перегородкой. В первоначальном состоянии газ заполняет одну часть, а в другой – вакуум. После устранения перегородки (рис.1 б) газ расширяется, заполняет всю оболочку, и устанавливается новое равновесное состояние. В этом процессе Q = 0, т.к. нет теплообмена с окружающими телами, и A = 0, т.к. оболочка недеформируема. Из первого закона термодинамики следует: ∆U = 0, т. е. внутренняя энергия газа осталась неизменной. Так как внутренняя энергия идеального газа зависит только от температуры, температура газа в начальном и конечном состояниях одинакова – точки на плоскости (p, V), изображающие эти состояния, лежат на одной изотерме. Все промежуточные состояния газа неравновесны и их нельзя изобразить на диаграмме.

Рисунок 1 иллюстрирует необратимый процесс расширения газа «в пустоту» в отсутствие теплообмена. Только начальное и конечное состояния газа в этом процессе являются равновесными, и их можно изобразить на диаграмме (p, V). Точки (a) и (b), соответствующие этим состояниям, лежат на одной изотерме. Для вычисления изменения ΔS энтропии можно рассмотреть обратимый изотермический переход из (a) в (b). Поскольку при изотермическом расширении газ получает некоторое количество теплоты от окружающих тел Q > 0, можно сделать вывод, что при необратимом расширении газа энтропия возросла: ΔS > 0.

Расширение газа в «пустоту». Изменение энтропии 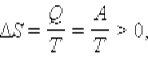где A = Q – работа газа при обратимом изотермическом расширении.

Как изменяется энтропия в обратимом адиабатном процессе?

Обратимый цикл Карно

Из п. 5.2 мы знаем, что в тепловой машине, работающей по принципу Карно, имеются три тела: холодильник, нагреватель, рабочее тело (газ).

Изменение энтропии газа в тепловой машине 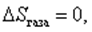так как газ возвращается в исходное состояние.

Изменение энтропии нагревателя:

.

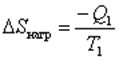(6.4.1)

Для холодильника:

.

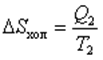(6.4.2)

.

.

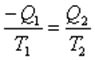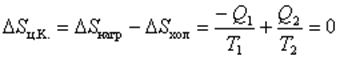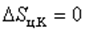или

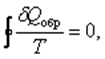
(6.4.3)

т.е. S – константа. Таким образом, мы пришли к выражению, полученному в п. 6.1, называемому равенство Клаузиуса.

368. Как изменяется энтропия в необратимом адиабатном процессе?

Необратимый цикл Карно

Мы знаем, что 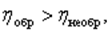т.е.

.

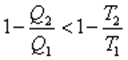(6.4.4)

Отсюд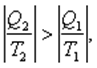а тогда .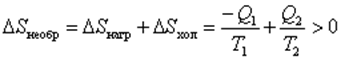

Таким образом,

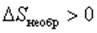или

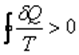
(6.4.5)

Это выражение называют неравенством Клаузиуса: при любом необратимом процессе в замкнутой системе энтропия возрастает (dS > 0).