Энергетическая яркость (лучистость)

В_е — Dвеличина, равная отношению энерге­тической силы света I_e S проек­ции этого элемента на плоскость, пер­пендикулярную направлению наблюде­ния:Dэлемента излуча­ющей поверхности к площади

В_еID=_еS.D/

Единица энергетической яркости — ватт на стерадиан-метр в квадрате (Вт/(ср•м²)).

Энергетическая освещенность (облу­ченность) Ее характеризует величину по­тока излучения, падающего на единицу освещаемой поверхности. Единица энерге­тической освещенности совпадает с едини­цей энергетической светимости (Вт/м²).

2. Световые величины. При оптических

измерениях используются различные при­емники излучения (например, глаз, фото­элементы, фотоумножители), которые не обладают одинаковой чувствительностью к энергии различных длин волн, являясь, таким образом, селективными (избира­тельными). Каждый приемник излучения характеризуется своей кривой чувстви­тельности к свету различных длин волн. Поэтому световые измерения, являясь субъективными, отличаются от объектив­ных, энергетических и для них вводятся световые единицы, используемые только для видимого света. Основной световой единицей в СИ является единица силы света — кандела (кд), определение кото­рой дано выше (см. Введение). Определе­ние световых единиц аналогично энергети­ческим.

Световой поток Ф определяется как мощность оптического излучения по вы­зываемому им световому ощущению (по его действию на селективный приемник света с заданной спектральной чувстви­тельностью) .

Единица светового потока — люмен (лм): 1 лм — световой поток, испускаемый точечным источником силой света в 1 кд внутри телесного угла в 1 ср (при равно­мерности поля излучения внутри телесного угла) (1 лм= 1 кд•ср).

Светимость R определяется соотно­шением

R=Ф/S.

Единица светимости — люмен на метр в квадрате (лм/м²).

Яркость В_j есть величина, равная отношению силы светаjсветящейся поверхности в некотором направлении I в этом направлении к площади S проекции све­тящейся поверхности на плоскость, перпендикулярную данному направле­нию:

В_j).j=I/(Scos

Единица яркости — кандела на метр в квадрате (кд/м²).

Освещенность E — величина, равная отношению светового потока Ф, падающе­го на поверхность, к площади S этой поверхности.0,2

21. Линии равной толщины и их локализация.

1. Линии равного наклона и их локализация.

Полосы равного наклона получаются при освещении пластинки постоянной толщины рассеянным светом а=const. Волны, падающие под углом, интерферируют и образуют соответствующую полосу – максимум интерференции.

Полосы равной толщины получаются при освещении пластинки непостоянной толщины параллельным пучкам света а=const.

13. Распространение электромагнитной волны в проводящих средах, комплексный показатель преломления, глубина проникновения.

В конце XIX века английский физик Дж.К.Максвелл на основе своих уравнений создал единую электромагнитную тео­рию световых волн, согласно которой, свет – это множество электромагнитных волн. Электромагнитная волна – это распростра­няющееся в пространстве электромагнитное поле, которое ха­рактеризуется векторами напряженностей Еи Н электрического и магнитного полей. Согласно теории Максвелла, вектора Еи Нперпендику­лярны друг другу и направ­лению распро­странения волны, откуда следует, что электромагнит­ные волны по­перечны (рис. 1.3).

Если среда, в кото­рой распространяется волна, однородная и изо­тропная, то векторыЕи Нудовлетворяют волновому уравне­нию:

где - оператор Лапласа, - фазовая ско­рость волны.

Если электромагнитная волна распространяется в на­правлении х, то волновые уравнения упрощаются:

Решения данных дифференциальных уравнений второго порядка можно представить в виде:

Е = Е₀sin (ωt-kx+φ); H = H₀sin (ωt-kx+φ).

Это уравнения плоской монохроматической электромаг­нитной волны, где Е₀ и Н₀ – амплитудные значения Е и Н, k = =ω/υ – волновое число, φ – начальная фаза колебания, х – рас­стояние, отсчитываемое вдоль направления распространения электромагнитной волны. Электромагнитная волна называется монохроматической, если в ней происходят колебания только одной частоты. Мгновенные значения Е и Н в любой точке про­странства связаны соотношением

,

где ε₀ и μ₀ – электрическая и магнитная постоянные, ε и μ – ди­электрическая и магнитная проницаемости среды. Колебания векторов Еи Н происходят синфазно, т.е. они одновременно об­ращаются в ноль и одновременно достигают максимальных зна­чений. Скорость распространения света в среде или фазовая скорость волны рассчитывается по формуле , где с – скорость света в вакууме.

Электромагнитное поле обладает энергией, поэтому рас­пространение световых волн связано с переносом энергии в про­странстве. Энергия, переносимая волнами за единицу времени через единичную площадку, перпендикулярную фазовой скорости волны, называется плотностью потока энергии S электромаг­нитной волны. В векторном виде S = [EH]. Вектор Sназывается вектором Умова-Пойнтинга. Он совпадает по направлению со скоростью волны. Среднее значение плотности потока энергии S называют интенсивностью излучения I (I=<S>).

Экспериментально доказано, что физиологическое, фото­химическое и другие действия света вызываются колебаниями электрического вектора Е, поэтому он получил название свето­вого вектора.

16. Световое давление и опыты Лебедева.

Впер­вые ги­по­те­за о су­ще­ство­ва­нии све­то­во­го дав­ле­ния была вы­ска­за­на Иоган­ном Кепле­ром в XVII веке для объ­яс­не­ния яв­ле­ния хво­стов комет при по­ле­те их вб­ли­зи Солн­ца. Макс­велл на ос­но­ве элек­тро­маг­нит­ной тео­рии света пред­ска­зал, что свет дол­жен ока­зы­вать дав­ле­ние на пре­пят­ствие. Под дей­стви­ем элек­три­че­ско­го поля волны элек­тро­ны в телах со­вер­ша­ют ко­ле­ба­ния – об­ра­зу­ет­ся элек­три­че­ский ток. Этот ток на­прав­лен вдоль на­пря­жен­но­сти элек­три­че­ско­го поля. На упо­ря­до­чен­но дви­жу­щи­е­ся элек­тро­ны дей­ству­ет сила Ло­рен­ца со сто­ро­ны маг­нит­но­го поля, на­прав­лен­ная в сто­ро­ну рас­про­стра­не­ния волны – это и естьсила све­то­во­го дав­ле­ния. Для до­ка­за­тель­ства тео­рии Макс­вел­ла необ­хо­ди­мо было из­ме­рить дав­ле­ние света. Впер­вые дав­ле­ние света из0, ме­рил рус­ский физик Петр Ни­ко­ла­е­вич Ле­бе­дев в 1900 году. При­бор Ле­бе­де­ва (Рис. 3) со­сто­ит из лег­ко­го стерж­ня на тон­кой стек­лян­ной нити, по краям ко­то­рой при­креп­ле­ны лег­кие кры­лыш­ки. Весь при­бор по­ме­щал­ся в стек­лян­ный сосуд, от­ку­да был вы­ка­чан воз­дух. Свет па­да­ет на кры­лыш­ки, рас­по­ло­жен­ные по одну сто­ро­ну стер­жень­ка. О зна­че­нии дав­ле­ния можно су­дить по углу за­кру­чи­ва­ния нити. Труд­ность точ­но­го из­ме­ре­ния дав­ле­ния света была свя­за­на с тем, что из со­су­да невоз­мож­но было вы­ка­чать весь воз­дух. При про­ве­де­нии экс­пе­ри­мен­та на­чи­на­лось дви­же­ние мо­ле­кул воз­ду­ха, вы­зван­ное неоди­на­ко­вым на­гре­вом кры­лы­шек и сте­нок со­су­да. Кры­лыш­ки невоз­мож­но по­ве­сить аб­со­лют­но вер­ти­каль­но. На­гре­тые по­то­ки воз­ду­ха под­ни­ма­ют­ся на­верх, дей­ству­ют на кры­лыш­ки, что при­во­дит к воз­ник­но­ве­нию до­пол­ни­тель­ных вра­ща­ю­щих мо­мен­тов. Также на за­кру­чи­ва­ние нити вли­я­ет неод­но­род­ный на­грев сто­рон кры­лы­шек. Сто­ро­на, об­ра­щен­ная к ис­точ­ни­ку света, на­гре­ва­ет­ся боль­ше, чем про­ти­во­по­лож­ная. Мо­ле­ку­лы, от­ра­жа­ю­щи­е­ся от более на­гре­той сто­ро­ны, пе­ре­да­ют кры­лыш­ку боль­ший им­пульс.

Так дав­ле­ние света на твер­дые тела было до­ка­за­но и из­ме­ре­но (Рис. 6–7). Зна­че­ние этого дав­ле­ние сов­па­ло с пред­ска­зан­ным дав­ле­ни­ем Макс­вел­ла.

17. Когерентность источников света. Время и длина когерентности. Лазер как источник когерентного света

18. Частичная когерентность. Пространственная и временная когерентность.

19. Способы осуществления когерентности в оптике. Метод Юнга и Френеля.

Как уже отмечалось, когерентных источников света в природе не существует. Однако когерентные световые волны можно получить, если свет, идущий от одного источника, разде­лить на две (или более) части и затем заставить их встретиться. В силу общности своего происхождения полученные лучи должны быть когерентными и при наложении интерфериро­вать. Такое разделение может быть осуществлено с помощью экранов и щелей (метод Юнга), зеркал (зеркала Френеля) и преломляющих тел (бипризма Френеля). В 1803г. английский физик Т.Юнг с помощью двух ще­лей получил на экране интерференционную картину. Его опыт заключался в следующем: источником света служила ярко ос­вещенная щель S, от которой световая волна падала на две узкие равноудаленные щели S₁ и S₂, параллельные S (рис. 2.2). Щели S₁ и S₂ можно считать когерентными источниками света, а все три упомянутые щели можно рассматривать как точечные ис­точники, свет от которых распространяется во всех направле­ниях. Волны, идущие от S₁ и S₂, накладываясь друг на друга, ин­терферируют. Интерференционная картина наблюдается на эк­ране.

Обозначим расстояние между щелями S₁ и S₂ равным d, а между щелями и экраном - l, причем l » d (рис. 2.3 а). Точка О – центр экрана, она расположена симметрично относительно ще­лей S₁ и S₂. Результат интерференции волн в произвольной точке экрана М, находящейся на расстоянии х от его центра О, должен определяться разностью хода Δ = l₂- l₁. Математический расчет дает для разности хода Δ = хd/l. В тех местах экрана, ко­торые удовлетворяют условию , образуется интерференционный максимум. Отсюда

. В тех местах экрана, где , волны “га­сят” друг друга и образуется интерференционный минимум. От­сюда

. Шириной интерференционной полосы Δх называется рас­стояние между соседними максимумами или минимумами

.

Величина Δх постоянна при заданных d, l и λ и не зависит от порядка интерференции m. Таким образом, при освещении щелей монохроматическим светом на экране наблюдается чере­дование светлых и темных полос одинаковой ширины (рис. 2.3 б). Чтобы полосы были хорошо различимы, Δх должна быть по­рядка 5 мм, тогда при λ = 500 нм отношение l/d равно 10000, т.е. выполняется условие l » d.

При освещении щелей белым светом интерференционные максимумы становятся радужными. Это происходит из-за того, что положение интерференционного максимума зависит от длины волны падающего света, а белый свет содержит в себе все цвета спектра. Максимумы коротких длин волн (фиолетовых) будут располагаться ближе к центру экрана, за ними следуют максимумы синих длин волн и т.д. до самых длинных красных (рис. 2.3 в). В середине экрана при m = 0 максимумы всех волн совпадут из-за отсутствия разности хода и получится белая по­лоса.

В настоящее время высокая степень когерентности свето­вых лучей достигается с помощью лазеров.

29.Графическое вычисление результирующей амплитуды.

амплитудаэто разница между самой высокой и самой низкой температурой. A=t(max)-t(min)

(переписать формулу с папкИ «алиби»)

58. Оптическое детектирование.

Детектирование с латинского означает открытие, обнаружение. Детектирование это преобразование электрических колебаний, в результате которого получаются колебания более низкой частоты или постоянный ток. Оптическое детектирование электрического заряда: металлические наночастицы, помещенные в раствор, могут служить также сенсорами электрического заряда, возникающего на их поверхности в результате взаимодействия с молекулами растворителя.

59. Генерация вторых гармоник, суммарной и разностной частот.

Для сред с квадратичной нелинейностью характерны трех волновые(трехчастотные, трехфотонные) взаимодействия световых волн. Поляризация среды на удвоенной частоте или на суммарной (разностной) частоте при определенных условиях могут приводить к переизлучению световой волны на соответствующих частотах. Для возбуждения поля на суммарной частоте, необходимо выполнить условие волнового синхронизма вида к3=к1+к2.процесс генерации второй гармоники относится к случаю вырожденного трехчастотного взаимодействия. С нелинейной поляризацией связаны процессы генерации разностной частоты и параметрического усиления волны.

1. Электромагнитная природа света. Структура плоских электромагнитных волн.

2. Природа света и законы его распространения интересо­вали древнегреческих ученых – Платона, Эвклида, Аристотеля еще в 400-300 гг. до нашей эры. Тогда были сформулированы законы прямолинейного распространения и отражения света, были сделаны первые попытки объяснить преломление света. К 140 г. нашей эры Птолемеем был собран большой эксперимен­тальный материал и составлены таблицы углов падения и пре­ломления световых лучей, однако найти математическую связь между ними ему не удалось. Закон преломления был открыт почти через полторы тысячи лет, в 1621 г. голландским ученым В.Снеллиусом.

3. К началу XVII в. были изобретены микроскоп, зритель­ная труба, оптические приборы в астрономии и навигации. Од­нако создание новых оптических приборов и их совершенство­вание требовало развития теоретических знаний и законов о природе света. В результате обобщения многовековых исследований к концу XVII в. в оптике сформировались две противоположные по взглядам теории света: корпускулярная «теория истечения» (И.Ньютон) и волновая (Ф.Гук и Х.Гюйгенс).

4. По теории Ньютона свет – это поток мельчайших световых частиц, корпускул, испускаемых светящимся телом и летящих прямолинейно с огромными скоростями. Движение корпускул описывалось законами классической механики.

5. Гюйгенс в своем «Трактате о свете» выдвинул совершенно иное утверждение, что свет – это упругие волны, распространяющиеся в особой среде – эфире. Борьба сторонников этих двух теорий длилась более ста лет.

6. В середине XIX в. английский физик Д.К.Максвелл обосновывает электромагнитную природу световых волн, которые в общей шкале электромагнитных волн занимают интервал длин от ~ 380 до 770 нм, что в конце XIX в. экспериментально подтверждается опытами Герца. Однако ряд явлений, открытых к тому времени – фотоэффект, тепловое излучение и др. волновая теория света объяснить не смогла. В начале ХХ в. в работах М.Планка и А.Эйнштейна были заложены основы квантовой физики, утверждающей о дискретности электромагнитного излучения и объясняющие накопившиеся противоречия.

7. Современные научные представления о природе света объединяют обе точки зрения и дают единую картину его волновых и корпускулярных свойств.

27. 3. 2. Метод зон Френеля. @

Для упрощения расчета результирующей амплитуды све­тового колебания в точке наблюдения Френель предложил ме­тод деления фронта волны на зоны. Пусть S– точечный источ­ник света, P – произвольная точка наблюдения, в которой необ­ходимо определить амплитуду Е световых колебаний. Фронт волны в опре­деленный мо­мент времени есть сфера S’ (рис. 3.3). Зоны Френеля стро­ятся таким обра­зом, что рас­стояния от краев двух соседних зон до точки на­блюдения отли­чаются на половину длины световой волны λ/2. Обозначим расстояние от точки P до волнового фронта OP = L, тогда границей централь­ной или первой зоны будут точки поверхности S’, находящиеся на расстоянии L+λ/2 от точки P. Эти точки расположены на по­верхности по окружности. Точки сферы S’, находящиеся на рас­стоянии L+2λ/2 от P, образуют границу второй кольцевой зоны, на расстоянии L+3λ/2 – гра­ницу третьей и т.д.

Обозначим Е₁ амплитуду волны, пришедшей в точку P от первой зоны, Е₂ – от второй и т.д. Колебания, приходящие в точку В от двух соседних зон, противоположны по фазе, так как их разность хода равна λ/2, они будут ослаблять друг друга. На­помним, что при прохождении волной пути в половину длины волны ее фаза меняется на противоположную. Поэтому при суммировании амплитуды нечетных зон будем брать со знаком «+», а четных – со знаком «-». В итоге результирующая ампли­туда, т.е. амплитуда колебаний от всех зон в точке P будет равна

Е = Е₁ – Е₂ + Е₃ – Е₄ +…+ Е_n.

С увеличением номера зоны амплитуда колебаний моно­тонно убывает, так как увеличивается расстояние от зоны до точки P и угол α между нормалью к поверхности зоны и на­прав­лением на точку наблюдения, поэтому по абсолютной вели­чине Е₁ > Е₂ > Е₃ > Е₄ >…> Е_n.

Из-за того, что число зон n очень велико (например, для λ= 500 нм и L = 10 см n = 80000), амплитуды двух соседних зон мало отличаются друг от друга по величине и с большой степе­нью точности можно предположить, что

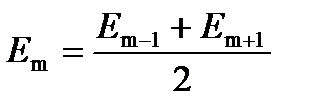. Если представить амплитуду любой не­четной зоны, например Е₁ как 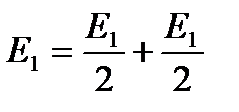, то выражение для результирующей амплитуды запишется в виде

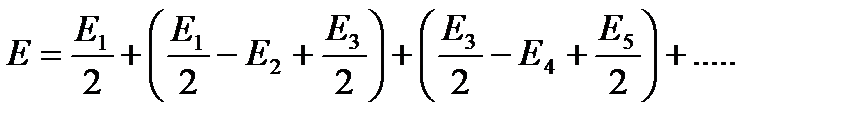
Согласно вышеприведенным рассуждениям все выраже­ния в скобках обращаются в нуль и Е ≈ Е₁/2. Результирующая амплитуда светового колебания от всей волновой поверхности в точке наблюдения равна половине амплитуды, приходящей от одной центральной зоны. Если на пути волны поставить непро­зрачный экран, оставляющий открытой только центральную зону Френеля, то амплитуда светового колебания в точке P бу­дет равняться Е₁, т.е. возрастет в два раза. Если экран открывает две зоны, их амплитуды будут «гасить» друг друга и в точке P будет наблюдаться минимум интенсивности. Если открыты три зоны, третья зона останется не скомпенсированной и в точке P будет наблюдаться максимум, и т.д. Таким образом, если на волновой поверхности открыто нечетное число зон Френеля, в точке наблюдения будет светло, если четное – темно. Если ме­жду волновой поверхностью и точкой P поставить специальную пластинку, которая закрывала бы все четные (или нечетные) зоны, то интенсивность в точке P резко возрастает. Такая пла­стинка называется зонной и действует подобно собирающей линзе.

Различают дифракцию Френеля – это дифракция в сходящихся или расходящихся лучах и дифракцию Фраунго­фера – в параллельных лучах. Разберем эти случаи более под­робно.

23. Применение явлений интерференции. Диэлектрические отражающие слои и просветление оптики.

Применение интерференции.

Перечислим важнейшие применения интерференции:

1. Измерение длин с очень большой точностью; это по­зволило дать легко воспроизводимое и достаточно точное опре­деление едини­цы длины - метра, в зависимости от длины волны оранжевой линии криптона. Интерференционные компараторы позволяют сравнивать размеры до 1 метра с точностью до 0,05 мкм; меньшие размеры могут быть измерены с еще большей точностью. Такая высокая точность обусловлена тем, что изме­нение разности хода на десятую долю длины волны заметно смещает интерференционные полосы.

2. На явлении интерференции основано действие боль­шого количества оптических приборов под общим названием интерферометры, которые используются для различных изме­рений. В оптикомеханической промышленности интерферо­метры используются для контроля качества оптических систем и контроля поверхности отдельных оптических деталей. В метал­лообрабатывающей промышленности – для контроля чистоты обработки металлических поверхностей. Изучение и контроль полировки зеркальных поверхностей (для этого применяется так называемый интерферометр Линника) проводится с точностью до сотых долей длины волны.

3. С использованием явления интерференции проводится определение ряда важнейших величин, характеризующих ве­щества: коэффициента расширения твердых тел (дилатометры), пока­зателя преломления газообразных, жидких и твердых тел (рефракто­метры) и т.п. Интерференционные дилатометры по­зволяют зафиксировать удлинение образца на 0,02 мкм.

4. Широко распространены интерференционные спектро­скопы, применяемые для исследования спектрального состава излучения различных веществ.

5. Посредством интерференции поляризованных лучей проводиться определение величин внутренних напряжений в различных деталях (метод фотоупругости).

24. Двулучевые многолучевые интерферометры.

Интерферометр – измерительный прибор, действие которого основано на интерференции волн. Оптические интерферометры применяются для измерения оптических длин волн спектральных линий, показателей преломления прозрачных сред, абсолютных и относительных длин объектов, угловых размеров звёзд и пр., для контроля качества оптических деталей и их поверхностей и т.д. Интерферометры различаются методами получения когерентных волн и тем, какая величина непосредственно измеряется. По числу интерферирующих пучков света оптические интерферометры можно разделить на многолучевые и двулучевые. Многолучевые интерферометры применяются главным образом как интерференционные спектральные приборы для исследования спектрального состава света. Двулучевые интерферометры используются и как спектральные приборы, и как приборы для физических и технических измерений.

30. Дифракция на круглом отверстии, круглом экране и на прямолинейном крае экрана.