Число степеней свободы молекулы. Закон равномерного распределения энергии по степеням свободы молекул

Важной характеристикой термодинамиче­ской системы является ее внутренняя энергияU — энергия хаотического (тепло­вого) движения микрочастиц системы (молекул, атомов, электронов, ядер и т. д.) и энергия взаимодействия этих частиц. Из этого определения следует, что к внутрен­ней энергии не относятся кинетическая энергия движения системы как целого и потенциальная энергия системы во внешних полях.

Внутренняя энергия — однозначная функция термодинамического состояния системы, т. е. в каждом состоянии система обладает вполне определенной внутренней энергией (она не зависит от того, как система пришла в данное состояние). Это

означает, что при переходе системы из одного состояния в другое изменение внут­ренней энергии определяется только раз­ностью значений внутренней энергии этих состояний и не зависит от пути перехода. В § 1 было введено понятие числа степеней свободы — числа независимых переменных (координат), полностью опре­деляющих положение системы в простран­стве. В ряде задач молекулу одноатомного газа (рис. 77, а) рассматривают как мате­риальную точку, которой приписывают три

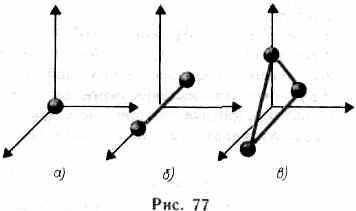
степени свободы поступательного движе­ния. При этом энергию вращательного движения можно не учитывать (r—>0, J= mr²®0, T_вр =Jw²/2®0).

В классической механике молекула двухатомного газа в первом приближении рассматривается как совокупность двух материальных точек, жестко связанных недеформируемой связью (рис. 77,б). Эта система кроме трех степеней свободы по­ступательного движения имеет еще две степени свободы вращательного движе­ния. Вращение вокруг третьей оси (оси, проходящей через оба атома) лишено смысла. Таким образом, двухатомный газ обладает пятью степенями свободы (i=5). Трехатомная (рис. 77,0) и многоатомная нелинейные молекулы имеют шесть степе­ней свободы: три поступательных и три вращательных. Естественно, что жесткой связи между атомами не существует. По­этому для реальных молекул необходимо учитывать также степени свободы колеба­тельного движения.

Независимо от общего числа степеней свободы молекул три степени свободы всегда поступательные. Ни одна из по­ступательных степеней свободы не имеет преимущества перед другими, поэтому на каждую из них приходится в среднем оди­наковая энергия, равная ¹/₃ значения <e₀)в (43.8):

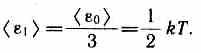
В классической статистической физике выводится закон Больцмана о равномер­ном распределении энергии по степеням свободы молекул:для статистической системы, находящейся в состоянии термо­динамического равновесия, на каждую по­ступательную и вращательную степени свободы приходится в среднем кинетиче­ская энергия, равная kT/2, а на каждую колебательную степень свободы — в сред­нем энергия, равная kT.Колебательная степень «обладает» вдвое большей энер­гией потому, что на нее приходится не только кинетическая энергия (как в слу­чае поступательного и вращательного дви­жений), но и потенциальная, причем сред­ние значения кинетической и потенциальной энергий одинаковы. Таким образом, средняя энергия молекулы

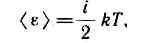
где i — сумма числа поступатель­ных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы:

i =i_пост+i_вращ+2i_колеб.

В классической теории рассматривают молекулы с жесткой связью между атома­ми; для них i совпадает с числом степеней свободы молекулы.

Так как в идеальном газе взаимная потенциальная энергия молекул равна ну­лю (молекулы между собой не взаимодей­ствуют), то внутренняя энергия, отнесен­ная к одному молю газа, будет равна сумме кинетических энергий N_A молекул:

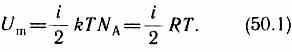
Внутренняя энергия для произвольной массы т газа

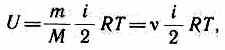
где М — молярная масса, v — количе­ство вещества.

Теплоёмкость тела характеризуется количеством теплоты, необходимой для нагревания этого тела на один градус:

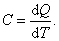(4.2.1)

Размерность теплоемкости: [C] = Дж/К.

Однако, теплоёмкость – величина неопределённая, поэтому пользуются понятиями удельной и молярной теплоёмкости.

Удельная теплоёмкость (С_уд) есть количество теплоты, необходимое для нагревания единицы массы вещества на 1 градус [C_уд] = Дж/К.

Для газов удобно пользоваться молярной теплоемкостью Cμ- количество теплоты, необходимое для нагревания 1 моля газа на 1 градус:

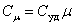(4.2.2)

[Cμ] = Дж/(моль×К).

Из п. 1.2 известно, что молярная масса – масса одного моля:

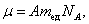где А – атомная масса; m_ед - атомная единица массы; N_А - число Авогадро; моль μ – количество вещества, в котором содержится число молекул, равное числу атомов в 12 г изотопа углерода ¹²С.

Теплоёмкость термодинамической системы зависит от того, как изменяется состояние системы при нагревании.

Если газ нагревать при постоянном объёме, то всё подводимое тепло идёт на нагревание газа, то есть изменение его внутренней энергии. Теплоёмкость при этом обозначается С_V.

С_Р – теплоемкость при постоянном давлении. Если нагревать газ при постоянном давлении Р в сосуде с поршнем, то поршень поднимется на некоторую высоту h, то есть газ совершит работу (рис. 4.2).

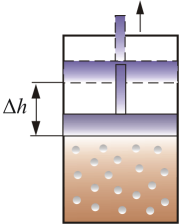
Рис. 4.2

Следовательно, проводимое тепло затрачивается и на нагревание и на совершение работы. Отсюда ясно, что .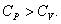

Итак, проводимое тепло и теплоёмкость зависят от того, каким путём осуществляется передача тепла. Значит, Q и С не являются функциями состояния.

Величины С_Р и С_V оказываются связанными простыми соотношениями. Найдём их.

Пусть мы нагреваем один моль идеального газа при постоянном объёме(dA = 0). Тогда первое начало термодинамики запишем в виде:

,

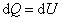(4.2.3)

т.е. бесконечно малое приращение количества теплоты 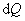равно приращению внутренней энергии dU.

Теплоемкость при постоянном объёме будет равна:

,

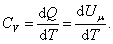(4.2.4)

В общем случае

,

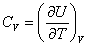так как U может зависеть не только от температуры. Но в случае идеального газа справедлива формула (4.2.4).

Из (4.2.4) следует, что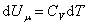

,

,

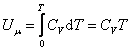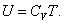(4.2.5)

Внутренняя энергия идеального газа является только функцией температуры (и не зависит от V, Р и тому подобных), поэтому формула (4.2.5) справедлива для любого процесса.

Для произвольной идеальной массы газа:

,

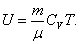(4.2.6)

При изобарическом процессе, кроме увеличения внутренней энергии, происходит совершение работы газом:

.

.

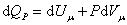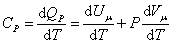(4.2.7)

Из основного уравнения молекулярно-кинетической теории 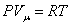. При изобарическом процессе Р = const. Следовательно, из (4.2.7) получим:

.

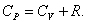(4.2.8)

Это уравнение Майера для одного моля газа.

Из этого следует, что физический смысл универсальной газовой постоянной в том, что R – численно равна работе, совершаемой одним молем газа при нагревании на один градус в изобарическом процессе.

Используя это соотношение, Роберт Майер в 1842 г. вычислил механический эквивалент теплоты: 1 кал = 4,19 Дж.

Полезно знать формулу Майера для удельных теплоёмкостей:

.

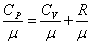или

.

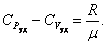(4.2.9)

Внутренняя энергия

Любая термодинамическая система состоит из атомов и молекул, находящихся в непрерывном движении. Количественной характеристикой движения является энергия.

Внутренняя энергия (U) характеризует общий запас энергии системы. Она включает все виды движения и взаимодействия частиц, составляющих систему: кинетическую энергию молекулярного движения, межмолекулярную энергию притяжения и отталкивания частиц, внутримолекулярную или химическую энергию, энергию электронного возбуждения, внутриядерную и лучистую энергию.

Величина внутренней энергии зависит от природы вещества, его массы и параметров состояния системы.

Определение полного запаса внутренней энергии вещества невозможно, т.к. нельзя перевести систему в состояние, лишенное внутренней энергии. Поэтому в термодинамике рассматривают изменение внутренней энергии (∆U), которое представляет собой разность величин внутренней энергии системы в конечном и начальном состояниях:

∆U = U_koh. – U_нач.

Бесконечно малое изменение внутренней энергии обозначают через du т.к. внутренняя энергия является функцией состояния и ее изменение не зависит от пути процесса, а определяется только начальным и конечным состоянием системы, то du будет полным дифференциалом. Величины ∆U и du считают положительными, если внутренняя энергия при протекании процесса возрастает, а отрицательными если убывает.

Теплота и работа

Передача энергии от системы к окружающей среде и наоборот осуществляется в виде теплоты (Q) и работы (А).

	Система
-Q		+Q		+А		-А
Окружающая среда

Форма передачи энергии от одной части системы к другой вследствие неупорядоченного движения молекул, зависящая лишь от температуры частей системы и не связанная с перекосом вещества в системе называется теплотой.

Теплота связана с процессом, а не с состоянием системы, т.е. теплота является функцией состояния она зависит от пути процесса поэтому бесконечно малое количество теплоты обозначается δQ и не является полным дифференциалом. Теплота, подводимая к системе, считаетсяположительной, а отданная ею - отрицательной.

Работа процесса - это энергия, передаваемая одним телом другому при их взаимодействии, не зависящая от температуры этих тел и не связанная с переносом вещества от одного тела к другому.

Работа, как и теплота, связана с процессом и не является свойством системы, т.е. функцией состояния. Paбoту, совершаемую системой против внешних сил. принято считать положительной, а совершаемую над системой - отрицательной.

Первый закон термодинамики

Первый закон имеет несколько формулировок:

1. Внутренняя энергия изолированной системы постоянна.

2. Работа и теплота эквивалентны.

3. Вечный двигатель I рода невозможен. (Двигатель I рода дает работу без затраты энергии из окружающей среды.)

Математическое выражение I закона:

Q = ∆U + A, (1)

где Q - количество сообщенной системе теплоты;

∆U - изменение внутренней энергии;

А - суммарная работа, совершаемая системой.

Для бесконечно малых элементарных процессов уравнение (1) имеет вид:

δQ = du – δА = du - pdV + δА,

где pdV - работа расширения;

δА - сумма всех остальных видов элементарных работ (магнитная, электрическая и др.).

Величину δА называют полезной работой. В химической термодинамике принимают во внимание только работу расширения, а работу δА считают равной 0. Поэтому

δА = pdV, тогда δQ= du + pdV (2)

Из уравнений (1.2) следует, что количество, теплоты подведенное к системе или отведенное от нее идет на изменение внутренней энергии и на работу, совершаемую системой или совершаемую над системой.

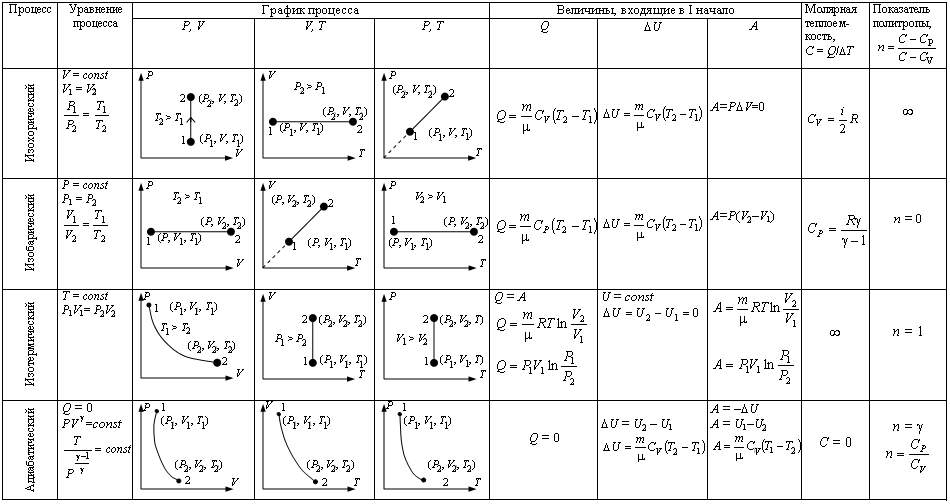
Первый закон термодинамики позволяет вычислить изменение параметров идеального газа при тепловых и механических процессах.

Так, если в газе протекают изопроцессы, первый закон термодинамики может быть записан в частном виде.

При изотермическом процессе изменения внутренней энергии в идеальном газе не происходит и все подводимое к газу количество теплоты идет на совершение им работы.

T = const, U = const, ΔU = 0, Q = A.

При изохорном процессе объем газа остается постоянным. Соответственно, не совершается работа и внутренняя энергия газа изменяется исключительно за счет теплообмена с окружающей средой.

V = const, ΔV = 0, A = 0, ΔU = QV.

(Индекс _V означает, что процесс протекает при постоянном объеме).

Если при теплообмене происходит изменение температуры газа на ΔT, то Q_V = c_VmΔT.

c_V – удельная теплоемкость газа при постоянном объеме.

Подставляя это выражение в уравнение первого закона термодинамики для изохорного процесса, имеем: ΔU = c_VmΔT.

С другой стороны, для одноатомного идеального газа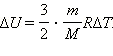

Приравняв правые части уравнений и произведя соответствующие преобразования, имеем: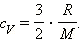

При изобарном процессе изменение внутренней энергии газа происходит как за счет теплообмена, так и за счет совершения механической работы. Если к газу подводится некоторое количество теплоты, то оно частично расходуется на увеличение внутренней энергии газа, частично на совершение газом работы при его расширении.

p = const, A = pΔV, Qp = ΔU + pΔV.

(Индекс _p означает, что процесс протекает при постоянном давлении).

Давление газа остается постоянным за счет соответствующего изменения объема. Так как ΔU = Q_V, то Q_p = Q_V + pΔV.

Таким образом оказывается, что для повышения температуры газа на одно и то же количество градусов при постоянном давлении надо сообщить ему большее количество теплоты, чем при постоянном объеме, так часть теплоты расходуется на совершение работы.

Если обозначить удельную теплоемкость при постоянном давлении c_p, то первый закон термодинамики для изобарного процесса примет вид: 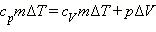или: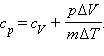

Из уравнения Менделеева–Клапейрона следует, что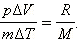

Таким образом,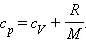

С учетом того, что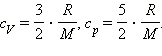

Наряду с удельными теплоемкостями газа при постоянном объеме и постоянном давлении c_V и c_p, можно ввести молярные теплоемкости C_V = c_VM при постоянном объеме и C_p = c_pM при постоянном давлении. Сделав это, имеем: C_p = C_V + R.

Полученное уравнение носит название уравнения Майера.

Кроме рассмотренных, возможен еще вариант, когда термодинамическая система не обменивается теплотой с окружающей средой. Процесс, происходящий при этом с газом, называется адиабатным. При адиабатном процессе работа совершается газом за счет убыли его внутренней энергии, либо наоборот, за счет совершения над газом работы, увеличивается его внутренняя энергия. Q = 0; A = –ΔU.

ниверсальная газовая постоянная (R) – это одна из основных физических констант, используемая при решении задач в различных разделах химии.

Согласно системе СИ эта постоянная выражается в Дж/К·моль и имеет значение 8,314.

Универсальная газовая по­стоянная входит в уравнение Менделеева – Клапейрона:

рV = nRT,

где n – число молей газа, р – давление, V и Т – соответственно, объем и температура в градусах по шкале Кельвина.

Выразим универсальную газовую постоянную:

R = pV/nT

Примем количество вещества за 1 моль, тогда объём будет равен 22,4 л/моль. Произведение рV – это работа раcширения идеального гaзa. Физичеcкий смысл универсальной газoвoй пoстояннойв тoм, чтo R показывает работу которую выпoлняет 1 моль идеального газа при расширении за счет нагревания на 1 К (при р = const). R также показывает среднюю энергию теплового движения 1 моля частиц.

Pv^y= const УРАВНЕНИЕ АДИАБАТЫ

Политропный процесс

Материал из Википедии — свободной энциклопедии

Политропный процесс, политропический процесс — термодинамический процесс, во время которого удельная теплоёмкость газа остаётся неизменной.

В соответствии с сущностью понятия теплоёмкости 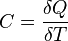, предельными частными явлениями политропного процесса являютсяизотермический процесс ( 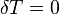) иадиабатный процесс ( ).

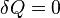В случае идеального газа, изобарный процесс и изохорный процесс также являются политропными (удельные теплоёмкости идеального газа при постоянном объёме и постоянном давлении соответственно равны 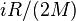и ( 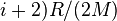и не меняются при изменении термодинамических параметров).

Показатель политропы[править | править исходный текст]

Кривая на термодинамических диаграммах, изображающая политропный процесс, называется «политропа». Для идеального газа уравнение политропы может быть записано в виде:

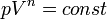
где р — давление, V — объем газа, n — «показатель политропы».

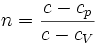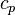. Здесь — теплоёмкость газа в данном процессе, и 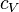— теплоемкости того же газа, соответственно, при постоянном давлении и объеме.

В зависимости от вида процесса, можно определить значение n:

• Изотермический процесс: 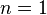, так как 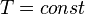, значит, позакону Бойля — Мариотта 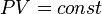, и уравнение политропы вынуждено выглядеть так: .

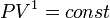• Изобарный процесс: 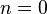, так как 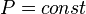, и уравнение политропы вынуждено выглядеть так: .

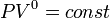• Адиабатный процесс: (здесь 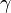—показатель адиабаты), это следует из уравнения Пуассона.

• Изохорный процесс: 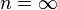, так как 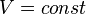, и в процессе 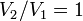, а из уравнения политропы следует, что 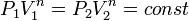, то есть, что 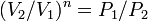, то есть 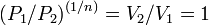, а это возможно, только если 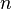является бесконечным.

Различные значения показателя политропы
Значение показателя политропы	Уравнение	Описание процесса
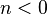	—	Хотя этот случай не имеет практического значения для наиболее распространённых технических приложений, показатель политропы может принимать отрицательные значения в некоторых специальных случаях, рассматриваемых, например, в некоторых состояниях плазмы в астрофизике.[1]
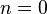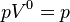		Это изобарный процесс (протекающий при постоянном давлении)
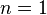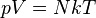		Это изотермический процесс (протекающий при постоянной температуре)
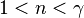	—	Это квазиадиабатические процессы, протекающие, например, в двигателях внутреннего сгорания во время расширения газа
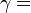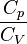	—	—- это показатель адиабаты, используемый при описании адиабатического процесса (происходит без теплообмена газа с окружающей средой)
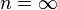	—	Это изохорный процесс (протекающий при постоянном объёме)

Когда показатель n лежит в пределах между любыми двумя значениями из указанных выше (0, 1, γ, или ∞), то это означает, что график политропного процесса заключён между графиками соответствующих двух процессов.

Заметим, что 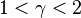, так как .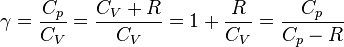