Мощность, развиваемая силой F

Единица работы

1 джоуль — работа, совершаемая силой, равной 1 Н на пути 1 м.

9.2. Мощность

Ф изическая величина, характеризующая скорость совершения работы.

Связь вектора момента силы и момента импульса

Продифференцируем (10) по времени:

(14)

Т.к. полюс неподвижен, то первое слагаемое равно нулю (т.к. первая производная перемещения по времени равна скорости). Тогда коллинеарны, а произведение коллинеарных векторов равно нулю.

Поэтому (15)

Согласно II закону Ньютона , (16)

значит (15) будет иметь вид:

или (17)

Кинетическая энергия и работа при вращательном движении.

Мысленно разобьем тело на малые частицы с массами m₁,m₂, …,m_nтак, чтобы линейные скорости материальных точек составляющих эти частицы можно было считать одинаковыми. Расстояния этих частиц от оси вращения, соответственно равныr₁,r₂, …,r_n, а скорости -v₁,v₂, …,v_n. Кинетическая энергия каждой частицы будет а всего тела:

Заменим линейную скорость v_i ее выражением через угловую v_i = ωr_i.

.

Так как угловая скорость для всех точек тела одинакова, т.е. ω=const, то

Выражение , стоящее в скобках, есть сумма моментов инерции частиц тела, т.е. момент инерции J, и тогда вырaжение для кинетической энергии вращательного движения примет вид

E= J∙ω² /2,

Если тело участвует в двух движениях одновременно - в поступательном со скоростью vи вращательном со скоростью ω, то его полная кинетическая энергия равна

Работа внешней силы постоянной величины при вращении равна ΔA= т.е. равна произведению момента внешней силы на угол поворота . В общем случаеdA=Mdφи работа будет

Если М=const, тоA=M∙φ. Эта работа затрачивается на изменение кинетической энергии вращающегося тела

Механические колебания

Автоколебания— свободные колебания, поддерживаемые внеш­ним источником энергии, включение которого в нужные моменты времени осуществляет сама колеблющаяся система (например, колебания маятника часов).

Параметрические колебания — это колебания, в процессе которых происходит периодическое изменение какого-либо параметра системы (например, раскачивание качелей: приседая в крайних положениях и выпрямляясь в среднем положении, человек, находящийся на качелях, изменяет момент инерции качелей).

Различные по своей природе колебания обнаруживают много общего: они подчиняются одним и тем же закономерностям, описываются одними и теми же уравнениями, исследуются одними и теми же методами. Это дает возможность создать единую теорию колебаний.

Простейшими из периодических колебаний

являются гармонические колебания.

Гармонические колебания- это колебания, в процессе совершения которых значения физических величин изменяются с течением времени по закону синуса или косинуса. Большинство колебательных процессов описываются этим законом или может быть приставлено в виде суммы гармонических колебаний.

2. Периодическиминазываются колебания, при которых происходит точное повторение процесса через равные промежутки времени.

Периодом периодических колебаний называется минимальное время, через которое система возвращается в первоначальное

х — колеблющаяся величина (например, сила тока в цепи, состояние и начинается повторение процесса. Процесс, происходящий за один период колебаний, называется «одно полное колебание».

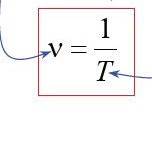
периодических колебаний называется число полных колебаний за единицу времени (1 секунду) — это может быть не целое число.

Т — период колебаний Период — время одного полного колебания.

Чтобы вычислить частоту v, надо разделить 1 секунду на время Т одного колебания (в секундах) и получится число колебаний за 1 секунду или координата точки) t — время

Гармоническое колебание

Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса.

График гармонического колебания

График устанавливает зависимость смещения тела со временем. Установим к пружинному маятнику карандаш, за маятником бумажную ленту, которая равномерно перемещается. Или математический маятник заставим оставлять след. На бумаге отобразится график движения.

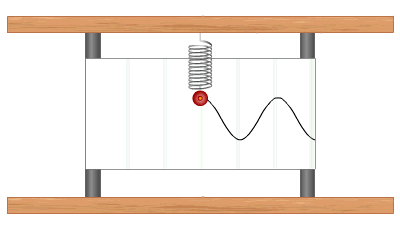
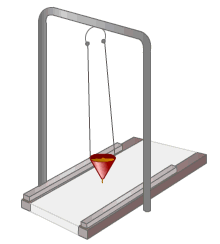
Графиком гармонического колебания является синусоида (или косинусоида). По графику колебаний можно определить все характеристики колебательного движения.

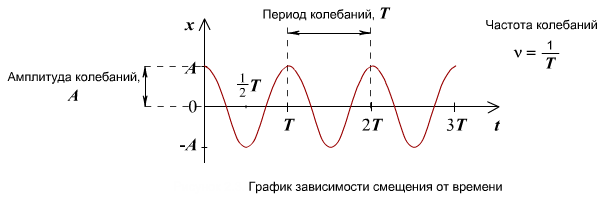
Уравнение гармонического колебания

Уравнение гармонического колебания устанавливает зависимость координаты тела от времени

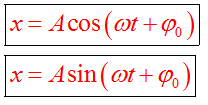
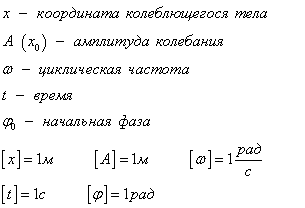
График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой .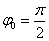

Изменение скорости и ускорения при гармоническом колебании

Не только координата тела изменяется со временем по закону синуса или косинуса. Но и такие величины, каксила, скорость и ускорение, тоже изменяются аналогично. Сила и ускорение максимальные, когда колеблющееся тело находится в крайних положениях, где смещение максимально, и равны нулю, когда тело проходит через положение равновесия. Скорость, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия - достигает максимального значения.

Вынужденные колебания.

Резонанс

В целом ряде случаев возникает необходимость создания систем, совершающих незатухающие колебания. Получить незатухающие колебания в системе можно, если компенсировать потери энергии, воздействуя на систему периодически изменяющейся силой.

Пусть

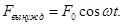
Запишем выражение для уравнения движения материальной точки, совершающей гармоническое колебательное движение под действием вынуждающей силы.

По второму закону Ньютона:

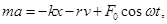
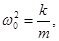
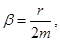
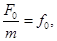
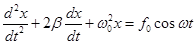(1)

- дифференциальное уравнение вынуж­денных колебаний.

Сложение гармонических колебаний одного направления и одинаковой частоты. Биения. Разложение сложного колебания в ряд Фурье. Спектральный анализ. Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу.

Внутренняя энергия

Любая термодинамическая система состоит из атомов и молекул, находящихся в непрерывном движении. Количественной характеристикой движения является энергия.

Внутренняя энергия (U) характеризует общий запас энергии системы. Она включает все виды движения и взаимодействия частиц, составляющих систему: кинетическую энергию молекулярного движения, межмолекулярную энергию притяжения и отталкивания частиц, внутримолекулярную или химическую энергию, энергию электронного возбуждения, внутриядерную и лучистую энергию.

Величина внутренней энергии зависит от природы вещества, его массы и параметров состояния системы.

Определение полного запаса внутренней энергии вещества невозможно, т.к. нельзя перевести систему в состояние, лишенное внутренней энергии. Поэтому в термодинамике рассматривают изменение внутренней энергии (∆U), которое представляет собой разность величин внутренней энергии системы в конечном и начальном состояниях:

∆U = U_koh. – U_нач.

Бесконечно малое изменение внутренней энергии обозначают через du т.к. внутренняя энергия является функцией состояния и ее изменение не зависит от пути процесса, а определяется только начальным и конечным состоянием системы, то du будет полным дифференциалом. Величины ∆U и du считают положительными, если внутренняя энергия при протекании процесса возрастает, а отрицательными если убывает.

Теплота и работа

Передача энергии от системы к окружающей среде и наоборот осуществляется в виде теплоты (Q) и работы (А).

	Система
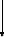-Q		+Q		+А		-А
Окружающая среда

Форма передачи энергии от одной части системы к другой вследствие неупорядоченного движения молекул, зависящая лишь от температуры частей системы и не связанная с перекосом вещества в системе называется теплотой.

Теплота связана с процессом, а не с состоянием системы, т.е. теплота является функцией состояния она зависит от пути процесса поэтому бесконечно малое количество теплоты обозначается δQ и не является полным дифференциалом. Теплота, подводимая к системе, считаетсяположительной, а отданная ею - отрицательной.

Работа процесса - это энергия, передаваемая одним телом другому при их взаимодействии, не зависящая от температуры этих тел и не связанная с переносом вещества от одного тела к другому.

Работа, как и теплота, связана с процессом и не является свойством системы, т.е. функцией состояния. Paбoту, совершаемую системой против внешних сил. принято считать положительной, а совершаемую над системой - отрицательной.

Первый закон термодинамики

Первый закон имеет несколько формулировок:

1. Внутренняя энергия изолированной системы постоянна.

2. Работа и теплота эквивалентны.

3. Вечный двигатель I рода невозможен. (Двигатель I рода дает работу без затраты энергии из окружающей среды.)

Математическое выражение I закона:

Q = ∆U + A, (1)

где Q - количество сообщенной системе теплоты;

∆U - изменение внутренней энергии;

А - суммарная работа, совершаемая системой.

Для бесконечно малых элементарных процессов уравнение (1) имеет вид:

δQ = du – δА = du - pdV + δА,

где pdV - работа расширения;

δА - сумма всех остальных видов элементарных работ (магнитная, электрическая и др.).

Величину δА называют полезной работой. В химической термодинамике принимают во внимание только работу расширения, а работу δА считают равной 0. Поэтому

δА = pdV, тогда δQ= du + pdV (2)

Из уравнений (1.2) следует, что количество, теплоты подведенное к системе или отведенное от нее идет на изменение внутренней энергии и на работу, совершаемую системой или совершаемую над системой.

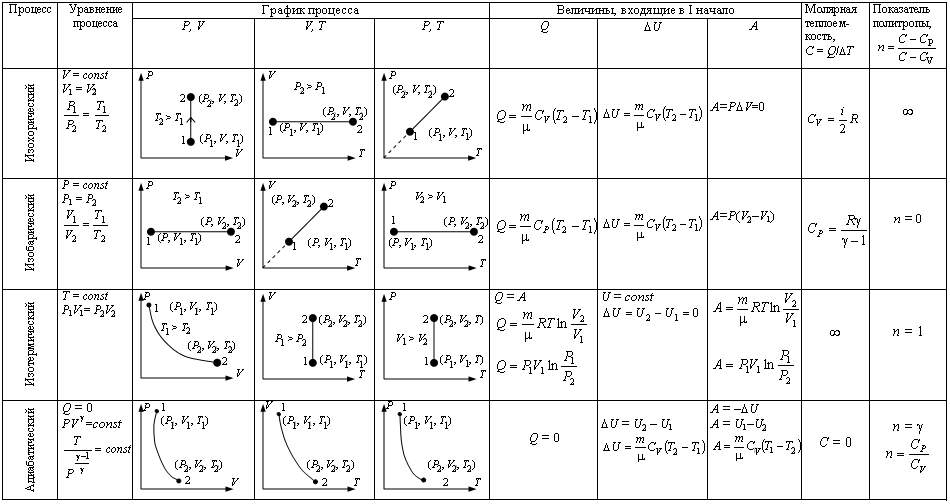
Первый закон термодинамики позволяет вычислить изменение параметров идеального газа при тепловых и механических процессах.

Так, если в газе протекают изопроцессы, первый закон термодинамики может быть записан в частном виде.

При изотермическом процессе изменения внутренней энергии в идеальном газе не происходит и все подводимое к газу количество теплоты идет на совершение им работы.

T = const, U = const, ΔU = 0, Q = A.

При изохорном процессе объем газа остается постоянным. Соответственно, не совершается работа и внутренняя энергия газа изменяется исключительно за счет теплообмена с окружающей средой.

V = const, ΔV = 0, A = 0, ΔU = QV.

(Индекс _V означает, что процесс протекает при постоянном объеме).

Если при теплообмене происходит изменение температуры газа на ΔT, то Q_V = c_VmΔT.

c_V – удельная теплоемкость газа при постоянном объеме.

Подставляя это выражение в уравнение первого закона термодинамики для изохорного процесса, имеем: ΔU = c_VmΔT.

С другой стороны, для одноатомного идеального газа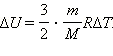

Приравняв правые части уравнений и произведя соответствующие преобразования, имеем: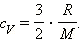

При изобарном процессе изменение внутренней энергии газа происходит как за счет теплообмена, так и за счет совершения механической работы. Если к газу подводится некоторое количество теплоты, то оно частично расходуется на увеличение внутренней энергии газа, частично на совершение газом работы при его расширении.

p = const, A = pΔV, Qp = ΔU + pΔV.

(Индекс _p означает, что процесс протекает при постоянном давлении).

Давление газа остается постоянным за счет соответствующего изменения объема. Так как ΔU = Q_V, то Q_p = Q_V + pΔV.

Таким образом оказывается, что для повышения температуры газа на одно и то же количество градусов при постоянном давлении надо сообщить ему большее количество теплоты, чем при постоянном объеме, так часть теплоты расходуется на совершение работы.

Если обозначить удельную теплоемкость при постоянном давлении c_p, то первый закон термодинамики для изобарного процесса примет вид: 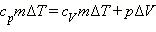или: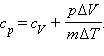

Из уравнения Менделеева–Клапейрона следует, что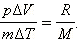

Таким образом,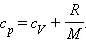

С учетом того, что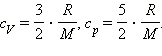

Наряду с удельными теплоемкостями газа при постоянном объеме и постоянном давлении c_V и c_p, можно ввести молярные теплоемкости C_V = c_VM при постоянном объеме и C_p = c_pM при постоянном давлении. Сделав это, имеем: C_p = C_V + R.

Полученное уравнение носит название уравнения Майера.

Кроме рассмотренных, возможен еще вариант, когда термодинамическая система не обменивается теплотой с окружающей средой. Процесс, происходящий при этом с газом, называется адиабатным. При адиабатном процессе работа совершается газом за счет убыли его внутренней энергии, либо наоборот, за счет совершения над газом работы, увеличивается его внутренняя энергия. Q = 0; A = –ΔU.

ниверсальная газовая постоянная (R) – это одна из основных физических констант, используемая при решении задач в различных разделах химии.

Согласно системе СИ эта постоянная выражается в Дж/К·моль и имеет значение 8,314.

Универсальная газовая по­стоянная входит в уравнение Менделеева – Клапейрона:

рV = nRT,

где n – число молей газа, р – давление, V и Т – соответственно, объем и температура в градусах по шкале Кельвина.

Выразим универсальную газовую постоянную:

R = pV/nT

Примем количество вещества за 1 моль, тогда объём будет равен 22,4 л/моль. Произведение рV – это работа раcширения идеального гaзa. Физичеcкий смысл универсальной газoвoй пoстояннойв тoм, чтo R показывает работу которую выпoлняет 1 моль идеального газа при расширении за счет нагревания на 1 К (при р = const). R также показывает среднюю энергию теплового движения 1 моля частиц.

Pv^y= const УРАВНЕНИЕ АДИАБАТЫ

Политропный процесс

Материал из Википедии — свободной энциклопедии

Политропный процесс, политропический процесс — термодинамический процесс, во время которого удельная теплоёмкость газа остаётся неизменной.

В соответствии с сущностью понятия теплоёмкости 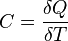, предельными частными явлениями политропного процесса являютсяизотермический процесс ( 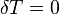) иадиабатный процесс ( ).

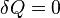В случае идеального газа, изобарный процесс и изохорный процесс также являются политропными (удельные теплоёмкости идеального газа при постоянном объёме и постоянном давлении соответственно равны 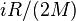и ( 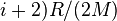и не меняются при изменении термодинамических параметров).

Показатель политропы[править | править исходный текст]

Кривая на термодинамических диаграммах, изображающая политропный процесс, называется «политропа». Для идеального газа уравнение политропы может быть записано в виде:

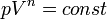
где р — давление, V — объем газа, n — «показатель политропы».

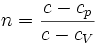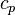. Здесь — теплоёмкость газа в данном процессе, и 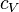— теплоемкости того же газа, соответственно, при постоянном давлении и объеме.

В зависимости от вида процесса, можно определить значение n:

• Изотермический процесс: 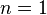, так как 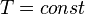, значит, позакону Бойля — Мариотта 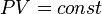, и уравнение политропы вынуждено выглядеть так: .

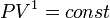• Изобарный процесс: 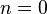, так как 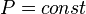, и уравнение политропы вынуждено выглядеть так: .

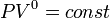• Адиабатный процесс: (здесь 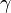—показатель адиабаты), это следует из уравнения Пуассона.

• Изохорный процесс: 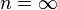, так как 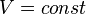, и в процессе 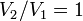, а из уравнения политропы следует, что 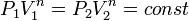, то есть, что 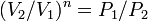, то есть 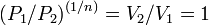, а это возможно, только если 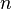является бесконечным.

Различные значения показателя политропы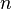
Значение показателя политропы	Уравнение	Описание процесса
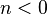	—	Хотя этот случай не имеет практического значения для наиболее распространённых технических приложений, показатель политропы может принимать отрицательные значения в некоторых специальных случаях, рассматриваемых, например, в некоторых состояниях плазмы в астрофизике.[1]
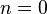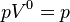		Это изобарный процесс (протекающий при постоянном давлении)
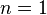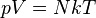		Это изотермический процесс (протекающий при постоянной температуре)
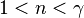	—	Это квазиадиабатические процессы, протекающие, например, в двигателях внутреннего сгорания во время расширения газа
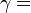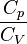	—	—- это показатель адиабаты, используемый при описании адиабатического процесса (происходит без теплообмена газа с окружающей средой)
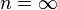	—	Это изохорный процесс (протекающий при постоянном объёме)

Когда показатель n лежит в пределах между любыми двумя значениями из указанных выше (0, 1, γ, или ∞), то это означает, что график политропного процесса заключён между графиками соответствующих двух процессов.

Заметим, что 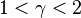, так как .

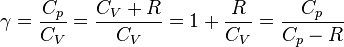Величина

Рис. 8

кристаллах титаната бария смещение ионов происходит в направлении ребер исходной кубической ячейки. Поэтому существует шесть возможных направлений спонтанной поляризации – по два взаимно противоположных направления вдоль ребер кубической ячейки. Отсюда вытекает взаимная направленность электрических моментов доменов – домены ориентированы под углами 90⁰С и 180⁰С. Рис.8 иллюстрирует схему расположения доменов в кристалле титаната бария. В поликристаллических образцах по причине хаотичности монокристаллических блоков хаотичны и направления электрических моментов доменов.

1. П оляризация образца во внешнем электрическом поле проходит несколько стадий. При малых внешних полях (областьIна рис.9) происходит обратимое смещение границ доменов. Домены, энергия которых меньше во внешнем поле ( ), т.е. , увеличиваются, а домены с - уменьшаются.

В

Рис. 9

областиIIпроисходит необратимое скачкообразное смещение границ доменов. К концу областиIIостаются только домены с энергетически выгодной ориентацией электрических моментов во внешнем поле.

В области IIIнаблюдается процесс поворота электрических моментов доменов по направлению электрического поля.

Область IVсоответствует насыщению, когда электрические моменты доменов ориентированы по направлению внешнего поля.

1. При уменьшении электрического поля после достижения насыщения должен был бы возникать обратный процесс. Но это оказывается невозможным. Дезориентация доменов связана с образованием доменов с новыми направлениями поляризованности за счет энергии теплового движения и последующим их ростом. Вероятность этого процесса невелика и определяется

Поэтому наблюдается запаздывание изменения поляризованности кристалла при уменьшении внешнего электрического поля, т.е. возникает гистерезис. Для достижения состояния с Р=0 необходимо создание внешнего поля, способствующего дезориентационному процессу и равного коэрцитивной силе.

Гистерезис (от греч. hysteresis - отставание, запаздывание) , явление, которое состоит в том, что физическая величина, характеризующая состояние тела (например, намагниченность) , неоднозначно зависит от физические величины, характеризующей внешние условия (например, магнитного поля) . Гистерезис наблюдается в тех случаях, когда состояние тела в данный момент времени определяется внешними условиями не только в тот же, но и в предшествующие моменты времени. Неоднозначная зависимость величин наблюдается в любых процессах, т. к. для изменения состояния тела всегда требуется определённое время (время релаксации) и реакция тела отстаёт от вызывающих её причин. Такое отставание тем меньше, чем медленнее изменяются внешние условия Однако для некоторых процессов отставание при замедлении изменения внешних условий не уменьшается. В этих случаях неоднозначную зависимость величин называется гистерезисной, а само явление – Гистерезис

Электрическим током называется направленное (упорядоченное) движение электрических зарядов (рис.13.1). Сами эти частицы называются носителями тока.

Ток может идти в твёрдых телах, жидкостях и газах. Если среда является проводником с большим количеством свободных электронов, то течение электрического тока осуществляется за счёт дрейфа этих электронов. Дрейф электронов в проводниках, не связанный с перемещением вещества, называют током проводимости. К току проводимости относится упорядоченное движение электронов в проводниках, ионов в электролитах, электронов и дырок в полупроводниках, ионов и электронов в газах. Упорядоченное перемещение электрических зарядов, связанное с перемещением в пространстве заряженного тела, называют конвекционным током.

За направление тока принят дрейф положительных зарядов (электроны проводимости всегда движутся в направлении, противоположном направлению тока (от «+» к «-»)). Это может показаться неудобным, но зато теперь не нужно различать направление тока в проводнике и электростатического поля, вызывающего этот ток: эти направления всегда совпадают.

Сила тока – скалярная величина, равная отношению количества электричества dq, которое за время dt переносится через данное сечение проводника, ко времени dt:

(13.1)

Постоянным током называют электрический ток, сила и направление которого с течением времени не изменяются. Для постоянного тока

где q - электрический заряд, проходящий за время t через поперечное сечение проводника.

Единица силы тока – ампер (А).

Определим скорость, с которой осуществляется дрейф электронов в проводнике с током.

Путь за время Δt через сечение проводника S прошло N электронов с суммарным зарядом Δq = Nе. Если скорость направленного движения электронов равна υ, то за время Δt все они окажутся в пределах участка длиной ℓ = υ Δt и объёмом V=Sℓ. Таким образом,

(13.2)

выразив здесь число носителей тока через их концентрацию (N = nV= nSℓ)

Отношение силы тока І к площади поперечного сечения проводника S, перпендикулярного направленню тока – есть векторная величинаназываемая плотностью тока.

(13.3)

Тогда скорость электронов в проводнике можно записать , отсюда

Плотность тока может быть вычислена по формуле

j = ne‹υ› (13.4)

Таким образом, плотность тока в проводнике пропорциональна концентрации свободных электронов в нём и скорости их движения.

Вектор j направлен вдоль направления тока, т.е. совпадает с направлением упорядоченного движения положительных зарядов.

Сила тока сквозь произвольную поверхность S определяется как поток вектора j, т.е.

(13.5)

где dS = n∙dS (n = единичный вектор нормали к площадке dS, составляющей с вектором j угол α ).

Электрическое поле постоянного тока называется стационарным. В отличии от электростатического поля стационарное электрическое поле создаётся движущимися зарядами. Однако распределение этих зарядов в проводнике с постоянным током не меняется со временем: на место уходящих электрических зарядов непрерывно приходят новые. Поэтому электрическое поле, создаваемое этими зарядами, оказывается почти таким же, как и поле неподвижных зарядов.

Отличаются же они тем, что электростатическое поле внутри проводника отсутствует, в то время как стационарное поле постоянных токов существует и внутри проводников (иначе по ним не шёл бы ток).

Если в проводнике создать электрическое поле и не принять мер для его поддержания, то, как было уже установлено, перемещение носителей заряда приведет очень быстро к тому, что поле внутри проводника исчезнет и, следовательно, ток прекратиться. Для того чтобы поддерживать ток достаточно долго, нужно от конца проводника с меньшим потенциалом (носители тока предполагаются положительными) непрерывно отводить приносимые сюда заряды, а к концу с большим потенциалом непрерывно их подводить. Т.е. необходимо осуществить круговорот зарядов, при котором они двигались бы по замкнутому пути (13.2). Циркуляция вектора напряженности электростатического поля, как известно равна нулю. Поэтому в замкнутой цепи наряду с участками, на которых положительные заряды движутся в сторону убывания потенциала, должны иметься участки, на которых перенос положительных зарядов происходит в направлении возрастания потенциала, т.е. против сил электростатического поля. Перемещение, зарядов на этих участках возможно лишь с помощью сил не электростатического происхождения, называемых сторонними силами.

Таким образом, для поддержания тока необходимы сторонние силы, действующие либо на всем протяжении цепи, либо на отдельных ее участках. Они могут быть обусловлены химическими процессами, диффузией носителей заряда в неоднородной среде или через границу двух разнородных, веществ, электрическими (но не электростатическими) полями, порожденными меняющимися во времени магнитными полями и т.д.

Например, в гальванических элементах и аккумуляторах происхождение сторонних сил – химическое. В генераторах электрического тока сторонние силы – это силы Лоренца, действующие со стороны магнитного поля.

Устройства, обеспечивающие возникновение и действие сторонних сил, называют источниками тока. В этих устройствах происходит разделение разноимённых зарядов. Под действием сторонних сил электрические заряды внутри источника тока движутся в направлении, противоположном действию сил электрического поля. В результате этого на полюсах источника тока поддерживается постоянная разность потенциалов.

Подобно тому, как насос сообщает энергию воде, поднимая её вверх, источник тока сообщает энергию заряженным частицам. Как для работы насоса, поднимающего воду, так и для работы источника тока необходима энергия. В зависимости от типа источника тока, в нём происходит преобразование механической, внутренней или ещё какой-либо энергии в электрическую. В зависимости от вида энергии, которая внутри источника тока преобразуется в электрическую энергию, различают механические, химические, тепловые источники тока.

Сторонние силы совершают работу по перемещению электрических зарядов.

Физическая величина, определяемая работой, совершаемой сторонними силами при перемещении единичного положительного заряда, называется электродвижущей силой (э.д.с.) ε, действующей в цепи.

Сторонняя сила F_ст, действующая на заряд q₀, может быть выражена как

F_ст = E_ст q₀,

где E_ст – напряжённость поля сторонних сил. Работа же сторонних сил по перемещению заряда q₀ на замкнутом участке цепи равна

(13.6)

Разделив на q₀, получим выражение для э.д.с., действующей в цепи:

(13.7)

т.е. эдс, действующая в замкнутой цепи, может быть определена как циркуляция вектора напряжённости поля сторонних сил. ЭДС, действующая на участке 1-2, равна

На заряд q₀ помимо сторонних сил действует также силы электростатического поля F_э = E q₀. Таким образом, результирующая сила, действующая в цепи на заряд q₀, равна

F =F_ст + F_э = q₀(Е_ст + E_э) (13.8)

Рисунок – 13.3

Работа, совершаемая результирующей силой над зарядом q₀ на участке 1-2, равна

(13.9)

Используя выражения и , можем записать

А₁₂ = q₀ε₁₂ + q₀ (φ₁-φ₂) (13.10)

Для замкнутой цепи работа электростатических сил равна нулю, поэтому в данном случае А₁₂ = q₀ε₁₂

Напряжением U на участке 1-2 называется физическая величина, определяемая работой, совершаемой суммарным полем кулоновских и сторонних сил при перемещении положительного единичного заряда на данном участке цепи.

U₁₂ = ε₁₂ + (φ₁-φ₂) (13.11)

Напряжение на участке цепи.

Под напряжением на некотором участке электрической цепи понимают разность потенциалов между крайними точками этого участка.

На рис. 13 изображен участок цепи, на котором есть резистор сопротивлением 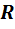и нет ЭДС. Крайние точки этого участка обозначены буквами a и b. Пусть ток течет от точки a к точке b.

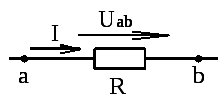
Рис. 13. Участок электрической цепи

На участке без ЭДС ток течет от более высокого потенциала к более низкому. Следовательно, потенциал 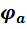точки a выше потенциала 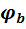точки bна величину, равную произведению тока 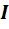на сопротивление :

.

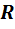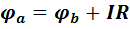В соответствии с определением, напряжение между точками a и b

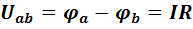.(8)

Другими словами, напряжение на резисторе равно произведению тока, протекающего по резистору, на величину сопротивления этого резистора.

В электротехнике разность потенциалов на концах резистора принято называть либо «напряжением на резисторе», либо «падением напряжения». В литературе встречаются оба этих определения.

Рассмотрим теперь вопрос о напряжении на участке цепи, содержащем не только резистор, но и источник ЭДС.

На рис. 14 а и б показаны участки некоторых цепей, по которым протекает ток 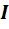.. Найдем напряжение между точками a и c для этих участков.

а) б)

Рис. 14. Участки электрической цепи

По определению

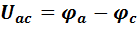.(9)

Выразим потенциал точки a через потенциал точки c. При перемещении от точки c к точке b (рис. 14,а) идем встречно ЭДС 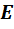, поэтому потенциал точки b оказывается меньше, ч