Теоретические основы массопередачи.

В массообмене участвуют 3 вещества:

1.Распределяющее-фаза. Ф_у (y-пар, газ)

2.Распределяющая - фаза Ф_х (х-жидкость, тв.тело)

3. Распределяющее вещество М – вещество, которое переходит из одной фазы в другую.

Особенности массообменных процессов.

1.Процесс происходит при непосредственном контакте фаз.

2.Процесс обратимый.

3.В процессе ректификации фазы Ф_х и Ф_у обмениваются компонентами, а во всех остальных массообменных процессах фазы Ф_х и Ф_у являются инертными носителями.

Способы выражения состава фаз.

1. Ф_х - жидкая или твердая фаза

2. Ф_у - паровая или газовая фаза

3.А, В, С,….N- компоненты системы

4.g_а, g_в, g_с,…g_N – массы компонентов фазы Ф_х, кг

5.g_а, g_в, g_с,…g_N- массы компонентов фазы Ф_у, кг

6. М_а, М_в, М_с,…М_N-молекулярные массы компонентов

7. Р_а, Р_в, Р_с,… Р_N-упругости паров чистых компонентов

8. Р_а, Р_в, Р_с,…Р_N-парциальные давления компонентов

9. Р_общ- общее давление

Диффундирующее в пределах фазы вещество перемещается от точки с большей концентрацией к точке с меньшей концентрацией, и в расчетах движущую силу процессов массопереноса выражают приближенно через разность концентраций, подобно тому, как в процессах теплопереноса её выражают разностью температур.

Обычно количественный состав фаз выражают:

1.а – массовые проценты- % мас, в Ф_х

в– массовые проценты- % мас, в Ф_у

а _i = 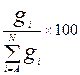в _i=

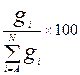
2.Массовые доли: кг/кг

= а _i /100 - в фазе Ф_х = в _i/100 - в фазе Ф_у

3.Мольные доли: кмоль/кмоль

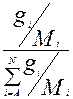x_i = y_i =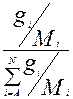

4.Относительные мольные доли :

X- 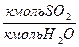- в Ф_х Y- 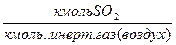-в Ф_у

5.Относительные массовые доли:

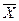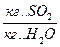- - в Ф_{х 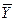-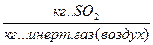} -в Ф_у

6.Объемная мольная концентрация:

С_х- 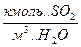С_y -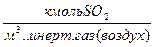

7.Объемная массовая концентрация

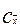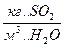_- - в Ф_{х -}

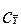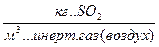
8.Состав газовых смесей часто выражают через парциальные давления компонентов.

Равновесие между фазами.

Процесс перехода вещества из одной фазы в другую (например, из газовой в жидкость) происходит до установления динамического равновесия.

Скорость перехода вещества из газа в жидкость прямо пропорциональна его концентрации:

w=m_y y

Скорость обратного процесса:

w=m_x x

При достижении динамического равновесия скорости выравниваются:

m_y y=m_x x

Уравнение равновесия:

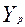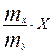= =m_yx X

y_p= y* - равновесная концентрация

m_yx - константа фазового равновесия ( коэффициент распределения)

Графическое изображение линий равновесия

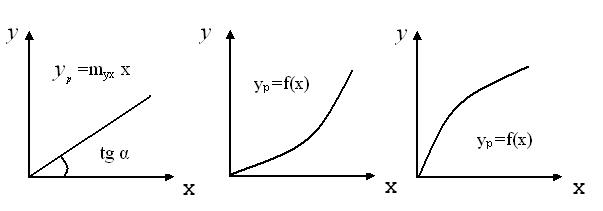
Идеальный случай Реальный Реальный

m_x x =tg α Абсорбция Ректификация,

абсорбция экстракция

Если концентрации фаз выражены в одной и той же размерности, то «m» величина безразмерная, если нет, то будет иметь соответствующую размерность

Уравнение равновесия необходимо для определения направления протекания процесса и движущей силы.

Материальный баланс

Разберем на процессе абсорбции.

Пример: Пусть идет поглощение SO₂ из воздуха водой. Рассмотрим схему движения потоков в противоточном аппарате.

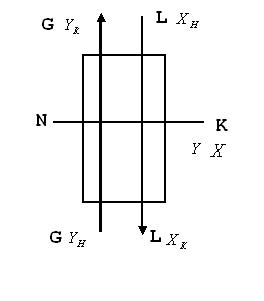
В аппарат поступают фазы G и L.

Расход фазы G является постоянным – это количество газовой инертной фазы (воздух), кмоль/с. L- жидкостная фаза (вода), расход постоянный, кмоль/с.

Y_Н, Y_К, X_Н, X_К –концентрация SO₂ в газе и жидкости на входе и выходе из аппарата.

Дано: G, Y_Н, Y_К, X_Н=0, X_К

Определить: расход жидкости L и количество абсорбированного вещества M.

Запишем уравнение материального баланса по поглощаемому веществу для сечения N-K, в котором текущие концентрации составляют Y и X.

-GdY= LdX=dM

-GdY- баланс по поглощаемому компоненту, знак (-) означает, что концентрация вещества в газовой фазе уменьшается.

Какая получается размерность:

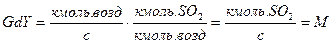
Запишите: интегрируем всегда по ходу газа, по ходу жидкости

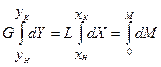- и получим:

M=G (Y_Н - Y_К) =L (X_К - X_Н )

Из этого уравнения получим соотношения между массовыми потоками распределяющих фаз

G= L 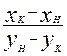L= G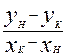

Удельный расход абсорбента найдем из соотношения:

l =L/G =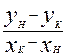

Уравнение рабочей линии

1^ый случай- противоток.

Запишем уравнение материального баланса по поглощаемому компоненту по ходу газа до произвольно выбранного сечения N-K.

-GdY= LdX проинтегрируем:

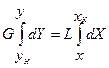- и получим:

G (Y_Н - Y) =L (X_К – X )

Решим это уравнение относительно Y:

Y= Y_Н –L/G(X_К – X ) = Y_Н – l (X_К – X )

Это уравнение рабочей линии для противотока, отображающее изменение рабочих концентраций в произвольном сечении аппарата N-K.

Уравнение рабочей линии имеет вид:

Y= Ax +B

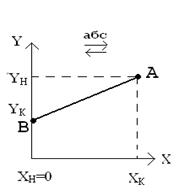Графическое изображение рабочей линии.

Как видно из уравнения рабочей линии, на диаграмме в координатах X-Y, рабочая линия представляет собой прямую с наклоном к оси абсцисс под углом , тангенс которого равен l .

т.А с координатами Y_Н ,X_К . т.В (X_Н,Y_К)

2^ой случай – прямоток:

Запишем уравнение материального баланса по поглощаемому компоненту от входа до сечения N-K

-GdY= LdX

-

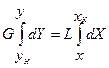
G (Y_Н - Y) =L (X_К – X )

Y = Y_Н – l (X_К – X )

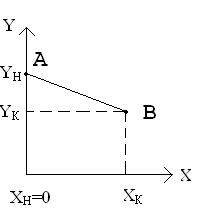
т.А (Y_Н, X_Н) т.В (Y_К, X_К)

Точки, лежащие на рабочей линии, отражают рабочие концентрации, лежащие на равновесной линии - равновесные концентрации.