Мера Жордана. Двойной интеграл по измеримой по Жордану области. Свойства двойного интеграла. Теорема о среднем. Вычисление двойного интеграла

1. Мера Жордана. Критерий измеримости

Пусть 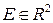- ограниченное множество, А- прямоугольник, ,

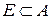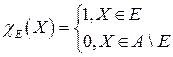- характеристическая функция множества E.

Определение.Множество Е измеримо по Жордану или имеет объем 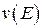, если 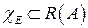, при этом .

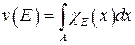Это определение на самом деле не зависит от выбора прямоугольника А и в этом смысле является корректным. Пусть

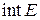- множество всех внутренних точек множества Е,

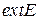- внешность множества Е или внутренность дополнения множества Е,

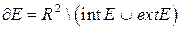-граница множества Е.

Теорема. (Критерий измеримости по Жордану). Е измеримо по Жордану тогда и только тогда, когда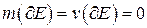

Доказательство.Е измеримо по Жордану .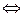

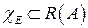
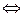
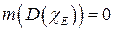Докажем равенство 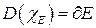, т.е. что множество точек разрыва характеристической функции совпадает с границей множества.

Рассмотрим три случая для точек прямоугольника А

1. Точка 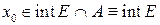. Тогда существует окрестность 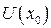такая, что .

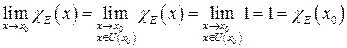2. Точка 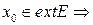существует окрестность 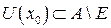такая, что

.

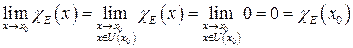3. Точка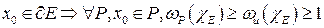

.

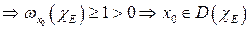2. Двойной интеграл по измеримой по Жордану области. Достаточное условие интегрируемости

Пусть 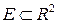ограниченное множество, А- прямоугольник,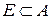

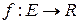-ограниченная функция,

.

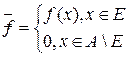Определение.Функция 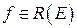, если 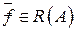. При этом .

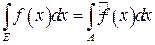Можно показать, что это определение корректное, т.е. не зависит от выбора прямоугольника А.

Отметим, в частности, что по этому определению .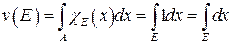

Теорема. (Достаточное условие интегрируемости по Риману). Если 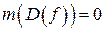и Е измеримо по Жордану, то функция .

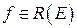Доказательство.Достаточно доказать следующее включение

.

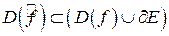Пусть 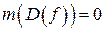, Е измеримо по Жордану, т.е. .

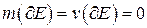Пусть 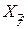- точка непрерывности функции 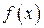, , 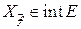т.е существует окрестность : .

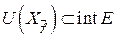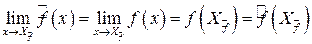Отсюда следует, что 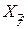- точка непрерывности функции .

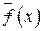Пусть 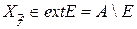, т.е. существует окрестность 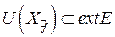: 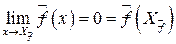. Это также точка непрерывности .

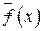Искомое включение доказано. Теорема доказана.

3. Свойства двойного интеграла. Теорема о среднем

Будем предполагать, что все множества является измеримыми по Жордану.

Отметим следующие свойства интеграла Римана.

1. Если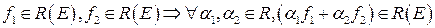

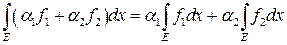
(линейность интеграла Римана по функциям).

2. Если .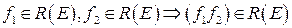

3. Если 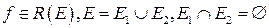, то

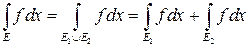
(линейность интеграла Римана по множествам).

Доказательство.

,

, .

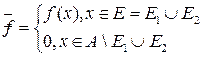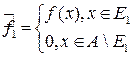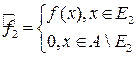Имеем .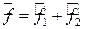

Отсюда .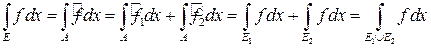

4. Если .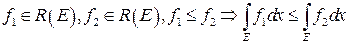

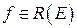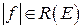5. Если , то и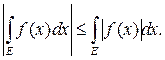

Следует из неравенств .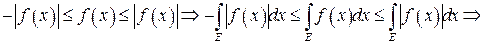

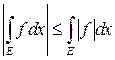6. Если 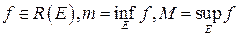, то .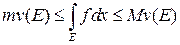

Следует из неравенств

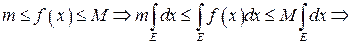
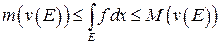
7. Если 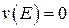, 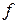ограничена на Е, то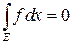

Следует из неравенств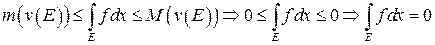

Теорема о среднем. Если Е компактное и связное множество в 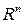, , 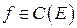то существует точка : .

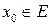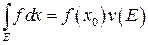Если 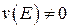, то число 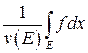называется средним значением функции на множестве .

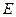Доказательство.Из непрерывности и компактности вытекает что существуют точки .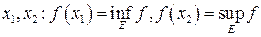

Из свойства 6 следует, что 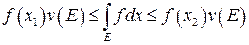. Если

.

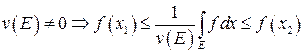По теореме о промежуточных значениях из непрерывности 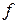и связности Е следует, что существует точка : .

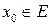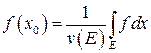Теорема доказана.

4. Вычисление двойного интеграла

Применим теорему Фубини к вычислению двойного интеграла по произвольной области.

Пусть 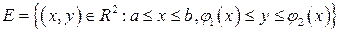, 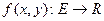. Такая область называется правильной при проектировании ее на ось 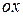Аналогично, область 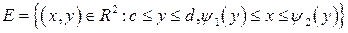называется правильной при проектировании ее на ось .

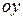С помощью теоремы Фубини сведем вычисление двойного интеграла по правильной области при проектировании на ось 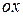к повторному интегралу. Пусть ,

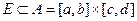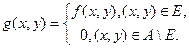
По определению интеграла и теореме Фубини

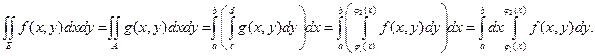
ЛЕКЦИЯ 4