Критерий Лебега существования двойного интеграла по прямоугольной области

Иванов В.И.

профессор, д.ф.-м.н.

КОНСПЕКТ ЛЕКЦИЙ

по дисциплине

Математический анализ

(Часть 3)

Направление подготовки: 010400 «Прикладная математика и информатика»

Профиль подготовки: «Прикладная математика и информатика»

Форма обучения: очная

Тула 2013 г.

Рассмотрено на заседании кафедры

протокол № 1 от 02 сентября 2013 г.

Зав. кафедрой________________В.И. Иванов

СОДЕРЖАНИЕ

ЛЕКЦИЯ 1. Двойной интеграл по прямоугольной области. Два определения. Их эквивалентность. Критерий интегрируемости Римана. Вычисление интеграла путем сведения к повторному. 4

ЛЕКЦИЯ 2. Критерий Лебега существования двойного интеграла по прямоугольной области. 8

ЛЕКЦИЯ 3. Мера Жордана. Двойной интеграл по измеримой по Жордану области. Свойства двойного интеграла. Теорема о среднем. Вычисление двойного интеграла. 11

ЛЕКЦИЯ 4. Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах 15

ЛЕКЦИЯ 5. Тройной интеграл, его вычисление. Замена переменных в тройном интеграле. Тройной интеграл в цилиндрических и сферических координатах. 17

ЛЕКЦИЯ 6. Механические приложения двойного и тройного интеграла. 20

ЛЕКЦИЯ 7. Криволинейный интеграл 1-го рода. Его свойства, вычисление, приложения. 21

ЛЕКЦИЯ 8. Криволинейный интеграл 2-го рода. Его физический смысл. Формула Грина. Условия независимости интеграла от пути в R². 25

ЛЕКЦИЯ 9. Площадь поверхности в R³. Поверхностный интеграл 1-го рода. Его свойства, вычисление, приложения 29

ЛЕКЦИЯ 10. Поверхностный интеграл 2-го рода. Его связь с поверхностным интегралом 1-го рода. Соленоидальное поле. Дивергенция. Теорема Гаусса-Остроградского. Потенциальное поле. 32

ЛЕКЦИЯ 11. Циркуляция. Ротор. Формула Стокса. Поток векторного поля. Условия независимости криволинейного интеграла 2-го рода от пути в R³ 35

ЛЕКЦИЯ 12. Дифференциальные векторные операции 2-го порядка. Гармоническое поле, гармонические функции. Ортогональные криволинейные координаты. Коэффициенты Ламе. Выражение оператора Лапласа в ортогональных координатах. 39

ЛЕКЦИЯ 13. Сходимость и сумма числового ряда. Свойства сходящихся числовых рядов. Необходимые условия сходимости. Критерий Коши. 42

ЛЕКЦИЯ 14. Сходимость рядов с положительными членами. Критерий сходимости. Признак сравнения. Признак Даламбера. 44

ЛЕКЦИЯ 15. Радикальный признак Коши. Признак Коши для рядов с монотонными членами. Интегральный признак Коши. 47

ЛЕКЦИЯ 16. Ряды с произвольными членами. Абсолютная и условная сходимости. Признаки Лейбница, Абеля, Дирихле. 50

ЛЕКЦИЯ 17. Условная и безусловная сходимости. Теорема Римана о перестановках условно сходящегося ряда. Критерий безусловной сходимости. Сходимость бесконечного произведения. Необходимое условие сходимости. Сведение сходимости бесконечного произведения к сходимости числового ряда. Абсолютная и условная сходимости. 53

ЛЕКЦИЯ 1

Двойной интеграл по прямоугольной области. Два определения. Их эквивалентность. Критерий интегрируемости Римана. Вычисление интеграла путем сведения к повторному

1. Двойной интеграл по прямоугольной области. Два определения

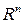Пусть -параллелепипед в (замкнутый параллелепипед с гранями параллельными координатным плоскостям), - объем параллелепипеда, функция -ограниченная.

Необходимо определить число связанное с , называемое интегралом от 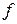по множеству : .

Для простоты все построения будем вести для . В этом случае

,

.

Пусть - множество точек ,

- разбиения отрезков ,

-разбиение прямоугольника ; под разбиением прямоугольника будем понимать и маленькие прямоугольники

.

Этих прямоугольников будет . Пусть далее

- мелкость или диаметр разбиения (максимальная диагональ прямоугольников ),

- разметка разбиения ,

размеченное разбиение.

В дальнейшем индексы у прямоугольников будем опускать, т.е будем писать .

Определим 3 типа интегральных сумм:

· ,

- интегральная сумма, отвечающая размеченному разбиению ;

· - верхняя сумма Дарбу;

· -нижняя сумма Дарбу.

Отметим следующие свойства этих сумм

1. Для любого : .

2. При измельчении разбиения (получается путем добавления новых точек на или ) верхние суммы Дарбу не увеличиваются, а нижние суммы Дарбу не уменьшаются.

3. Для любых : ,

Действительно, если измельчение как как и то .

4. Если - множество всех нижних сумм Дарбу, - множество всех верхних сумм Дарбу, то и по аксиоме непрерывности существует : .

Определение 1. - нижний интеграл Дарбу.

Определение 2. - верхний интеграл Дарбу.

5. Для любых : .

Определение 3. Первое определение интеграла Римана.

Будем говорить, что функция 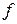интегрируема по Риману на прямоугольнике и интеграл равен числу , если существует , не зависящий от разметки , т.е для любого существует такое, что для любого разбиения и любой разметки разбиения : .

Будем писать .

Определение 4. Второе определение интеграла Римана.

Будем говорить, что функция 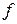интегрируема по Риману на прямоугольнике и интеграл равен числу , если .

Критерий Коши. Для того чтобы функция 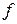была интегрируема на прямоугольнике необходимо и достаточно ,чтобы для любого существовало такое, что для любых разбиений выполняется

.

2. Эквивалентность двух определений интеграла Римана

Доказательство эквивалентности двух определений интеграла Римана будет основано на двух леммах Дарбу.

Лемма 1. .

Лемма 2. .

Теорема. Оба определения интеграла Римана является эквивалентными, т.е

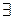
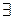
Если в смысле первого определения, то в смысле определения второго и обратно.

Доказательство.

1. . Доказательство опирается на вторую лемму Дарбу.

Если 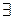и не зависит от , то : . Отсюда будет

. Поэтому

, .

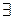
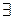
2. . Доказательство опирается на первую лемму Дарбу.

3. Критерий интегрируемости Римана

Теорема (критерий интегрируемости Римана).

, т.е 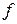интегрируема по Риману тогда и только тогда, когда .

Будем использовать запись .

Здесь - колебание функция на прямоугольнике (разность между самым большим и самым маленьким значением).

Следствие. является линейным пространством и кольцом.

Доказательство.Доказательство сводится к проверке замкнутости относительно сложения и умножения.

Для доказательства оценим колебания на прямоугольнике суммы и произведение функций.

а. .

Имеем

.

Далее .

б.

Имеем

Далее все очевидно.

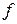Теорема. , т.е. если функция непрерывна, то она интегрируема.

Доказательство. Имеем .

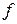Если , А- компактное, то равномерно непрерывна на А, поэтому

, такое, что , и будет .

Итак .

Отсюда, по критерию Римана .

4. Вычисление интеграла путем сведения к повторному

Вычисление двойного интеграла по прямоугольнику основано на теореме Фубини. В этом случае она выглядит следующим образом.

Теорема Фубини. Если , то для любого , и справедливы следующие равенства

Последние два интеграла называют повторными.

ЛЕКЦИЯ 2

Доказательство.

Необходимость. Пусть функция 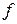непрерывна в точке . Предположим, что . Рассмотрим . Из определения получим, что существуют точки такие, что .

Кроме того, имеем . Это противоречит непрерывности функции 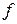в точке . Следовательно .

Достаточность. Поскольку , то для любого существует такое, что для любых имеем . Полагая , получаем непрерывность в точке то лемма.

Лемма 4. множество - ограниченное и замкнутое, т.е. компактное.

Доказательство.Так как, то - ограниченное.

Пусть - предельная точка . Покажем, что она принадлежит . Поскольку предельная точка , то существует последовательность , сходящая к . Отсюда для любого найдется , открытое, поэтому существует такое, что . Отсюда имеем , то есть

.

Лемма доказана.

Пусть - множество точек разрыва функции 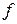на прямоугольнике А.

Лемма 5. .

Множество, которое можно представить в виде счетного объединения замкнутых множеств называется множеством типа . Итак, множество точек разрыва функции 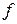- множество типа .

3. Критерий Лебега

Теорема 1. (Критерий Лебега).Ограниченная функия тогда и только тогда, когда .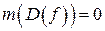

Следствие.Всякая функция, имеющая не более чем счетное множество точек разрыва интегрируемая.

Теорема 2. (Критерий интегрируемости). Ограниченная функия тогда и только тогда, когда для любого . .

Сначала выведем теорему 1 из теоремы 2. Доказательство теоремы 1.

Необходимость. Ограниченная функция по теореме 2, если для любого . .

Достаточность.

По теореме 2 имеем .

Теорема доказана.

Доказательство теоремы 2.

Необходимость . Предположим, что существует , . То есть найдется такое, что для любого набора , , но . Рассмотрим любое разбиение Т прямоугольника А на прямоугольники . Пусть -множество всех тех прямоугольников , внутри которых находится хотя бы одна точка множества . Заметим что для любого прямоугольника из колебание функции на этом прямоугольнике не меньше чем . Отсюда для любого Т Это означает, что функция не интегрируема на прямоугольнике. Получили противоречие. Значит, для любого .

Достаточность. Положим .

Так как , то его можно покрыть открытыми прямоугольниками , . Выделим из конечное подпокрытие . Рассмотрим . Оно является компактом. Для любого , .Из определения получим, что существует открытый квадрат Н такой, что колебание функции на нем меньше чем . Квадраты Н образуют открытое покрытие множества К. Выделим из него конечное покрытие V. Продолжим стороны прямоугольников, составляющих I и V до пересечения со сторонами прямоугольника А. Получим разбиение Т, для которого

.

Таким образом, .

Теорема доказана.

Следствия из критерия Лебега.

1. .

2. .

3. Пусть . Тогда .

ЛЕКЦИЯ 3

ЛЕКЦИЯ 4

ЛЕКЦИЯ 5

ЛЕКЦИЯ 6

ЛЕКЦИЯ 7

ЛЕКЦИЯ 8

Криволинейный интеграл 2-го рода. Его физический смысл. Формула Грина. Условия независимости интеграла от пути в R²

1. Криволинейный интеграл 2-го рода. Его физический смысл

Пусть 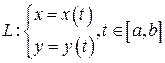- гладкая кривая,

.

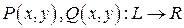Пусть 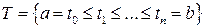- разбиение отрезка ,

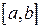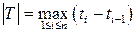- мелкость разбиения,

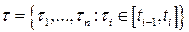- разметка разбиения.

Образуем следующую интегральную сумму:

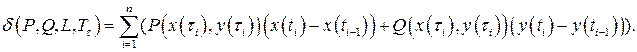Будем говорить, что для функций 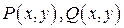существует криволинейный интеграл второго рода по кривой 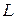в направлении возрастания параметра 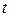(от начальной точки кривой к конечной точке), если существует 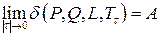, не зависящий от 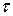, т.е.

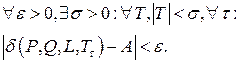
Этой интеграл имеет следующее обозначение

.

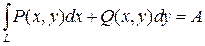Он зависит от ориентации кривой

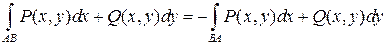
В случае замкнутой кривой различают положительную и отрицательную ориентацию: против часовой стрелки и по часовой стрелке.

Этот случай подчеркивают следующим обозначением

.

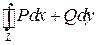Функции 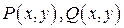в записи интеграла можно считать координатами вектора 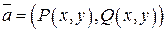. Его называют векторным полем, заданным на кривой .

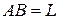Обозначим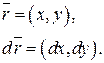

Криволинейный интеграл 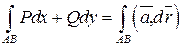определяет работу векторного (силового) поля 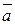вдоль кривой 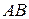в направление от точки А к точке В. Работу по замкнутой кривой часто называют циркуляцией.

2. Формула Грина

Теорема (Формула Грина).Пусть в односвязной области 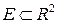задано векторное поле 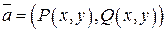таким, что функции 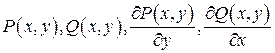- непрерывные в Е .Кривая 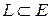, множество 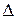, ограниченное этой кривой выпуклое . Тогда справедлива формула

.

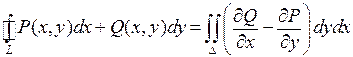Здесь кривая 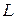обходится в положительном направлении.

Доказательство.Будем считать, что рассматриваемая область односвязная, т.е. в ней нет исключенных участков.

y

y = y₂(x)

D

A

C

B

y= y₁(x)

0 x₁ x₂ x

Если замкнутый контур имеет вид, показанный на рисунке, то криволинейный интеграл по контуру L можно записать в виде:

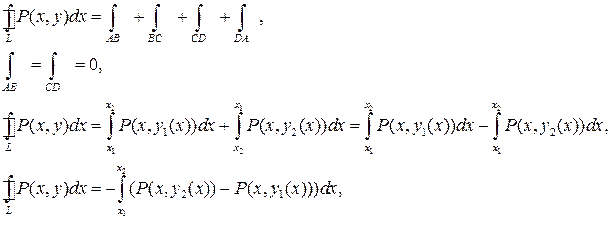
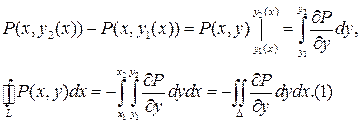
Рассуждая аналогично, для области правильной при проектировании на ось 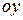, получим

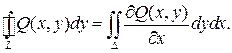(2)

Складывая (1) и (2), получим формулу Грина.

3. Условия независимости интеграла от пути в R²

Лемма.Работа векторного поля не зависит от пути тогда и только тогда, когда любая циркуляция равна 0.

Доказательство.Пусть 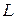произвольный замкнутый контур, точки А и В – любые точки на . Тогда

.

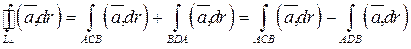Работа векторного поля не зависит от пути .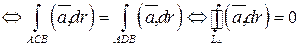

Лемма доказана.

Векторное поле 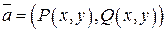называется потенциальным, если существует функция 2-х переменных 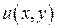- скалярное поле такое, что 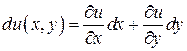,т.е .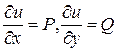

Замечание.В дифференциальных уравнениях уравнение первого порядка, записанное в дифференциалах 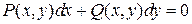называется уравнением в полных дифференциалах, если существует скалярное поле : .

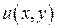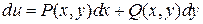В этом случае общий интеграл уравнения имеет вид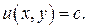

Теорема.Если в односвязной области 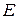функции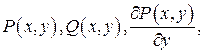 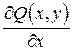непрерывны, то следующие условия эквивалентны:

1) поле 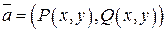- потенциальное в ;

2) 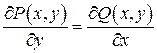в ;

3) Работа поля 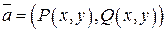в не зависит от пути.

Доказательство.Будем следовать схеме .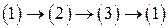

·

Поле 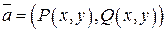- потенциальное в , поэтому 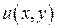-скалярное поле : 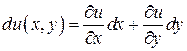, т.е.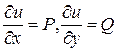

.

·

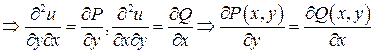Достаточно проверить, что любая циркуляция в 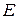равна 0.

Используем формулу Грина, получим

.

·

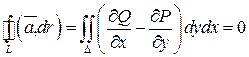Покажем, что следующее скалярное поле и есть искомый потенциал:

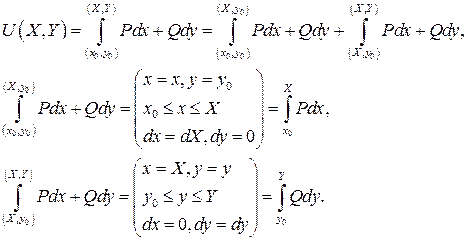
Итак,

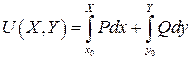
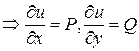
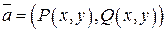-потенциальное поле в .

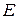ЛЕКЦИЯ 9

Площадь поверхности в R³. Поверхностный интеграл 1-го рода. Его свойства, вычисление, приложения

1. Площадь поверхности в R³

Поверхность в 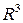задается параметрически при помощи 2 параметров

,

,

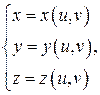
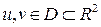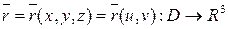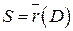- поверхность в .

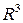Иногда поверхность задают при помощи одной функции двух переменных

.

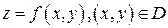Поверхность 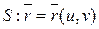называется гладкой если:

.

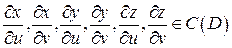Из этих частных производных можно записать матрицу Якоби нашего отображения

.

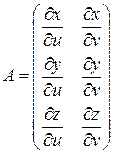Точку 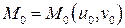назовем не особой, если ранг А в этой точке максимален и равен двум. В не особой точке векторы-столбцы являются линейно не зависимыми.

Выясним геометрический смысл этих векторов. Эти векторы 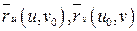- касательные векторы к линиям 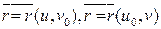на поверхности. В не особой точке эти касательные векторы не коллинеарные.

Можно показать, что все касательные векторы к кривым на поверхности, проходящие через , лежат в одной плоскости. Эта плоскость называется касательной плоскостью к поверхности в точке .

В не особой точке уравнение касательной плоскости можно записать с помощью точки и двух касательных векторов :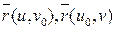

.

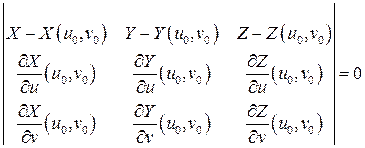Рассмотрим вектор .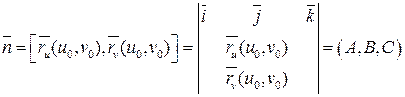

Очень часто в качестве нормального вектора будем использовать единичный нормальный вектор

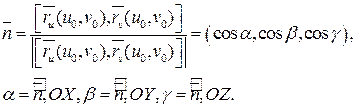
Определим первую квадратную форму на поверхности. Пусть

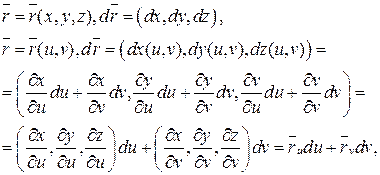
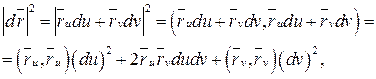
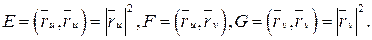
Таким образом, первая квадратичная форма на поверхности имеет вид:
.

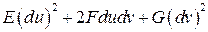Определение.Площадью гладкой поверхности 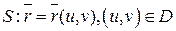, 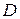-измеримо по Жордану, называется число: .

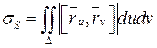Преобразуем эту формулу для площади поверхности

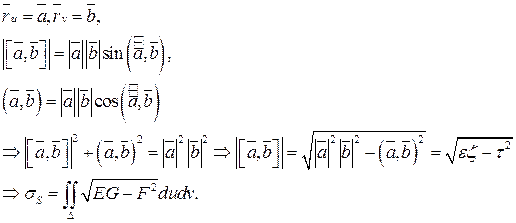
2. Поверхностный интеграл 1-го рода. Его свойства, вычисление

Пусть поверхность ,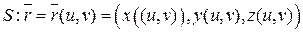

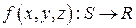- непрерывная функция.

Определение.Поверхностным интегралом первого рода по поверхности 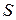от функции 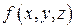называется число

.

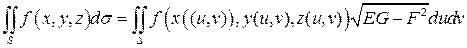Здесь 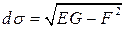- элемент площади поверхности.

Данное определение справедливо и для кусочно-гладкой поверхности, т.е. поверхности, которая может быть разбита на конечное число гладких участков.

Поверхностный интеграл первого рода сводится к некоторому двойному интегралу и для него справедливы все его свойства.

3. Приложения поверхностного интеграла 1-го рода

Геометрическое приложение: Вычисление площади поверхности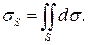

Механические приложения: Вычисление массы, статических моментов, координат центра тяжести поверхности, начиненной веществом с плотностью .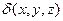

Масса: .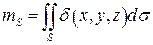

Первые статические моменты относительно координатных плоскостей:

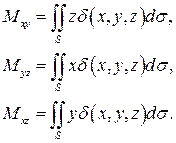
Координаты центра тяжести:

.

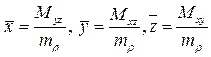Вторые статические моменты относительно координатных плоскостей:

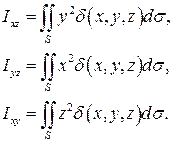
Статический момент (момент инерции) относительно начала координат:

.

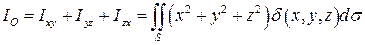ЛЕКЦИЯ 10

ЛЕКЦИЯ 11

Формула Стокса. Условия независимости криволинейного интеграла 2-го рода от пути в R³. Потенциальное поле. Циркуляция. Ротор

1. Формула Стокса

Пусть

- двусторонняя поверхность

.

Тогда множество - граница (или край) поверхности S.

Теорема (Формула Стокса). Если ориентации на 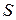и согласованы, то

Доказательство. Необходимо доказать равенство

или три равенства

Для простоты докажем первое равенство в предложении, что поверхность

.

Имеем

Что и требовать показать.

3. Потенциальное поле. Циркуляция. Ротор

Векторное поле называется потенциальным, если существует скалярное поле - потенциал такой, что

т.е. есть решение системы

Циркуляциейвекторного поля вдоль замкнутой кривой L называется криволинейный интеграл второго рода

В случае, когда векторное поле является силовым полем, циркуляция даёт величину работы этого поля вдоль кривой L.
Ротором (или вихрем) дифференцируемого векторного поля называется вектор

.

2. Условия независимости криволинейного интеграла 2-го рода от пути в R³

Лемма. Работа векторного поля в области не зависит от пути, а зависит только от начала и конца пути 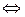любая циркуляция в E равна 0.

Доказательство. Точно такое же, как в плоском случае.

Теорема. Следующие условия эквивалентны:

1) поле потенциальное, в односвязной области E;

2) ротор в области E;

3) работа поля в E не зависит от пути.

Доказательство. Будем следовать схеме .

:

Наши рекомендации