Трубопровод с насосной подачей жидкости
Для технических гидросистем основным способом принудительного движения жидкости является применение насоса. Рассмотрим простой трубопровод, в котором насос Н подаёт жидкость из приёмного бака А в напорный бак В (рис. 6.10). Трубопровод, идущий от насоса, называют напорным. Трубопровод, по которому насос всасывает жидкость, называют всасывающим.

Рис. 6.10. Трубопровод с насосной подачей жидкости
Составим уравнение Бернулли для сечений 3 – 3 и 4 – 4 относительно плоскости сравнения 0 – 0, совпадающей с горизонтальной осью насоса. Учтём, что на выходе (сечение 3 – 3) из насоса создаётся избыточное давление, скорость течения жидкости в баке В (сечение 4 – 4) примерно равна нулю (V4 ≈ 0), давление на свободной поверхности жидкости в баке В – избыточное. Течение жидкости будем считать турбулентным, поэтому коэффициент Кориолиса для всего трубопровода α = 1. Диаметры напорного и всасывающего трубопроводов примем равными, поэтому V1 = V2 = V3 = V. Тогда уравнение Бернулли примет вид:
 , (6.9)
, (6.9)
где hн – высота нагнетания жидкости насосом в напорном трубопроводе;
h3-4 – потери напора в напорном трубопроводе.
Составим уравнение Бернулли для всасывающего трубопровода для сечений 1 – 1 и 2 – 2 относительно той же плоскости сравнения. Давление на свободной поверхности жидкости в баке А атмосферное. Давление в сечении 2 – 2 на входе в насос будет избыточным. Тогда уравнение Бернулли для давлений в избыточной системе отсчёта примет вид:
 , откуда
, откуда
 , (6.10)
, (6.10)
где hв – высота всасывания жидкости насосом.
h1-2 – потери напора во всасывающем трубопроводе.
Знак «–» при определении давления на входе в насос указывает на вакуумметрическое давление.
Полная удельная энергия жидкости в трубопроводе:
- на выходе из насоса (6.9)  ;
;
- на входе в насос (6.10)  .
.
Приращение удельной энергии жидкости в насосе для единицы её веса называется напором насоса Нн:
 ,
,
 ,
,
где Нг – полная высота подъёма жидкости насосом, называемая геометрической высотой (  ).
).
Сумма геометрической и пъезометрической высоты есть статический напор:
 .
.
Потери напора выразим через расход:
 , тогда
, тогда  .
.
Тогда напор насоса будет равен:
 , (6.11)
, (6.11)
 ,
,
где Kтр – величина сопротивления всего трубопровода.
Формула (6.11) для определения напора насоса Нн для подачи жидкости на статическую высоту Нст и преодоление гидравлических потерь, идентична формуле потребного напора трубопровода (6.4):
 . (6.12)
. (6.12)
На полученном равенстве основан метод расчёта насосного трубопровода, который заключается в построении на одном графике напорной характеристики насоса  и потребной характеристики трубопровода
и потребной характеристики трубопровода  . Точка пересечения этих характеристик называется рабочей точкой, для координат которой справедливо равенство (6.12).
. Точка пересечения этих характеристик называется рабочей точкой, для координат которой справедливо равенство (6.12).
Напор насоса Нн является функцией его объёмной подачи, то есть объёма подаваемой жидкости в единицу времени – расхода Q.
Графическое нахождение рабочей точки для турбулентного режима течения жидкости с насосной подачей изображено на рис. 6.11.

Рис. 6.11. Графическое нахождение рабочей точки для турбулентного режима течения жидкости с насосной подачей:
Нст – статический напор;  – напорная характеристика насоса;
– напорная характеристика насоса;  – потребная характеристика трубопровода; R – рабочая точка; HR и QR – напор и подача насоса в рабочей точке
– потребная характеристика трубопровода; R – рабочая точка; HR и QR – напор и подача насоса в рабочей точке
Кавитационный расчёт насоса
Для любого насоса возникновение кавитации во всасывающем патрубке приводит к ухудшению характеристик насоса, в частности, значительному снижению напора и к разрушению рабочих органов насоса. Для предупреждения возникновения кавитации абсолютное давление во входном патрубке насоса должно быть не ниже давления насыщенного пара рнп. Так как давление рнп является величиной абсолютной, а давление во входном патрубке ниже атмосферного на величину вакуумметрического давления, можно записать условие, при котором будет обеспечиваться нормальная работа насоса:
 , (6.13)
, (6.13)
где рвак – вакуумметрическое давление на входе в насос;
рнп – давление насыщенного пара при данной температуре.
Рассмотрим насос, расположенный на высоте hвс от свободной поверхности жидкости (рис. 6.12). Составим уравнение Бернулли для сечений 1 – 1 и 2 – 2 относительно плоскости сравнения 0 – 0, совпадающей со свободной поверхностью жидкости в резервуаре. Уравнение составим для давлений в абсолютной системе отсчёта, течение жидкости будем считать турбулентным (α = 1), скорость на входе в насос в сечении 2 – 2 обозначим как Vвс – скорость потока жидкости во всасывающем патрубке насоса:
 ,
,
 , (6.14)
, (6.14)
где hвс – высота всасывания;
h1-2 – потери напора во всасывающем трубопроводе;
L и d – длина и диаметр всасывающего трубопровода.

Рис. 6.12. Схема всасывающего трубопровода
Согласно (6.14), вакуумметрическая высота Нвак во всасывающем патрубке насоса определяется суммой всасывающей высоты, удельной кинетической энергией (скоростного напора) потока и гидравлических потерь во всасывающем трубопроводе:
 . (6.15)
. (6.15)
Вакуумметрическое давление рвак во входном патрубке насоса не должно превышать критического вакуумметрического давления рвак.кр, при котором возможно возникновение кавитации:
 , следовательно
, следовательно
 . (6.16)
. (6.16)
Выражение  назовём критической вакуумметрической высотой Нкр.вак. Для обеспечения нормальной работы насоса назначают некоторое превышение критической вакуумметрической высоты на величину ∆h:
назовём критической вакуумметрической высотой Нкр.вак. Для обеспечения нормальной работы насоса назначают некоторое превышение критической вакуумметрической высоты на величину ∆h:
 , (6.17)
, (6.17)
где Hдоп.вак – допустимая вакуумметрическая высота;
∆h – кавитационный запас.
Критическую вакуумметрическую высоту, при которой возникает кавитация в жидкости, определяют по результатам кавитационных испытаний насоса. Кавитационный запас ∆h составляет 20 … 30 % от критической вакуумметрической высоты:
 ,
,
 .
.
Взаимосвязь высот Нкр.вак, Ндоп.вак и кавитационного запаса ∆h представлена на рис. 6.13.

Рис. 6.13. Схема к определению высот Нкр.вак, Ндоп.вак, ∆h
Согласно выражению (6.14), вакуумметрическое давление во входном патрубке насоса зависит от высоты всасывания, диаметра трубопровода и гидравлических потерь:
 .
.
Предельная высота всасывания hвс указывается в паспортных данных насоса. Для гидроприводов автомобильной техники и машиностроительных гидроприводов характерно расположение насоса в баке, или бак располагают таким образом, что уровень жидкости в баке будет выше входного отверстия в насос. На свободной поверхности жидкости в баке может быть создано избыточное давление.
Так как давление рвак на входе в насос обратно пропорционально диаметру входного патрубка в четвёртой степени, диаметр входного отверстия в насос, как правило, больше выходного отверстия. Увеличение диаметра на входе приводит к снижению скорости течения жидкости и снижению значения вакуумметрического давления.
Для технических гидроприводов характерна малая длина всасывающего трубопровода, поэтому гидравлические потери по длине малы и практически не оказывают влияния на работу гидропривода. Местные сопротивления могут оказывать значительное влияние. В частности, установка фильтра может быть причиной значительного вакуумметрического давления. Поэтому на входе в насос устанавливают, как правило, фильтры грубой очистки.
Гидравлический удар
При быстром закрытии запорного устройства (например, задвижки или клапана) в напорном трубопроводе происходит резкое повышение давления, связанное с уменьшением скорости движения жидкости до нуля, и преобразованием кинетической энергии потока в потенциальную. Схема гидравлического удара в трубопроводе приведена на рис. 6.14. Жидкость по трубопроводу длиной L и диаметром d движется со скоростью V0, избыточное давление в трубопроводе р0 определяется высотой столба жидкости h в резервуаре, открытом в атмосферу.
При быстром закрытии затвора давление в трубопроводе повысится на величину ∆р. В результате жидкость будет сжиматься, диаметр трубопровода в результате деформации увеличится до значения d + ∆d. В трубопроводе образуется фронт ударной волны с давлением р + ∆р, перемещающейся от затвора к резервуару со скоростью С.

Рис. 6.14. Схема гидравлического удара в трубопроводе:
За фронтом ударной волны происходит выравнивание давления и скорости потока, направленного в обратную сторону - к резервуару, до начальных значений р0 и V0, стенки трубопровода и жидкость возвращаются в первоначальное состояние.
Так как жидкость движется от задвижки, происходит понижение давления на величину (– ∆р), расширение жидкости и сжатие трубопровода. После достижения фронтом волны резервуара происходит движение в прямом направлении (к задвижке) со скоростью V0 и давлением р0. При достижении задвижки возникает ситуация, соответствующая начальному моменту при закрытии затвора.
В связи с упругими свойствами жидкости и материала стенок трубопровода, а также гидравлическими потерями на трение процесс носит затухающий характер (рис. 6.15).

Рис. 6.15. Циклограмма изменения давления при гидравлическом ударе
Время цикла, при котором происходит повышение и уменьшение давления на величину ∆р, называется фазой гидравлического удара T:
 , (6.18)
, (6.18)
где L – длина трубы, по которой перемещается фронт ударной волны;
С – скорость перемещения ударной волны.
Если время закрытия задвижки tз < T, то есть трубопровод перекрывается практически мгновенно, происходит так называемый прямой гидравлический удар.
В этом случае повышение давления определяют по формуле Жуковского:
 , (6.19)
, (6.19)
 ,
,
где Еж и Ем – модуль упругости жидкости и материала трубопровода;
d – диаметр трубопровода.
Если время закрытия задвижки tз > T, в момент возвращения ударной волны через не перекрытую часть живого сечения потока успевает пройти некоторый расход жидкости со скоростью V. Кинетическая энергия потока уменьшается по сравнению с прямым ударом, и потенциальная энергия станет меньше. Такой гидравлический удар называют непрямым гидравлическим ударом. В этом случае формула Жуковского преобразуется к виду:
 , (6.20)
, (6.20)
где ∆рн – повышение давления в трубопроводе при непрямом гидроударе;
tз – время перекрытия живого сечения трубопровода.
При непрямом гидравлическом ударе величина ∆рн не зависит от скорости С распространения ударной волны. Таким образом, чтобы уменьшить повышение давления в трубопроводе, необходимо увеличить время закрытия задвижки или клапана, перекрывающего живое сечение потока в трубопроводе.
Примеры решения задач
Для сложного трубопровода, состоящего из n-го количества участков, справедливы следующие равенства:
- для последовательного соединения трубопровода (6.5)

- для параллельного соединения трубопроводов (6.6)

На равенствах (6.5) и (6.6) основан способ определения параметров сложного трубопровода - напора, расхода и геометрических параметров трубопровода. Неизвестные параметры трубопровода могут быть определены аналитически или графоаналитически, построением характеристики сложного трубопровода. Для этого необходимо выполнить следующие действия:
- представить сложный трубопровод в виде соединения простых участков;
- для каждого простого участка составить уравнение потребного напора (6.4) или гидравлическую характеристику трубопровода (6.5)
 ,
,
 .
.
С достаточной точностью можно принять:
- для ламинарного режима
 , m = 1,
, m = 1,  ,
,
где Lэкв – длина, эквивалентная всем местным гидравлическим сопротивлениям в трубопроводе;
- для турбулентного режима
 , m = 2.
, m = 2.
При аналитическом определении неизвестных параметров трубопровода составляют систему уравнений, где количество неизвестных не превышает количество уравнений, например, система уравнений для разветвлённого трубопровода (6.8).
При графоаналитическом определении неизвестных параметров необходимо построить характеристику сложного трубопровода. Для этого необходимо:
- рассчитать и построить характеристики каждого простого участка трубопровода;
- провести графическое сложение характеристик последовательных участков по оси расхода, или сложение характеристик параллельных участков по оси напора (оси ординат).
Для разветвлённого трубопровода сложение характеристик проводят по правилу сложения характеристик параллельного трубопровода.
Задачи на расчёт простого трубопровода можно разбить на три типа:
Первый тип. Даны:
- расход жидкости Q в трубопроводе;
- все геометрические размеры (длина L, диаметр d и геометрическая высота h);
- эквивалентная шероховатость труб ∆Э;
- давление или напор в конечном сечении (для всасывающих трубопроводов - в начальном);
- параметры жидкости (плотность ρ и кинематическая вязкость ν).
Местные сопротивления либо заданы коэффициентами ζм или эквивалентными длинами Lэкв, либо оцениваются по справочным данным.
Требуется найти потребный напор Нпотр.
В этом случае задачу решают в следующей последовательности:
- по известным значениям Q, d и ν находят число Рейнольдса Rе и определяют режим течения жидкости;
- при ламинарном режиме течения искомый напор определяют по формуле (6.4), где коэффициент K определяют по формуле для ламинарного режима;
- при турбулентном режиме задачу решают по той же формуле (6.4), где коэффициент K определяют по формуле для турбулентного режима. Коэффициент λ определяют по соответствующим формулам (4.6), (4.7) или (4.8) в зависимости от соотношения толщины вязкого подслоя потока δ и размера эквивалентной шероховатости ∆Э.
Второй тип. Даны: напор Нрасп, который будем называть располагаемым, так как он известен, и все величины, перечисленные в первом типе задач, кроме расхода Q. Так как число Рейнольдса в данной задаче определить нельзя, то необходимо выразить расход Q через критическое число Рейнольдса Rе = 2300 и определить Нкр, соответствующее смене режима. Сравнив Нкр и Нрасп, можно легко определить режим течения.
При ламинарном режиме задача решается просто, как и в задаче первого типа. При турбулентном режиме задача решается по формулам (6.3) и (6.4).
В уравнении (6.4) содержатся два неизвестных - расход Q и коэффициент λт, зависящие от числа Рейнольдса. Для решения задачи задают значение коэффициента λт с учётом шероховатости и определяют его по формуле Альтшуля при Rе →  :
:
 .
.
Значение коэффициента λт изменяется в небольших пределах (λт = 0,015 … 0,045).
Затем, решая уравнение (6.4), находят расход Q в первом приближении. По найденному расходу Q определяют Rе в первом приближении, а по Rе – уже более точное значение λт. Обычно бывает достаточно второго приближения.
Для решения этой же задачи графическим способом строят кривую потребного (располагаемого) напора для данного трубопровода с учётом переменности λт, то есть для ряда значений Q подсчитывают V, Rе, λт и Нпотр. Затем, построив кривую Нпотр = f(Q), и зная ординату Нпотр = Нрасп, находят соответствующую ей абсциссу, то есть находят расход Q.
Третий тип. Даны: расход Q, располагаемый напор Нрасп, и все величины, перечисленные ранее, кроме диаметра трубопровода d, который и нужно определить.
Так как число Рейнольдса определить нельзя, то выражают диаметр через критическое число Рейнольдса Rе = 2300 и определяют Нкр, соответствующее смене режима движения жидкости. Сравнивая Нкр и Нрасп, определяют режим течения.
При ламинарном режиме задача решается просто по соответствующим формулам.
При турбулентном режиме задачу решают графически. При этом задаются рядом значений диаметра d, по которым подсчитывают Нпотр. Затем строят график Нпотр= f(d) и по нему, зная Нрасп, определяют диаметр d.
Задача 6.8.1. На рисунке показан всасывающий трубопровод гидросистемы. Длина трубопровода L = 1 м, диаметр d = 20 мм, расход жидкости Q = 0,314 л/с, абсолютное давление воздуха на свободной поверхности жидкости в баке р0 = 100 кПа, высота h = 1 м, плотность жидкости (масло индустриальное при 25°С) ρ = 900 кг/м3. Коэффициент сопротивления поворота ζпов = 0,42.
Определить абсолютное давление перед входом в насос при температуре рабочей жидкости t1 = 25°С (ν = 0,2·10-4 м2/с). Определить, как изменится искомое давление в зимнее время, когда при этом же расходе температура жидкости упадет до t2 = –35°С (ν = 10·10-4 м2/с).

Рис. 6.16. Схема к задаче 6.8.1
Определим скорость течения жидкости в трубе V2 из уравнения расхода (3.2):
 = 1 м/с.
= 1 м/с.
Определим число Рейнольдса (3.15):
 = 1000.
= 1000.
Режим движения жидкости ламинарный (Re < 2300, α = 2), поэтому потери по длине hдл определим по формуле Пуазейля (4.5):
 = 0,163 м.
= 0,163 м.
Потери в местных сопротивлениях определим по формуле Вейсбаха (4.10). Для местных потерь напора при втекании в бак (внезапное сужение ζвс = 0,5, так как  ), и на повороте:
), и на повороте:
 = 0,047 м.
= 0,047 м.
Общие потери напора
 = 0,21 м.
= 0,21 м.
Составим уравнение Бернулли для сечений 1 – 1 и 2 – 2, проведя плоскость сравнения 0 - 0 по оси горизонтального участка трубы, откуда выразим абсолютное давление р2 перед входом в насос:
 , откуда
, откуда

 = 106,07 кПа.
= 106,07 кПа.
Подсчитаем потери по длине при t2 = –35°С:
 = 8,16 м.
= 8,16 м.
Общие потери напора  = 8,21 м.
= 8,21 м.
Тогда искомое давление при при t2 = –35°С:
 = 28,54 кПа.
= 28,54 кПа.
Давление на входе в сечении 2 – 2 ниже атмосферного на давление вакуума рвак = р2 – рат = 28540 – 100000 = 71,46 кПа.
Задача 6.8.2. По трубопроводу диаметром d = 10 мм и длиной L = 10 м подаётся жидкость вязкостью ν = 0,0001 м2/с под действием перепада давления ∆р = 4 МПа, плотность жидкости ρ = 1000 кг/м3. Определить режим течения жидкости в трубопроводе.
Определим расход жидкости в трубопроводе. Поскольку потери в трубопроводе будут равны разности пъезометрических высот, то с учётом формулы Пуазейля (4.5):
 , откуда
, откуда
 = 0,98 л/с.
= 0,98 л/с.
Теперь определим критический расход Qкр при критическом значении числа Рейнольдса Rе = 2300:
 , откуда
, откуда
 = 1,8 л/с.
= 1,8 л/с.
Поскольку Q < Qкр, значит, режим течения жидкости - ламинарный.
Задача 6.8.3. Определить потребный напор Нпотр, который необходимо создать в сечении 0 – 0 для подачи в бак воды плотностью ρ = 1000 кг/м3 и вязкостью ν = 0,0157 Cт, если длина трубопровода L = 80 м, его диаметр d = 50 мм, расход жидкости Q = 15 л/с, высота h = 30 м, избыточное давление в баке р0 = 0,2 МПа, коэффициент сопротивления крана ζкр = 5, поворота ζпов = 0,8, эквивалентная шероховатость внутренних стенок трубы ∆Э = 0,04 мм. Внутреннюю поверхность трубы считать гидравлически шероховатой.

Рис. 6.17.Схема к задаче 6.8.3
Составим уравнение Бернулли для сечений 0 – 0 и 1 – 1 относительно плоскости сравнения, совпадающего с сечением 0 – 0:
 ,
,
 ,
,
 .
.
Определим число Рейнольдса, воспользовавшись уравнениями (3.15) и (3.2):
 = 243420.
= 243420.
Поскольку режим течения турбулентный (α0 = 1), то потери напора по длине определим по формуле Дарси – Вейсбаха (4.3):
 .
.
Для определения потерь напора по длине определим скорость V0 течения жидкости и коэффициент гидравлического трения λ:
- скорость течения жидкости  = 7,64 м/с;
= 7,64 м/с;
- коэффициент λ по формуле Альтшуля (4.7)
 = 0,02.
= 0,02.
Тогда потери по длине  = 95,3 м.
= 95,3 м.
Местные потери напора (с учетом внезапного расширения ζр = 1) будут равны:
 = 27,4 м.
= 27,4 м.
Общие потери напора
 = 122,7 м.
= 122,7 м.
Тогда потребный напор равен:
 = 220 м.
= 220 м.
Избыточное давление, необходимое для создания Нпотр = 220 м, будет равно:
 = 2,165 МПа.
= 2,165 МПа.
Задача 6.8.4. Определить расход Q в трубе для подачи воды (вязкость ν = 0,01 Ст, плотность ρ = 1000 кг/м3) на высоту h = 16,5 м, если диаметр трубы d = 10 мм, длина L = 20 м, располагаемый напор в сечении 1 – 1 трубы перед краном Нрасп = 20 м, коэффициент сопротивления крана ζкр = 4, поворота ζпов = 1. Трубу считать гидравлически гладкой.

Рис. 6.18. Схема к задаче 6.8.4
Уравнение Бернулли для сечений 1 – 1 и 2 – 2 относительно плоскости сравнения 0 – 0, совпадающей с горизонтальной осью трубы:
 , или
, или
 .
.
Располагаемый напор Нрасп будет равен:
 ,
,
 .
.
Выразим скорость V1 через расход Q из уравнения расхода и подставим в скоростной напор  . Тогда:
. Тогда:
 .
.
Гидростатический напор в данном случае равен геометрической высоте h (Нст = h). Потери напора
 ,
,
 =
=
 =
=
 .
.
С учётом уравнения для определения располагаемого напора можно записать:
 =
=
 .
.
Предположим, что режим движения жидкости - турбулентный (α = 1, m = 2). Тогда в этом уравнении два неизвестных - Q и λт, взаимосвязь между которыми определяется зависимостью:
 ;
;
 ;
;
 .
.
Решим задачу методом последовательных приближений, задаваясь значениями коэффициента λт (λт находится в пределах 0,015 … 0,045). Пусть λт = 0,03. Тогда, выразив число Рейнольдса Rе из формулы Блазиуса (4.6) для гидравлически гладких труб, получим:
 .
.
Предположение о турбулентном режиме движении жидкости верно. Определим скорость V1 и расход Q при Rе = 12310 (λт = 0,03):
 = 1,23 м/с,
= 1,23 м/с,
 = 0,096·
= 0,096·  м3/с.
м3/с.
Тогда:
 = 4,96 м,
= 4,96 м,
что не соответствует разности  = 3,5 м.
= 3,5 м.
Примем значение λт = 0,032. Тогда:
Rе = 9509; V1 = 0,95 м/с; Q = 0,075·  м3/с,
м3/с,
 = 3,21≠ 3,5 м.
= 3,21≠ 3,5 м.
Примем значение λт = 0,0316. Тогда:
Rе = 10 000; V1 = 1 м/с; Q = 0,078·  м3/с,
м3/с,
 ,
,
что соответствует  = 3,5 м.
= 3,5 м.
Итак, методом последовательных приближений значение расхода
Q = 0,078·  м3/с.
м3/с.
Решим эту же задачу графическим методом. Для этого построим зависимость Нрасп = f(Q). Выберем ряд значений для расхода Q. Уравнение располагаемого напора представим в виде:
 ,
,
 .
.
Результаты расчётов сведём в таблицу 4.
Таблица 4
Значения параметров для построения графической зависимости Нрасп = f(Q)
Q,  , м3/с , м3/с |  , м/с , м/с | 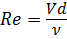 |  |  , м , м |
| 0,05 | 0,64 | 0,035 | ||
| 0,07 | 0,89 | 0,0325 | 19,34 | |
| 0,09 | 1,14 | 0,03 | 20,86 | |
| 0,11 | 1,40 | 0,029 | 22,8 | |
| 0,13 | 1,65 | 0,0278 | ||
| 0,15 | 1,91 | 0,0269 | 27,5 |

Рис. 6.19. Графическая зависимость Нрасп = f(Q)
Из построенного графика видно, что при располагаемом напоре Нрасп = 20 м расход жидкости составит Q = 0,078 л/с, что соответствует определению расхода методом подбора.
Задача 6.8.5. При каком диаметре трубопровода подача насоса составит Q = 1 л/с, если на выходе из него располагаемый напор Нрасп = 9,6 м, длина трубопровода L = 10 м, эквивалентная шероховатость ∆Э = 0,05 мм, избыточное давление в баке р1 = 30 кПа, высота h = 4 м, вязкость жидкости ν = 0,015 Ст (  м2/с), плотность ρ = 1000 кг/м3. Местными гидравлическими сопротивлениями в трубопроводе пренебречь. Учесть потери при входе в бак.
м2/с), плотность ρ = 1000 кг/м3. Местными гидравлическими сопротивлениями в трубопроводе пренебречь. Учесть потери при входе в бак.

Рис. 6.20. Схема к задаче 6.8.5
Составим уравнение Бернулли для сечений 0 – 0 и 1 – 1 относительно плоскости сравнения, совпадающей с сечением 0 – 0:
 , где
, где
- потери напора  ;
;
- коэффициент потерь  = 1, так как S2
= 1, так как S2  S1;
S1;
- располагаемый напор  ;
;
- статический напор  = 7 м.
= 7 м.
Уравнение Бернулли примет вид:
 .
.
Выразим скорость V0 течения жидкости через расход Q:
 , тогда
, тогда
 ,
,
 = 2,6 м.
= 2,6 м.
Определим режим течения жидкости. Для этого определим диаметр d трубопровода при Rе = 2300. Воспользовавшись формулой Пуазейля (4.5), сравним получаемую разность напоров с заданной Нрасп – Нст:
 = 0,37 м,
= 0,37 м,
 м
м  2,6 м.
2,6 м.
Режим течения, определяемый расходом Q =1 л/с, будет турбулентным (α0 = 1). Тогда потери напора определим по формуле:
 = 2,6 м,
= 2,6 м,
 .
.
Решим задачу графически. Для этого, задаваясь значениями диаметра d, определим разность напоров Нрасп – Нст по уравнению:
 .
.
Таблица 5
Значения параметров для построения графической зависимости
Нрасп – Нст = f(d)
| d, мм |  |  |  |
| 0,03 | 248,1 | ||
| 0,0285 | |||
| 0,0278 | 7,66 | ||
| 0,0276 | 2,36 | ||
| 0,0277 | 0,95 | ||
| 0,028 | 0,45 |
Для более точного построения графика зададим дополнительные значения диаметра d в пределах 21 … 24 мм.
| d, мм |  |  |  |
| 0,0277 | 5,7 | ||
| 0,02772 | 4,4 | ||
| 0,02768 | 3,6 | ||
| 0,02767 | 2,9 |
По полученным данным построим график Нрасп – Нст = f(d):

Рис. 6.21. График зависимости Нрасп – Нст = f(d)
При Нрасп – Нст = 2,6 м диаметр трубопровода d = 24,5 мм.
Задача 6.8.6. Трубопровод с расходом жидкости Q = 0,32 л/с в точке М разветвляется на два трубопровода: первый размерами L1 = 1,0 м и d1 = 10 мм; второй размерами L2 = 2,0 м и d2 = 8 мм. В точке N эти трубопроводы смыкаются. Во втором трубопроводе установлен фильтр, сопротивление которого эквивалентно сопротивлению в трубе длиной Lэ = 200d2. Определить расход и потери давления в каждом трубопроводе, если плотность жидкости ρ = 900 кг/м3, кинематическая вязкость ν = 1 Ст. Течение жидкости считать ламинарным.

Рис. 6.22. Схема к задаче 6.8.6
Определим расход Q1 и Q2 в каждом трубопроводе по формуле (4.5):
 ,
,
 .
.
Так как при параллельном соединении трубопроводов потери в них равны (hпот1 = hпот2), то после сокращения одинаковых величин получим:
 ,
,
 .
.
Сумма расхода в точке М в данном случае будет равна сумме расходов в параллельных трубопроводах:
 , откуда
, откуда
 = 0,0327 л/с,
= 0,0327 л/с,
 = 0,287 л/с.
= 0,287 л/с.
Потери давления:
 = 105 кПа,
= 105 кПа,
 =
=
 кПа.
кПа.
