II. Значащие и запасные цифры в числах и вычислительные операции с этими числами.
Правильная запись результатов прямых и косвенных измерений – это одна из важнейших предпосылок к последующему пониманию и трактовке полученной информации.
Число значащих цифр в промежуточном и конечном результатах определяется низшим разрядом погрешности, которая, в свою очередь не должна содержать более 2-х значащих цифр.
1. Цифры 1, 2, 3,…, 8, 9, если они приведены в записи без указания на погрешность, всегда считаются значащими;
2. Нули (“0”) в конце цифровой записи числа могут быть значимыми (такое их правило записи) и незначащими, то есть без надобности приписанными;
3. 0-и (нули) в начале числа (десятые, сотые, тысячные и другие аналоговые доли) не являются значимыми. Такого рода нули могут быть только в значении погрешности, но ни в коем случае не в результате измерений.
Примеры:
| № n/n | 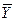 ед. измерения ед. измерения | DY ед. измерения | 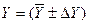 ед измерения ед измерения | |
| Промежуточный результат | Конечный результат | |||
| 1. | 71,54 | 0,322 | 74,54±0,33 | 74,5±0,4 |
| 2. | 3728,3 или 3,7283·103 | 45,2 или 0,452·102 | (3,728±0,046)·103 или (37,28±0,46)·102 | (3,73±0,05)·103 или (37,3±0,5)·102 |
| 3. | 0,37283 или 37,283·10-2 | 0,00452 или 0,46·10-2 | (37,28±0,46)·10-2 нежелательная запись: (3,728±0,046)·10-1 | (37,3±0,5)·10-2 нежелательная запись: (3,73±0,05)·10-1 |
Примечание: числа, подчеркнутые в примерах – это желательная запись.
При округлении чисел в них оставляют только верные (значащие) цифры:
Правило 1.
Округление числа до значащих цифр достигается простым отбрасыванием неверных цифр, если первая из отбрасываемых цифр меньше, чем 5. Пример: 73,42Þ73,4; 73; 0,7×102;
Правило 2.
Если первая из отбрасываемых цифр больше, чем 5, то последняя оставленная цифра увеличивается на единицу. Последняя цифра увеличивается также и в том случае, когда первая из отбрасываемых цифр – 5, а за ней есть одна или несколько цифр, отличных от нуля. Пример: различные округления числа 35,856 Þ35,86; 35,9; 36.
Правило 3.
Если отбрасываемая цифра равна 5, а за ней нет значащих цифр, то округление производит на ближайшее четное число: последняя сохраняемая цифра остается неизменной, если она четная, и увеличивается на единицу, если она нечетная. Пример: округляем до двух значащих цифр: 0,435Þ0,44; 0,465Þ0,46.
При выполнении математических операций с числами важно учитывать два обстоятельства: значащие и запасные цифры; разряды тех цифр, с которыми выполняются операции.
1. При сложении и вычитании приближенных данных измерений в окончательном результате следует сохранить столько десятичных знаков, сколько их в приближенном числе с наименьшим числом десятичных знаков:
23,2+0,442+7,247 » 23,2+0,44+7,25 = 30,89 » 30,9
2. При умножении и делении в результате следует сохранить столько значащих цифр, сколько их имеет приближенное данное с наименьшим числом значащих цифр:
30,9 × 1,8364 » 30,9 · 1,84 = 56,856 » 56,9
56,9 : 2,412 » 56,9 : 2,41 = 23,609 » 23,6
3. При возведении в степень в результате следует сохранить столько значащих цифр, сколько их имеет возводимое в степень приближенное число:
(11,38)2 = 129,5044 » 129,5
4. При извлечении корня в результате следует сохранить столько значащих цифр, сколько их имеет подкоренное число:
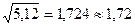
5. При нахождении логарифма приближенного числа нужно брать столько знаков, сколько верных знаков содержит данное число:
ln 77,23 » 2,8878 » 2,888
Примечание! При вычислении промежуточных результатов следует брать на одну цифру больше, чем указано в правилах округления при выполнении математических операций над числами. В окончательном результате эта “запасная” цифра отбрасывается. Приведенный ниже пример пояснит сказанное: