I. Обработка результатов прямых измерений.

При однократных прямых измерениях за погрешность, как правило, принимают цену деления измерительного инструмента. Однако, в том случае, когда ближайшие деления далеко отстоят друг от друга, за погрешность может быть принята часть деления шкалы (0,5; 0,25 цены деления). Погрешность такогооднократного измерения определяет и разряд последней значащей цифры вполученном в результате измерения числе.

С целью уменьшения случайной погрешности прямых измерений проводят их многократно и за наиболее близкое к истинному значению искомой величины принимают среднее арифметическое значение полученных “n”результатов:

(1)

Для оценки погрешности таких измерений используют:

а) среднее отклонение значения i-х величин от среднего значения (среднее отклонение от среднего). Складываются абсолютные значения отклонений (учет знаков давал бы в пределах точности измерений 0-ое значение среднего):

. (2)

б) среднеквадратичное отклонение:

. (3)

Вычисления среднеквадратичного отклонения по формуле (3) достаточно трудоемки, поэтому чаще для определения s используют приближение Питерса, связывающее среднее отклонение от среднего и среднеквадратичное отклонение s:

. (4)

Распределение Гаусса.

Среднеквадратичное отклонение характеризует вероятность попадания истинного значения величины в задаваемый интервал около 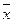. Пусть нами проведено очень большое количество измерений значения x. В итоге получено “n” результатов. Если построить график зависимости числа данных n_i от х_i, то при n→¥ получим распределение результатов называемое распределением Гаусса. Как видно из рисунка, больше всего n_i измерений будет вблизи , которое практически совпадает с истинным значением х. Чем дальше х_i отстает от , тем меньше будет таких результатов измерений.

В теории статистических измерений показано, что в интервале находятся 68% общего числа измерений, т.е. вероятность попадания в интервале ( ) 0,68. Интервалу ( ) соответствует вероятность (достоверность результата) 0,95. Правило трех сигма: ( ) - устанавливает практически 100 % вероятность попадания результата в интервал возможных значений 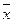(99,7 %).

Распределение Гаусса описывает случайные погрешности при бесконечно большом числе измерений. При конечном же количестве измерений для оценки вероятности попадания истинного значения характеристики в задаваемый интервал используют, так называемый, коэффициент Стьюдента (Уильяма Госета) t_{a, n} – множитель, учитывающий число измерений n и доверительную вероятность a (значения t_{n, a}. в таблице).

Таблица коэффициенов Стьюдента (коэффициентов t_n,a).

a n	10%	20%	30%	40%	50%	60%	70%	80%	90%	95%	96%	99%	99,9%
	0,16	0,33	0,51	0,73	1,00	1,38	2,0	3,1	6,3	12,7	31,8	63,7	636,3
	0,14	0,29	0,45	0,62	0,82	1,06	1,3	1,9	2,9	4,3	7,0	9,9	31,6
	0,14	0,28	0,42	0,58	0,77	0,98	1,3	1,6	2,4	3,2	4,5	5,8	12,9
	0,13	0,27	0,41	0,57	0,74	0,94	1,2	1,5	2,1	2,8	3,7	4,6	8,6
	0,13	0,27	0,41	0,56	0,73	0,92	1,2	1,5	2,0	2,6	3,4	4,0	6,9
	0,13	0,27	0,40	0,55	0,72	0,91	1,1	1,4	1,9	2,4	3,1	3,7	6,0
	0,13	0,26	0,40	0,54	0,71	0,90	1,1	1,4	1,9	2,4	3,0	3,5	5,4
	0,13	0,26	0,40	0,54	0,71	0,89	1,1	1,4	1,9	2,3	2,9	3,4	5,0
	0,13	0,26	0,40	0,54	0,70	0,88	1,1	1,4	1,8	2,3	2,8	3,3	4,8
	0,13	0,26	0,40	0,54	0,70	0,88	1,1	1,4	1,8	2,2	2,8	3,2	4,6
	0,13	0,26	0,40	0,54	0,70	0,87	1,1	1,4	1,8	2,2	2,7	3,1	4,5
	0,13	0,26	0,40	0,54	0,70	0,87	1,1	1,4	1,8	2,2	2,7	3,1	4,3
	0,13	0,26	0,39	0,54	0,70	0,87	1,1	1,4	1,8	2,2	2,7	3,0	4,2
	0,13	0,26	0,39	0,54	0,70	0,87	1,1	1,3	1,8	2,2	2,6	3,0	4,1
	0,13	0,26	0,39	0,54	0,70	0,87	1,1	1,3	1,8	2,2	2,6	2,9	4,0

Абсолютная случайная погрешность определяется как

Dx_сл= t_n,a×s. (5)

Кроме разброса значений, в полученных данных, каждое измерение выполняется с погрешностью прибора Dx_пр, равном цене (или доле цены деления) прибора. Величину, учитывающую и это обстоятельство, называют абсолютной погрешностью многократных измерений - Dx:

. (6)

Результат измерений записывается в виде:

. (7)

Эта запись означает, что истинное значение физической величины x находится в указанном интервале с вероятностью a.

Относительная погрешность – это величина, показывающая «качество» измерений. Она равна:

.

Результаты прямых измерений (их желательно провести не менее пяти раз) и обработку полученных данных рекомендуем представить в таблицах:

Таблица 1.

			…	n	средние значения
хi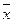
Dхi=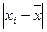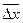
Приборная погрешность	Dхпр

Вычисления:

Таблица 2.

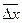		s	ta,n	Dхсл	Dхпр	Абсолютная погрешность	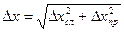Относительная погрешность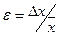
промежут.
конечная

Итоговые данные прямых измерений могут быть представлены, как промежуточный, так и конечный результаты:

- результат принято считать промежуточным, если он будет использован в последующем для расчетов косвенно определяемой физической характеристики;

- в промежуточных данных желательно иметь одну запасную цифру. Разряд запасной цифры должен быть на один разряд ниже величин прямых измерений;

- промежуточный результат в абсолютной погрешности, как правило, содержит две цифры.

Нижний разряд погрешности и среднего значения результата измерений должны совпадать. Округление погрешности всегда проводится в сторону завышения, а результата измерений – по общим правилам (см. раздел II).

- практически общепринятой формой записи окончательного результата измерений принята следующая: а) в абсолютной погрешности сохраняется две значащих цифры, если первая из них 1 или 2, б) начиная с цифры 3, в погрешности сохраняется только одна значащая цифра.

Запись промежуточного и конечного результатов желательно сделать в рациональной форме, т.е. числом с единицами, десятыми и сотыми и другими долями и общим множителем.

10ⁿ. “n” – конечное целое число, но не желательно, чтоб оно принимало значения ±1.

Примеры:

1. (0,04528 ± 0,00073)_{ед. изм.} Þ промежуточный результат = (4,528 ± 0,073)·10^-2_{ед. изм.} Þ конечный результат = (4,53 ± 0,08)·10^-2 ед. изм.

2. Промежуточный результат; конечный результат

(45,22 ± 0,31) _{ед. изм.} = (45,2 ± 0,4)_{ед. изм.}