Закон Сохранения Механической Энергии

Закон Сохранения Механической Энергии

Если в замкнутой системе не действуют силы, трения и силы сопротивления, то сумма кинетической и потенциальной энергии всех тел системы остается величиной постоянной.

Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только посредством сил тяготения и упругости, то работа этих сил равна изменениюпотенциальной энергиител, взятому с противоположным знаком:

A= –(Eр2–Eр1).

По теореме о кинетической энергии эта работа равна изменению кинетической энергии тел (см. §1.19):

Следовательно

или

Ek1+Ep1=Ek2+Ep2.

Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой посредством сил тяготения и сил упругости, остается неизменной.

Это утверждение выражает закон сохранения энергии в механических процессах. Он является следствием законов Ньютона. Сумму E=E_k+E_p называют полной механической энергией. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии.

ДИССИПАЦИЯ ЭНЕРГИИ

лат. рассеяние) — переход части энергии упорядоченных процессов (кинетической энергии движущегося тела, энергии электрического тока и т. п.) в энергию неупорядоченных процессов, в конечном счете — в теплоту (см. Диссипация, Системы диссипативные). Если диссипация энергии происходит в замкнутой системе, то энтропия системы возрастает (см. Энтропия). Диссипация энергии в открытых системах, обусловленная процессами уноса энергии из системы, например в виде излучения, может приводить к уменьшению энтропии рассматриваемой системы при увеличении полной энтропии системы и окружающей среды. (См. Теория горячей вселенной).

22. Удар (или соударение)- это столкновение двух или более тел, при котором взаимодействие длится очень короткое время. Исходя из данного определения, кроме явлений, которые можно отнести к уда­рам в прямом смысле этого слова (столкновение атомов или биллиард­ных шаров), сюда можно отнести и такие, как удар человека о землю при прыжке с трамвая и др. При ударе в телах возникают столь зна­чительные внутренние силы, что внешними силами, действующими на них, можно пренебречь. Это позволяет рассматривать соударяющиеся тела как замкнутую систему и применять к ней законы сохранения.

Тела во время удара претерпевают деформацию. Сущность удара заключается в том, что кинетическая энергия относительного движе­ния соударяющихся тел на короткое время преобразуется в энергию упругой деформации. Во время удара имеет место перераспределение энергии между соударяющимися телами. Наблюдения показывают, что относительная скорость тел после удара не достигает своего прежнего значения. Это объясняется тем, что нет идеально гладких поверхностей. Отношение нормальных составляющих относительной скорости тел после и до удара называется коэффициентом восстановления e:

Если для сталкивающихся тел e=0, то такие тела называются абсолютно неупругими, если e=1 – абсолютно упругими. На практике для всех тел 0<e<1 ( например, для стальных шаров e»0.56, для шаров из слоновой кости e»0.89, для свинца e»0). Однако в некоторых случаях тела можно с большой точностью рассматривать либо как абсолютно упругие, либо как абсолютно неупругие.

Прямая, проходящая через точку соприкосновения тел и нормаль­ная к поверхности их соприкосновения, называется линией удара. Удар называется центральным, если тела до удара движут­ся вдоль прямой, проходящей через их центры масс. Мы будем рас­сматривать только центральные абсолютно упругие и абсолютно неуп­ругие удары.

Абсолютно упругий удар - столкновение двух тел, в результате которого в обоих взаимодействующих телах не остается никаких деформаций и вся кинетическая энергия, которой обладали тела до удара, после удара снова превращается в кинетическую энер­гию. Для абсолютно упругого удара выполняются закон сохранения им­пульса и закон сохранения кинетической энергии.

Обозначим скорости шаров массами m₁ и m₂ до удара через и , после удара - через и (рис. 15).

Рис. 15

При прямом центральном ударе векторы скоростей шаров до и после удара лежат на прямой линии, соединяющей их центры. Проекции векторов скорости на эту линию равны модулям скоростей.

Их направления учтем знаками: положительное значение припи­шем движению вправо, отрицательное - движению влево.

При указанных допущениях законы сохранения имеют вид

(3.14)

. (3.15)

Произведя соответствующие преобразования в выражениях (3.14) и (3.15), получим

(3.16)

(3.17)

откуда (3.18)

Решая уравнения (3.16) и (3.18), находим

, (3.19)

. (3.20)

Разберем несколько примеров.

1. При v₂ = О

, (3.21)

. (3.22)

23. Вращательное движение – это движение твердого тела, имеющего как минимум две неподвижные точки (рисунок 1.3). Прямая, проходящая через эти точки, называется осью вращения. Положение тела определено, если задан угол φ между плоскостями П₀ и П , одна из которых неподвижна, а другая жестко связана с телом.

φ=φ(t) – уравнение вращательного движения твердого тела.

За положительное направление отсчета принимается вращение против хода часовой стрелки, если смотреть навстречу положительному направлению оси z. Траекториями точек тела при его вращении вокруг неподвижной оси являются окружности, расположенные в плоскостях, перпендикулярных оси вращения.

Для характеристики изменения угла поворота с течением времени вводится величина, называемая угловой скоростью ω:

В технике угловая скорость – это частота вращения, выраженная в оборотах в минуту. За одну минуту тело повернется на угол 2π⋅ n, где n – число оборотов в минуту (об/мин). Разделив этот угол на число секунд в минуте, получим

Вектор угловой скорости – это вектор, направленный по оси вращения в ту сторону, откуда вращение видно происходящим против хода часовой стрелки, с модулем, равным модулю алгебраической угловой скорости

где k – единичный вектор оси вращения.

Угловое ускорение – мера изменения угловой скорости:

Вектор углового ускорения – производная вектора угловой скорости по времени

сли угловое ускорение ε=const, то вращательное движение называется равнопеременным.

Уравнение равнопеременного вращения

и уравнение, выражающее угловую скорость в любой момент времени

ω=ω₀+εt

24. УРАВНЕНИЕ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ

Твердое тело как система материальных точек. Движение центра инерции твердого тела. Кинетическая энергия вращающегося тела. Понятие момента инерции относительно неподвижной оси. Теорема Штейнера. Моменты инерции некоторых простейших тел. Уравнение динамики вращательного движения относительно неподвижной оси.

Движение твердого тела в общем случае определяется двумя векторными уравнениями. Одно из них - уравнение движения центра масс (4.11), другое-уравнение моментов вС-системе (6.24):

(10.1)

Зная законы действующих внешних сил, точки их приложения и начальные условия, можно с помощью этих уравнений найти как скорость, так и положение каждой точки твердого тела в любой момент времени, т. е. полностью решить задачу о движении тела. Однако, несмотря на кажущуюся простоту уравнений (10.1), решение их в общем случае представляет собой весьма трудную задачу. Это прежде всего обусловлено тем обстоятельством, что связь между собственным моментом импульса и скоростями отдельных точек твердого тела в С-системе оказывается сложной, за исключением немногих частных случаев. Мы не будем рассматривать эту задачу в общем виде (она решается в курсе теоретической механики) и ограничимся в дальнейшем только отдельными частными случаями.

Формула Торричелли

Закон Торричелли показывает, что при истечении идеальной нестискувальнои жидкости из щели в боковой стенке или на дне сосуда жидкость приобретает скорость тела, падающего с определенной высоты. С помощью этого можно вычислить максимальный уровень утечки жидкости из сосуда. Для подтверждения можно воспользоваться законом Бернулли, выведя из него формулу Торричелли: ρgh + p ₀ = (pV ²⁾ / 2 + p _0, где p0 - атмосферное давление, h - высота столба жидкости в сосуде, V - скорость истечения жидкости. Отсюда V = √ 2gh.

31. Вязкость (внутреннее трение) —это свойство реальных жидкостей оказывать сопротивление перемещению одной части жидкости относительно другой. При перемещении одних слоев реальной жидкости относительно других возникают силы внутреннего трения, направленные по касательной к поверхности слоев. Действие этих сил проявляется в том, что со стороны слоя, движущегося быстрее, на слой, движущийся медленнее, действует ускоряющая сила. Со стороны же слоя, движущегося медленнее, на слой, движущийся быстрее, действует тормозящая сила.

Сила внутреннего трения F тем больше, чем больше рассматриваемая площадь поверхности слоя S (рис. 52), и зависит от того, насколько быстро меняется скорость течения жидкости при переходе от слоя к слою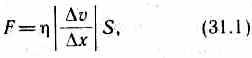

36. -----------------------------------

37. Термодинамическое равновесие

Утверждается, что любая замкнутая термодинамическая система, для которой внешние условия остаются неизменными, с течением времени переходит в равновесное состояние, в котором прекращаются все макроскопические процессы. Внешние параметры – это величины, определяемые положением не входящих в систему тел - (объем, магнитная индукция, напряженность электрического поля)

Внешние параметры являются функциями координат внешних тел.

Внутренние параметры – это величины, определяемые совокупным

движением и распределением в пространстве входящих в систему частиц

(температура, давление, внутренняя энергия, плотность, поляризованность,

намагниченность)

Закон Сохранения Механической Энергии

Если в замкнутой системе не действуют силы, трения и силы сопротивления, то сумма кинетической и потенциальной энергии всех тел системы остается величиной постоянной.

Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только посредством сил тяготения и упругости, то работа этих сил равна изменениюпотенциальной энергиител, взятому с противоположным знаком:

A= –(Eр2–Eр1).

По теореме о кинетической энергии эта работа равна изменению кинетической энергии тел (см. §1.19):

Следовательно

или

Ek1+Ep1=Ek2+Ep2.