Распределение электронов в атоме по состояниям

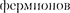Если частицы имеют одинаковые квантовые числа, то их вол- новая функция симметрична относи- тельно перестановки частиц. Отсюда следует, что два одинаковых фермиона, входящих в одну систему, не могут на- ходиться в одинаковых состояниях, так как для волновая функция должна быть антисимметричной. Обоб- щая опытные данные, В. Паули сформу- лировал принцип, согласно которому системы фермионов встречаются в природетолько состояниях, описыва- емых антисимметричными волновыми функциями 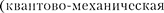формулировка принципа Паули).

Из этого положения вытекает более простая формулировка принципа Пау- ли, которая и была введена им в кван- товую теорию (1925) еще до утвержде- ния квантовой механики: в системе оди- наковых 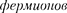любые два из нихне могутодновременнонаходиться одном томжесостоянии. Отметим, что чис- ло однотипных бозонов, находящихся в одном и том же состоянии, лими-

тируется.

Напомним, что состояние электро- на в атоме однозначно определяется набором четырех квантовых чисел:

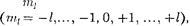главного п 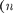= 1, 2, 3,...), орбитального 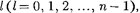магнитного

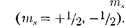магнитного спинового

Распределение электронов в атоме подчиняется принципу Паули, кото- рый может быть использован в его про- стейшей формулировке: в одном и том атоме неможет быть более одного

Главное квантовое число п

Символ оболочки

К

L

м

N

О

Максимальное число электронов в оболочке

Орбитальное квантовое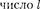

Символ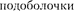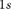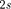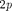

3 s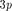

3d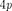

Ad

4/

5s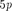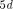

5/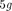

Максимальное число электронов в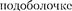

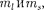электронасодинаковымнаборомчеты- рех квантовых чисел п, 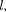т.е.

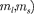
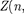/, = 0 или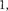

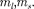где 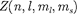— число электронов, находящихся в квантовом состоянии, описываемом набором четырех кванто- вых чисел: п, /,

Таким образом, принцип Паули ут- верждает, что два электрона, связанные в одном и том же атоме, различаются значениями по крайней мере одного квантового числа.

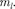
Согласно формуле (223.8), данному п соответствует п2различных состояний, отличающихся значениями / и Кван- товое число может принимать лишь два значения Поэтому макси- мальное число электронов, находящих- ся в состояниях, определяемых данным главным квантовым числом, равно

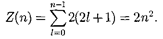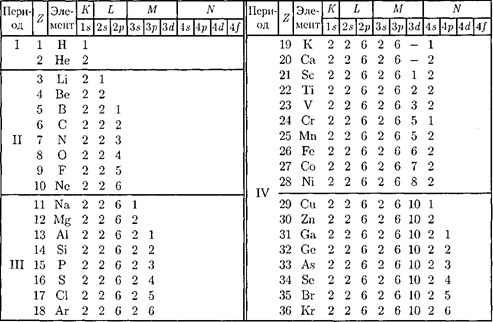
Совокупность электронов в электронном атоме, имеющих одно и то же главное квантовое число п, называ- ют электронной оболочкой. В каждой из оболочек электроны распределяют- ся по соответствующим данному Поскольку орбитальное квантовое число принимает значения

от 0 до п — 1, число 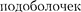равно порядковому номеру п оболочки. Коли- чество электронов в гюдоболочке опре- деляется магнитным и магнитным спи- новым квантовыми числами: макси- мальное число электронов в подоболоч- ке с данным /равно 2(2/ + 1). Обозна- чения оболочек, а также распределение электронов по оболочкам и подоболоч- кам в табл.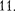

§ 228. Периодическая система элементов Менделеева

Принцип Паули лежит в основе си- стематики заполнения электронных со- стояний в атомах и позволяет объяс- нить Периодическую систему эле- ментов Д.И.Менделеева (1869) — фундаментальный закон природы, яв- ляющийся основой современной хи- мии, атомной и ядерной физики.

Д.И.Менделеев ввел понятие по- рядкового номера Z химического эле- мента, равного числу протонов в ядре и соответственно равного общему числу электронов в электронной оболочке атома. Расположив химические элемен- ты по мере возрастания порядковых но- меров, он получил периодичность в из- менении химических свойств элемен- тов. Однако для известных в то время

64 химических элементов некоторые клетки таблицы оказались незаполнен- ными, так как соответствующие им эле- менты (например, Ga, Se, Ge) тогда еще не были известны. Д. Менделеев, та- ким образом, не только правильно рас- положил известные элементы, но и предсказал существование новых, еще не открытых элементов и их основные свойства. Кроме того, ему удалось уточ- нить атомные веса некоторых элемен- тов. Например, атомные веса и U, вычисленные на основе таблицы Мен- делеева, оказались правильными, а по- лученные ранее экспериментально — ошибочными.

Так как химические и некоторые физические свойства элементов опреде- ляются внешними (валентными) элек- тронами в атомах, то периодичность свойств химических элементов должна быть связана с определенной периодич- ностью в расположении электронов в

атомах. Поэтому для объяснения табли- цы будем считать, что каждый последу- ющий элемент образован из предыду- щего 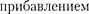к ядру одного про- тона и соответственно прибавлением одного электрона в электронной обо- лочке атома. Взаимодействием электро- нов пренебрегаем, внося, где это необ- ходимо, соответствующие поправки. Рассмотрим атомы химических элемен- тов, находящиеся в основном состоя- нии.

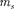Единственный электрон атома водо- рода находится в состоянии 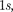харак- теризуемом квантовыми числами п — 1, 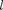= 0, — О и — 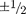(ориентация его спина произвольна). Оба электро- на атома Не находятся в состоянии 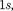но с антипараллелыюй ориентацией спина. Электронная конфигурация для атома Не записывается как 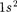(два

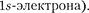На атоме Не заканчива-

ется заполнение 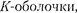что соот-

12

ветствует завершению I периода Пери- одической системы элементов Менде- леева (табл. 12).

Третий электрон атома Li (Z= 3), со- гласно принципу Паули, уже не может разместиться в целиком заполненной

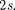
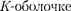и занимает наинизшее энер- гетическое состояние с в = 2 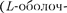ка), т. е. 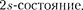Электронная кон- фигурация для атома Li: 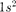2 s. Атомом Li начинается II период Периодической системы элементов. Четвертым элект- роном Be (Z = 4) заканчивается запол- нение подоболочки У следующих шести элементов от В (Z = 5) до Ne

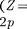
10) идет заполнение подоболочки (табл. 12). II период Периодической системы заканчивается — инер- тным газом, для которого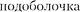

2р целиком заполнена.

Одиннадцатый электрон Na (Z= 11) размещается в М-оболочке (п = 3), за- нимая наинизшее состояние 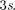Элект- ронная конфигурация имеет вид

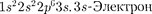
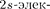(каки

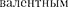
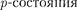трон Li) является электро- ном, поэтому оптические свойства Na подобны свойствам Li. С Z = 12 идет последовательное заполнение М-обо- лочки. А 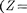18) оказывается подоб- ным Не и Ne: в его наружной оболочке все s- и заполнены. 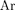яв- ляется химически инертным и завер- шает III период Периодической сис- темы.

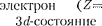
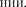Девятнадцатый К 19) должен был бы занять в М- оболочке. Однако и в оптическом, и в химическом отношениях атом К схож с атомами Li и Na, которые имеют вне- шний 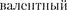электрон в s-состоя- Поэтому 19-й валентный электрон

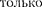К должен также находиться в s-состоя- нии, но это может быть s-состоя- ние новой оболочки (TV-оболочки), т. е. заполнение TV-оболочки для К начина-

ется при незаполненной М-оболочке. Это означает, что в результате взаимо- действия электронов состояние п = 4,

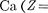/ = 0 имеет меньшую энергию, чем со- стояние п = 3, 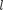2. Спектроскопичес- кие и химические свойства 20) показывают, что его 20-й электрон также находится в 45-состоянии TV-оболочки.

В последующих элементах происхо- дит заполнение М-оболочки [от Sc

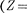
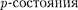21) до Zn (Z= 30)]. Далее TV-обо- лочка заполняется до 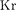(Z = 36), у которого опять-таки, как и в случае Ne и 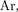s- и наружной обо- лочки заполнены целиком. Криптоном заканчивается IV период Периодиче- ской системы. Подобные рассуждения применимы и к остальным элементам таблицы Менделеева, однако эти дан- ные можно найти в справочниках. От- метим лишь, что и начальные элемен- ты последующих периодов Rb, Cs, Fr яв- ляются щелочными металлами, а их последний электрон находится в s-co-

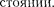
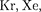
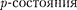Кроме того, атомы инертных газов 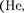Ne, 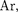Rn) занимают в таблице особое положение — в каж- дом из них 5- и наружной оболочки целиком заполнены и ими за- вершаются очередные периоды Перио- дической системы.

Каждую из двух групп элементов — лантаниды [от лантана 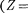57) до лю- теция (Z = 71)] и актиниды [от акти- ния (Z= 89) до лоуренсия 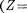103)] — приходится помещать в одну клетку таблицы, так как химические свойства элементов в пределах этих групп очень близки. Это объясняется тем, что для лантанидов заполнение подоболочки 4/, которая может содержать 14 электро- нов, начинается лишь после того, как целиком заполнятся подоболочки 5s, Ър 6 s. Поэтому для этих элементов вне- шняя Р-оболочка (6s2) оказывается одинаковой. Аналогично, одинаковой

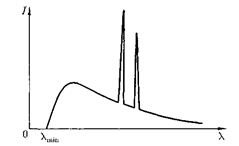для актинидов является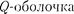

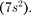
Таким образом, открытая Менделе- евым периодичность в химических свойствах элементов 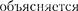по- вторяемостью в структуре внешних оболочек у атомов родственных эле- ментов. Так, инертные газы имеют оди- наковые внешние оболочки из 8 элект- ронов (заполненные s- 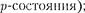во внешней оболочке щелочных метал- лов (Li, Na, К, Rb, Cs, Fr) имеется лишь один 5-электрои; во внешней 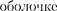щелочно-земельных металлов (Be, Mg,

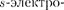
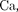Sr, 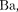Ra) имеется два

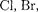
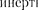на; галоиды (F, I, At) имеют вне- шние оболочки, в которых недостает одного электрона до оболочки ю- го газа, и т.д.

§229.Рентгеновскиеспектры

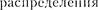Большую роль в выяснении строе- ния атома, а именно

электронов по оболочкам, сыграло из- лучение, открытое в 1895 г. немецким физиком В. Рентгеном (1845 — 1923) и названное рентгеновским.

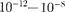Самым распространенным источни- ком рентгеновского излучения являет- ся рентгеновская трубка, в которой сильно ускоренные электрическим по- лем электроны бомбардируют анод (ме- таллическая мишень из тяжелых метал- лов, например W или Pt), испытывая на нем резкое торможение. При этом возникает рентгеновское излучение, представляющее собой электромагнит- ное излучение с длиной волны пример- но м. Волновая природа рен- тгеновского излучения доказана опыта- ми по его дифракции (см. §

Исследование спектрального соста- ва рентгеновского излучения показыва- ет, что его спектр имеет сложную струк-

309

туру (рис. 309) и зависит как от энер- гии электронов, так и от материала ано- да. Спектр представляет собой наложе- ние сплошного спектра, ограниченного со стороны коротких длин волн неко- торой границей 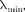называемой гра- ницей сплошного спектра, линейча- того спектра — совокупности отдель- ных линий, появляющихся на фоне сплошного спектра.

Исследования показали, что харак- тер сплошного спектра не зависит от материала анода, а определяется толь- ко 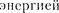бомбардирующих анод электронов. Детальное исследование свойств этого излучения показало, что оно испускается бомбардирующими анод электронами в результате их тор- можения при взаимодействии с атома- ми мишени. Сплошной рентгеновский спектр поэтому называют тормозным спектром. Этот вывод находится в со- с классической теорией излуче-

ния, так как при торможении движу- щихся зарядов должно действительно возникать излучение со сплошным спектром.

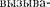Из классической теории, однако, не вытекает существование коротковол- новой границы сплошного спектра. Из опытов следует, что чем больше кине- тическая энергия электронов,

ющих тормозное рентгеновское излуче- ние, тем меньше 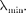Это обстоятель- ство, а также наличие самой границы

объясняются квантовой теорией. Оче- видно, что предельная энергия кванта соответствует такому случаю торможе- ния, при котором вся кинетическая энергия электрона переходит в энергию кванта, т. е.

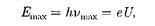
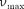где —частота, соответствующая границе сплошного спектра; U —раз- ность потенциалов, засчет которой электрону сообщается энергия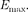

Отсюда граничная длина волны

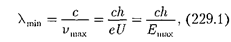
что полностью соответствует экспери- ментальным данным. Измеряя границу рентгеновского сплошного спектра, по формуле (229.1) можно определить эк- спериментальное значение постоянной Планка h, которое наиболее точно со- впадает с современными данными.

При достаточно большой энергии бомбардирующих анод электронов на фоне сплошного спектра появляются отдельные резкие линии — линейчатый спектр, определяемый материалом ано- да и называемый характеристичес- ким рентгеновским (излу- чением).

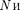
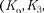По сравнению с оптическими спек- трами характеристические рентгено- вские спектры элементов совершенно однотипны и состоят из нескольких се- рий, обозначаемых К, L, M, О. Каж- дая серия, в свою очередь, содержит небольшой набор отдельных линий, обозначаемых в порядке убывания дли- ны волны индексами а, (3, ...

..., ...).

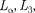
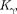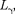При переходе от легких элементов к тяжелым структура характеристическо- го спектра не изменяется, лишь весь спектр смещается в сторону коротких волн. Особенность этих спектров зак-

лючается в том, что атомы каждого хи- мического элемента, независимо от того, ли они в свободном стоянии или входят в химическое со- единение, обладают определенным, присущим только данному элементу линейчатым спектром характеристи- ческого излучения. Так, если анод со- стоит из нескольких элементов, то и ха- рактеристическое рентгеновское излу- чение представляет собой наложение спектров этих элементов.

Рассмотрение структуры и особен- ностей характеристических рентгено- вских спектров приводит к выводу, что их возникновение связано с процесса- ми, происходящими во внутренних, за- строенных электронных оболочках атомов, которые имеют сходное строе- ние.

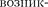Разберем механизм возникновения рентгеновских серий, который схемати- чески показан на рис. 310. Предполо- жим, что под влиянием внешнего элек- трона или высокоэнергетического фо- тона вырывается один из двух электро- нов атома. Тогда на его ме- сто может перейти электрон с более уда- ленных от ядра оболочек L,M,N,... . Та- кие переходы сопровождаются испуска- нием рентгеновских квантов и

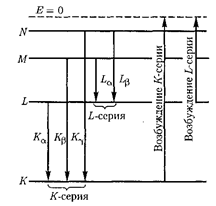Рис.310

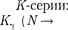новениемспектральныхлиний

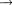
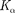(L К), 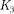(М К), К)

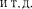
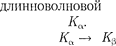Самой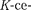

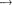рии является линия Частоты линий возрастают в ряду 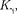по- скольку энергия, высвобождаемая при переходе электрона на 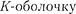с более удаленных оболочек, увеличива- ется.

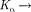
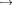Наоборот, интенсивности линий в ряду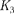 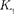убывают, так как вероятность переходов электронов с

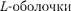на 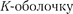больше, чем с более удаленных оболочек М и N. 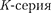сопровождается обязательно другими сериями, так как при испуска- нии ее линий появляются вакансии в оболочках L, М, ..., которые будут за- полняться электронами, находящими- ся на более высоких уровнях.

Аналогично возникают и другие се- рии, наблюдаемые, впрочем, только для тяжелых элементов. Рассмотренные линии характеристического излучения могут иметь тонкую структуру, по- скольку уровни, определяемые глав- ным квантовым числом, расщепляют- ся согласно значениям орбитального и магнитного квантовых чисел.

Исследуя рентгеновские спектры элементов, английскийфизик Г. Мозли (1887-1915) установил в 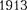г. соот- ношение, называемое законом Мозли:

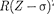= 1(229.2)

где v — частота, соответствующая дан- ной линии характеристического рент- геновского излучения; R — постоянная Ридберга; — постоянная экранирова- ния; т = 1, 2, 3,...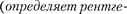

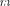новскую серию), п принимает целочис- ленные значения, начиная с + 1 (оп- ределяет отдельную линию соответ- ствующей серии).

Закон Мозли (229.2) подобен обоб- щенной формуле Бальмера (209.3) для атома водорода.

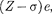Смысл постоянной экранирования заключается в том, что на электрон, со- вершающий переход, соответствующий некоторой линии, действует не весь за- ряд ядра 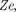а заряд ослаблен- ный экранирующим действием других электронов. Например, для 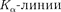а = 1, и закон Мозли запишется в виде

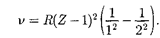
§ 230. Молекулы: химические связи, понятие об энергетических уровнях

Молекула — наименьшая частица вещества, состоящая из одинаковых или различных атомов, соединенных между собой химическими связями, и являющаяся носителем его основных химических и физических свойств. Хи- мические связи обусловлены взаимо- действием внешних, валентных элект- ронов атомов. Наиболее часто в моле- кулах встречается два типа связи: ион- ная (см. § 71).

Ионная связь (например, в молеку- лах 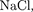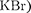осуществляется элект- ростатическим взаимодействием ато- мов при переходе электрона одного атома к другому, т.е. при образовании положительного и отрицательного

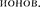
Ковалентная связь (например, в молекулах 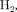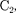СО) осуществляется при обобществлении валентных элект- ронов двумя соседними атомами (спи- ны валентных электронов должны быть антипараллельны).

Ковалентная связь объясняется на основе принципа неразличимости тож-

Явственных частиц (см. § 226), напри- мер электронов в молекуле водорода. Неразличимость частиц приводит к специфическому взаимодействию меж- ду ними, называемому обменным вза- имодействием. Это чисто квантовый эффект, не имеющий классического объяснения, его можно себе предста- вить так, что электрон каждого из ато- мов молекулы водорода проводит неко- торое время у ядра другого атома и, сле- довательно, осуществляется связь обо- их атомов, образующих молекулу. При сближении двух водородных атомов до расстояний порядка боровского радиу- са возникает их взаимное притяжение и образуется устойчивая молекула во- дорода.

Молекула является квантовой сис- темой; она описывается уравнением Шредингера, учитывающим движение электронов в молекуле, колебания ато- мов молекулы, вращение молекулы. Решение этого уравнения — очень слож- ная задача, которая обычно разбивает- ся на две: для электронов и ядер.

Энергия изолированной молекулы

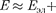
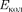
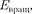(230.1)

где 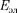— энергия движения электронов относительно ядер; 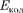— энергия ко- лебаний ядер (в результате которых периодически изменяется относитель- ное положение ядер); 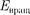— энергия вращения ядер (в результате которых периодически изменяется ориентация молекулы в пространстве).

В формуле (230.1) не учтены энер- гия поступательного движения центра масс молекулы и энергия ядер атомов в молекуле. Первая из них не квантует- ся, поэтому ее изменения не могут при- вести к возникновению молекулярно- го спектра, а вторую можно не учиты- вать, если рассматривать сверхтон- кую структуру спектральных линий.

Отношения =

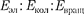
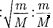
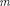где — масса электрона; М— величина, имеющая порядок массы ядер атомов

в молекуле, — 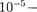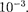Поэтому

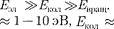
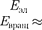
Доказано, что

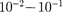эВ,

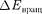Каждая из входящих в выражение (230.1) энергий квантуется (ей соответ- ствует набор дискретных уровней энер- гии) и определяется квантовыми чис- лами. При переходе из одного энерге- тического состояния в другое поглоща- ется или испускается энергия 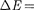hv. При таких переходах одновременно из- меняются энергия движения электро- нов,энергии колебанийи вращенияядер. Из теории и эксперимента следует, что расстояние между вращательными уровнями энергии гораздо мень-

Электронные уровни

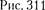432

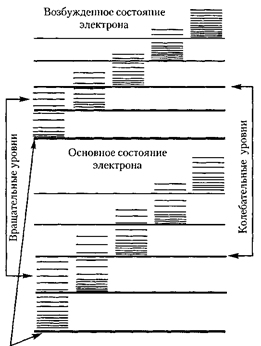
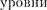ше расстояния между колебательными уровнями 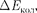которое, в свою оче- редь, меньше расстояния между элект- ронными уровнями 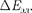На рис. схематически представлены

энергии двухатомной молекулы (для примера рассмотрены только два элек- тронных уровня — показаны жирными

Как будет показано в § 231, структу- ра энергетических уровней молекул определяет их спектр излучения, возни- кающий при квантовых переходах меж- ду соответствующими энергетическими уровнями.

§ 231. Молекулярные спектры. Комбинационное рассеяние света

Строение молекул и свойства их энергетических уровней проявляются в молекулярных спектрах — спектрах излучения (поглощения), возникаю- щих при квантовых переходах между уровнями энергии молекул. Спектр из- лучения определяется струк- турой ее энергетических уровней и со- ответствующими правилами отбора (например, изменение квантовых чи- сел, соответствующих как колебатель- ному, так и вращательному движению, должно быть равно ±1).

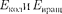Итак, при разных типах переходов между уровнями возникают различные типы молекулярных спектров. Частоты спектральных линий, испускаемых мо- лекулами, могут соответствовать пере- ходам с одного электронного уровня на другой (электронные спектры) или с одного колебательного (вращательно- го) уровня на другой [колебательные (вращательные) спектры]. Кроме того, возможны и переходы с одними значениями пауровни, име- ющие другие значения всех трех ком-

понентов, в результате чего возникают электронно-колебательные ко- лебательно-вращательные спек- тры. Поэтому спектр молекул доволь- но

Типичные молекулярные спект- ры — полосатые, представляют собой совокупность более или менее узких по- лос в ультрафиолетовой, видимой и ин- фракрасной областях. Применяя спек- тральные приборы высокой разрешаю- щей способности, можно видеть, что полосы представляют собой настолько тесно расположенные линии, что они с трудом разрешаются.

Структура молекулярных спектров различна для разных молекул и с уве- личением числа атомов в молекуле ус- ложняется (наблюдаются лишь сплош- ные широкие полосы). Колебательны- ми и вращательными спектрами обла- дают только многоатомные молекулы, а двухатомные их не имеют. Это объяс- няется тем, что двухатомные молекулы не имеют дипольиых моментов (при ко- лебательных и вращательных перехо- дах отсутствует изменение диполыюго момента, что является необходимым условием отличия от нуля вероятнос- ти перехода).

В 1928 г. академики Г. (1890-1957) и Л.И.Мандельштам, а также индийские физики

(р. 1911) од-

новременно открыли явление комби- национного рассеяния света. Если на вещество (газ, жидкость, прозрачный кристалл) падает строго монохромати- ческий свет, то в спектре рассеянного света помимо несмещенной спектраль- ной линии обнаруживаются новые ли- нии, частоты которых представляют собой суммы или разности частоты v падающего света и частот собствен- ных колебаний (или вращений) моле- кул рассеивающей среды.

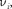
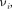Линии в спектре комбинационного рассеяния с частотами у — меньши- ми частоты v падающего света, называ- ются стоксовыми (или красными) спутниками, линии с частотами v + большими v, — антистоксовыми(или фиолетовыми) спутниками.

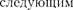
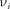
Анализ спектров комбинационного рассеяния приводит к вы- водам: 1) линии спутников располага- ются симметрично по обе стороны от несмещенной линии; 2) частоты не за- висят от частоты падающего на веще- ство света, а определяются только рас- сеивающим веществом, т.е. характери- зуют его состав структуру; 3) число спутников определяется рассеивающим веществом; 4) интенсивность антисток- совых спутников меньше интенсивно- сти стоксовых и с повышением темпе- ратуры рассеивающего вещества увели- чивается, в то время как интенсивность стоксовых спутников практически от температуры не зависит.

Объяснение закономерностей ком- бинационного рассеяния света дает квантовая теория. Согласно этой тео- рии, рассеяние света есть процесс, в ко- тором один фотон поглощается и один фотон испускается молекулой. Если энергии фотонов одинаковы, то в рас- сеянном свете наблюдается несмещен- ная линия. Однако возможны процес- сы рассеяния, при которых энергии по- глощенного и испущенного фотонов неодинаковы. Различие энергии фото- нов связано с переходом молекулы из нормального состояния в возбужденное (испущенный фотон будет иметь мень- шую частоту — возникает стоксов спут- ник), либо из возбужденного

в нормальное (испущенный фотон бу- дет иметь большую частоту — возника- ет антистоксов спутник).

Рассеяние света сопровождается пе- реходами молекулы между различны-

ми колебательными или вращательны- ми уровнями, в результате чего и воз- никает ряд симметрично расположен- ных спутников. Число спутников, та- ким образом, определяется энергети- ческим спектром молекул, т. е. зависит только от природы рассеивающего ве- щества. Так как число возбужденных молекул гораздо меньше, чем число не- возбужденных, то интенсивность анти- стоксовых спутников меньше, чем сто- ксовых. С повышением температуры число возбужденных молекул растет, в результате чего возрастает и интенсив- ность антистоксовых спутников.

Молекулярные спектры (в том чис- ле и спектры комбинационного рассея- ния света) применяются для исследо- вания строения и свойств молекул, ис- пользуются в молекулярном спектраль- ном анализе, лазерной спектроскопии, квантовой электронике и т. д.

§ 232. Поглощение. Спонтанное и вынужденное излучения

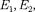
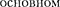
Как отмечалось выше, атомы могут находиться лишь в квантовых состоя- ниях с дискретными значениями энер- гии 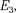... . Ради простоты рас- смотрим только два из этих состояний 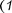и 2) с энергиям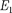и и 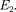Если атом находится в 1,

под действием внешнего излучения может осуществиться вынужденный переход в возбужденное состояние 2 (рис. 312, а), приводящий к поглоще- нию излучения. Вероятность подобных переходов пропорциональна плотности излучения, вызывающего