Уравнение Шредингера для стационарных состояний

Из статистического толкования волн де Бройля (см. § 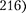и соотношения не- определенностей Гейзенберга (см. § 215) следовало, что уравнением движения в квантовой механике, описывающим движение микрочастиц в различных силовых полях, должно быть уравне- ние, из которого бы вытекали наблю- даемые на опыте волновые свойства частиц.

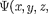
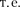
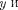Основное уравнение должно быть уравнением относительно волновой функции 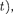так как именно она, или, точнее, величина |Ф|2, определяет вероятность пребывания частицы в мо- мент времени t в объеме dV, в обла- сти с координатами и х + dx, y+dy,

z и 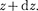Так как искомое уравнениедолжно учитывать волновые свойства частиц, то оно должно быть волновым уравнением, подобно уравнению, опи- сывающему электромагнитные волны. Основное уравнение нерелятивист- ской квантовоймеханики сформулиро- вано в 1926 г. Э.Шредингером. Урав- нение Шредингера, как и все основные уравнения физики (например, уравне- ния Ньютона в классической механике и уравнения Максвелла для электро- магнитного поля), не выводится, а по- стулируется. Правильность этого урав- нения подтверждается согласием с опы- том получаемых с его помощью резуль- татов, что, в свою очередь, придает ему характер закона природы. Уравнение

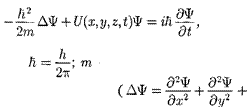Шредингера имеет вид

(217.1)

д е —

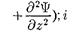г масса частицы; А — оператор Лапласа

— мнимаяединица, 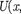y,z,t) —

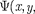потенциальная функция частицы в си- ловом поле, в котором она движется; z,t) — искомая волновая функция

частицы.

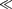Уравнение 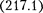справедливо для любой частицы (со спином, равным 0; см. § 225), движущейся с малой (по сравнению со скоростью света) скоро- стью, т. е. со скоростью v с. Оно до- полняется условиями, накладываемы- ми на волновую функцию: 1) волновая функция должна быть конечной, одно- значной и непрерывной (см. § 216);

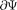
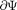
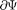
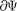
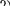
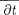
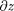2) производные —, —, —-, долж-

дх ду

ны быть непрерывны; 3) функция |Ф|2 должна быть интегрируема; это усло- вие в простейших случаях сводится к

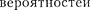условию нормировки (216.3).

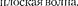
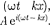Чтобы прийти к уравнению Шредингера, рассмотрим свободно движущуюся частицу, которой, согласно де Бройля, сопостав- ляется Для простоты рассмот- рим одномерный случай. Уравнение плоской волны, распространяющейся вдоль оси х, имеет вид (см. § 154) 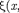t) = A cos - илив комплекснойзаписи 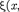t)— Следовательно, плоская волна де Бройля имеет вид

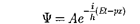(217.2)

(учтено, что — 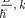= — ). В квантово й

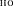показатель экспоненты берут со знаком « — », поскольку физический смысл имеет только |Ф|2, то это несуществен- но. Тогда

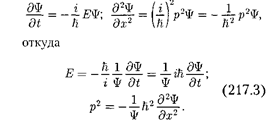Используя взаимосвязь между энерги- ей Е и импульсом 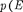= -—) и подставляя

2т

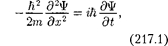выражения (217.3), получим дифференци- альное уравнение

которое совпадает с уравнением для случая U— О (мы рассматривали свободную частицу).

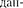Если частица движется в силовом поле, характеризуемом потенциальной энерги- ей U, то полная энергия Е складывается из кинетической и потенциальной энергий. Проводя аналогичные рассуждения и ис- пользуя взаимосвязь между 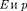('для

V2

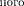
случая = Е -U), придем к диффе- ренциальному уравнению, совпадающему с (217.1).

Приведенные рассуждения не долж- ны восприниматься как вывод уравне- ния Шредингера. Они лишь поясняют, как можно прийти к этому уравнению. Доказательством правильности уравне- ния Шредингера является согласие с опытом тех выводов, к которым приводит.

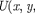Уравнение (217.1) является общим уравнением Шредингера. Его также называют уравнением Шредингера, зависящим от времени. Для многих физических явлений, происходящих в микромире, уравнение (217.1) можно упростить, исключив зависимость 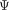времени, иными словами, найти урав- нение Шредингера для стационарных состояний — состояний с фиксирован- ными значениями энергии. Это возмож- но, если силовое поле, в котором час- тица движется, стационарно, т. е. функ- ция U= z) не зависит явно от вре- мени и имеет смысл потенциальной энергии.

В данном случае решение уравнения Шредингера может быть представлено в виде произведения двух функций, одна из которых есть функция только координат, другая — только времени, причем зависимость от времени выража-

ется множителем е" = е , так что

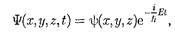(217.4)

где Е — полная энергия частицы, посто- янная в случае стационарного поля. Подставляя (217.4) в (217.1), получим

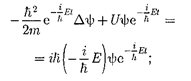
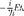
откуда после деления па общий множи- тель е соответствующих преобра-

зовании придем к уравнению, опреде- ляющему функцию

Уравнение урав-

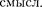нением Шредингера для стационар- ных состояний. В это уравнение в ка- честве параметра входит полная энер- гия Е частицы. В теории дифференци- альных уравнений доказывается, что подобные уравнения имеют бесчислен- ное множество решений, из которых по- средством наложения граничных усло- вий отбирают решения, имеющие фи- зический

Для уравнения Шредингера такими условиями являются условия регуляр- ности волновых функций: волновые функции должны быть конечными, од- нозначными и непрерывными вместе со своими первыми производными.

Таким образом, реальный физичес- кий смысл имеют только такие реше- ния, которые выражаются регулярны- ми функциями 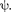Но регулярные реше- ния имеют место не при любых значе- ниях параметра Е, а лишь при опреде- ленном их наборе, характерном для дан- ной задачи. Эти значения энергии на- зываются собственными. Решения же, которые соответствуют собственным значениям энергии, называются соб- ственными функциями. Собственные значения Е могут образовывать как не- прерывный, так и дискретный ряд. В пер- вом случае говорят о непрерывном, или сплошном, спектре, во втором — о дис- кретном спектре.

§ 218. Принцип причинности в квантовой механике

Из соотношения неопределенностей часто делают вывод о неприменимости

принципа причинности к явлениям, происходящим в микромире. При этом основываются на следующих соображе- ниях. В классической механике, соглас- но принципупричинности— принци- пу классического детерминизма, поизвестному состоянию системы в неко- торый момент времени (полностью оп- ределяется значениями координат и импульсов всех частиц системы) и си- лам, приложенным к ней, можно абсо- лютно точно задать ее состояние в лю- бой последующий момент. Следова- тельно, классическая физика основыва- ется на следующем понимании причин- ности: состояние механической систе- мы в начальный момент времени с из- вестным законом взаимодействия час- тиц есть причина, а ее состояние в пос- момент — следствие.

С другой стороны, микрообъекты не могут иметь одновременно и опреде- ленную координату, и определенную соответствующую проекцию импульса [задаются соотношением неопределен- ностей 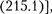поэтому и делается вы- вод о том, что в начальный момент вре- мени состояние системы точно не оп- ределяется. Если же состояние системы не определенно в начальный момент времени, то не могут быть предсказаны и последующие состояния, т. е. наруша- ется принцип причинности.

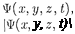Однако никакого нарушения прин- ципа причинности применительно к микрообъектам не наблюдается, по- скольку в квантовой механике понятие состояния микрообъекта приобретает совершенно иной смысл, чем в класси- ческой механике. В квантовой меха- нике состояние микрообъекта полнос- тью определяется волновой функцией квадрат модуля которой

2 задает плотность вероятно- сти нахождения частицы в точке с ко- ординатами х, у, z.

В свою очередь, волновая функция 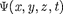удовлетворяет уравнению

Шредингера 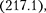содержащему пер- вую производную функции Ф по време- ни. Это же означает, что задание функ- ции 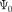(для момента времени 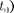опре- деляет ее значение в последующие мо- менты. Следовательно, в квантовой ме- ханике начальное состояние 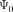есть причина, а состояние Ф в последующий момент — следствие. Это и есть форма принципа причинности в квантовой механике, т.е. задание функции 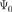пре- допределяет ее значения для любых последующих моментов. Таким обра- зом, состояние системы микрочастиц, определенное в квантовой механике, однозначно вытекает из предшествую- щего состояния, как того требует прин- цип причинности.

§219. Движение свободной частицы

Свободнаячастица — частица,дви- жущаяся в отсутствие внешних полей. Так как на свободную (пусть она движется вдоль оси х) силы не дей- ствуют, то потенциальная энергия час- тицы U(x) = const и ее можно принять равной нулю. Тогда полная энергия ча- стицы совпадает с ее кинетической энергией. В таком случае уравнение Шредингера (217.5) для стационарных состояний примет вид

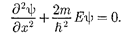(219.1)

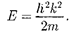Прямой подстановкой можно убе- диться в том, что частным решением уравнения (219.1) является функция 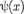— 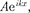где А = const и к = const, с собственным значением энергии

(219.2)

Функция 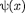= = 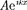представляет собой только координат- ную часть волновой функции 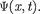Поэтому зависящая от времени волно- вая функция, согласно (217.4),

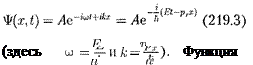
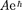(219.3) представляет собой плоскую монохроматическую волну де Бройля [см. (217.2)].

Извыражения (219.2) следует, что зависимость энергии от импульса

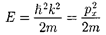
оказывается обычной для нерелятиви- стских частиц. Следовательно, энергия свободной частицы может принимать любые значения (так как волновое чис- ло к может принимать любые положи- тельные значения), т. е. энергетический спектр свободной частицы является непрерывным.

Таким образом, свободная квантовая частица описывается плоской монохро- матической волной де Бройля. Этому соответствует не зависящая от време- ни плотность вероятности обнаружения частицы в данной точке пространства

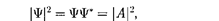
т. е. все положения свободной частицы в пространстве являются равновероят- ными.

§ 220. Частица в одномерной прямоугольной «потенциальной яме» с бесконечно высокими

«стенками»

Проведем качественный анализ ре- шений уравнения Шредингера приме-

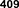
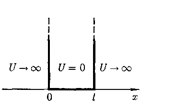Рис. 299

где

(220.3)

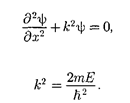(220.4)

нительно к частице водномерной пря- моугольной «потенциальной яме» с бесконечно высокими «стенками». Та- кая «яма» описывается потенциальной энергией вида (для простоты принима- ем, что частица движется вдоль оси х)

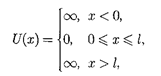
где 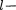ширина «ямы», аэнергия отсчи- тывается от ее дна (рис. 299).

Уравнение Шредингера (217.5) для стационарных состояний в случае одно- мерной задачи запишется в виде

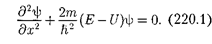
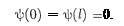По условию задачи (бесконечно вы- сокие «стенки»), частица не проникает за пределы «ямы», поэтому вероятность ее обнаружения (а следовательно, и вол- новая функция) за пределами «ямы» равна нулю. На границах «ямы» (при х— 0 и х = 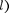непрерывная волновая функция также должна обращаться в нуль. Следовательно, граничные усло- вия в данном случае имеют вид

(220.2)

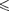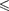
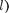В пределах «ямы» (0 х урав- нение Шредингера (220.1) сведется к уравнению

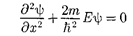Общее решение дифференциально- го уравнения (220.3):

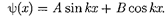
Так как по (220.2) 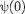= 0, то В = 0.

Тогда

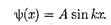(220.5)

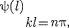
Условие (220.2) 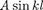= 0 выполняется только при где п — целые числа, т. е. необходимо, чтобы

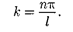(220.6)

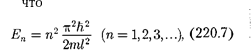Из выражений (220.4) и (220.6) сле- дует,

т. е. стационарное уравнение Шредин- гера, описывающее движение частицы в «потенциальной яме» с бесконечно высокими «стенками», удовлетворяет- ся только при собственных значени- ях 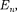зависящих от целого числа п. Следовательно, энергия 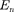частицы в

«потенциальной яме» с бесконечно вы- сокими «стенками» принимает лишь определенныедискретныезначения,т.е. квантуется.

Квантованные значения энергии 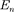называются уровнями энергии, а чис- ло п, определяющее энергетические уровни частицы, называется главным квантовым числом. Таким образом, микрочастица в «потенциальной яме» с бесконечно высокими «стенками» может находиться только на определен- ном энергетическом уровне 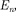или, как говорят, частица находится в квантовом

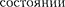п.

Подставив в (220.5) значение к из (220.6), найдем собственные функции:

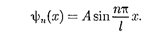Постоянную интегрирования А най- дем из условия нормировки (216.3), которое для данного случая запишется в виде

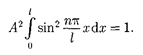
Врезультате интегрирования полу-

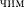А — 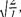асобственные функции будут иметь вид

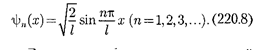
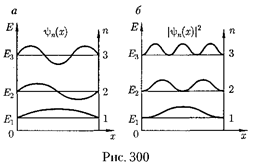
I рафики собственных функции (220.8), соответствующие уровням

энергии (220.7) при п=1,2, 3, приведе- ны на рис. 300, а. На рис. 300, б изобра- жена плотность вероятности обнаруже- ния частицы на различных расстояни- ях от «стенок» ямы, равная =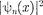

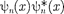для п= 1, 2 и 3. Из рисун- ка следует, что, например, в квантовом состоянии с п = 2 частица не может на- ходиться в середине «ямы», в то время как одинаково часто может пребывать в ее левой и правой частях. Такое пове- дение частицы указывает на то, что представления о траекториях частицы в квантовой механике несостоятельны. Из выражения (220.7) вытекает, что энергетический интервал между двумя

соседними уровнями равен

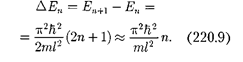Например, для электрона при раз- мерах ямы — 10"1 м (свободные элек-

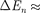
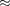троны в металле) 10 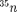Дж

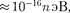
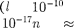
т. е. энергетические уровни расположены столь тесно, что спектр практически можно считать непрерыв- ным. Если же размеры ямы соизмери- мы с атомными м), то для электрона 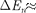Дж 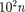эВ, т.е. получаются явно дискретные зна- чения энергии (линейчатый спектр).

Таким образом, применение уравне- ния Шредингера к частице в «потенци- альной яме» с бесконечно высокими

«стенками» приводит к квантованным значениям энергии, в то время как клас- сическая механика на энергию этой ча- стицы никаких ограничений не накла- дывает.

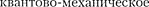Кроме того,

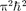рассмотрение данной задачи приводит к выводу, что частица «в потенциаль- ной яме» с бесконечно высокими «стен- ками» не может иметь энергию меньше

минимальной, равной [см. (220.7)].

Наличие отличной от нуля мини- мальной энергии не случайно и выте- кает из соотношения неопределеннос- тей. Неопределенность координаты Ах частицы в «яме» шириной 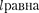Ах= 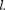Тогда, согласно соотношению неопре- деленностей 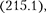импульс не может иметь точное, в данном случае нулевое, значение. Неопределенность импульса

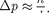Такому разбросу значений

V

импульса соответствует кинетическая энергия

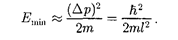
Все остальные уровни (п >1) име- ют энергию, превышающую это мини- мальное значение.

Изформул (220.9) и (220.7) следу- ет, что при больших квантовых числах

т. е. соседние уровни расположены тес- но: тем теснее, чем больше п. Если п очень велико, то можно говорить о практически непрерывной последова- тельности уровней и характерная осо- бенность квантовых процессов — диск- ретность — сглаживается. Этот резуль- тат является частным случаем принци- па соответствия Бора (1923), соглас- но которому законы квантовой механи- ки должны при больших значениях квантовых чисел переходить в законы классической физики.

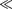Более общая трактовка принципа соответствия: всякая новая, более общая теория, являющаяся развитием классической, не отвергает ее полнос- тью, а включает в себя классическую теорию, указывая границы ее примене- ния, причем в определенных предель- ных случаях новая теория переходит в старую. Так, формулы кинематики и динамики специальной теории относи- тельности переходят при v с в форму- лы механики Ньютона. Например, хотя гипотеза да Бройля приписывает вол- новые свойства всем телам, но в тех слу- чаях, когда мы имеем дело с макроско- пическими телами, их волновыми свой- ствами можно пренебречь, т.е. приме- нять классическую механику Ньютона.

§ 221. Прохождение частицы сквозь потенциальный барьер.

Туннельный эффект

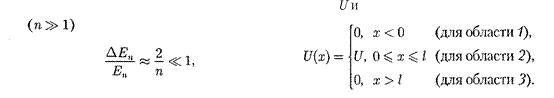
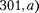
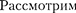простейший потенци- альный барьер прямоугольной формы (рис. для одномерного (по оси 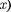движения частицы. Для потенциально- го барьера прямоугольной формы вы- сотой шириной /можем записать

При данных условиях задачи клас- сическая частица, обладая энергией Е, либо беспрепятственно пройдет над ба- рьером (при Е > U), либо отразится от него (при Е < U) будет двигаться в обратную сторону, т.е. она не может проникнуть сквозь барьер. Для микро- частицы, даже при Е > U, имеется от- личная от нуля вероятность, что части- ца отразится от барьера и будет двигать- ся в обратную сторону. При Е <U име- ется также отличная от нуля вероят- ность, что частица окажется в области х> 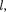т.е. проникнет сквозь барьер. По- добные, казалось бы, парадоксальные выводы следуют непосредственно из решения уравнения Шредингера, опи-

412

сывающего движение микрочастицы при условиях данной задачи.

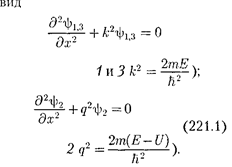
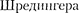Уравнение (217.5) для стационарных состояний для каждой из выделенных рис. 301, а области име- ет

(для областей

(для области

Общие решения этих дифференци- альных уравнений:

Решение (221.3) содержит также волны (после умножения на временной множитель), распространяющиеся в обе стороны. Однако в области 3 име- ется только волна, прошедшая сквозь барьер и распространяющаяся слева направо. Поэтому коэффициент 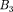формуле (221.3) следует принять рав- ным нулю.

В области 2 решение зависит от со- отношений E>U или Е <U. Физичес- кий интерес представляет случай, ког- да полная энергия частицы меньше вы- соты потенциального барьера, посколь- ку при Е 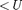законы классической фи- зики однозначно не разрешают части- це проникнуть сквозь барьер. В данном случае, согласно 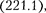q = 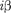— мни- мое число, где

(для области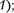

=

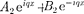
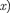(для области 2);

(221.2)

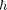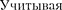значение q и 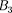0, полу- чим решения уравнения Шредингера для трех областей в следующем виде:

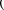
(для области 3).

Вчастности, для области 1 полная волновая функция, согласно (217.4), будет иметь вид

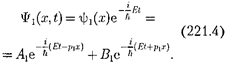В этом выражении первое слагаемое представляет собой плоскую волну типа (219.3), распространяющуюся в положительном направлении оси х (со- ответствует частице, движущейся в сто- рону барьера), а второе — волну, рас- пространяющуюся в противоположном направлении, т. е. отраженную от барь- ера (соответствует частице, движущей- ся от барьера налево).

(для области 3).

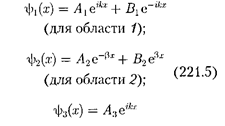
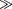В области 2 функция 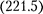уже не соответствует плоским волнам, распро- страняющимся в обе стороны, посколь- ку показатели степени экспонент не мнимые, а действительные. Можно по- казать, что для частного случая высо- кого и широкого барьера, когда 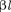1,

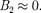
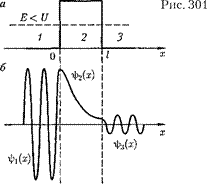
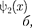Качественный характер функци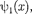й и 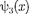иллюстрируется на рис. 301, откуда следует, что волно-

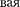функция не равна нулю и внутри ба- рьера, а в области 3, если барьер не очень широк, будет опять иметь вид волн де Бройля с тем же импульсом, т. е. с той же частотой, но с меньшей ампли- тудой. Следовательно, получили, что частица имеет отличную от нуля веро- ятность прохождения сквозь потенци- альный барьер конечной ширины.

Таким образом, квантовая механика приводит к принципиально новому спе- цифическому квантовому явлению, по- лучившему название туннельного эф- фекта, в результате которого микро- объект может «пройти» сквозь потен- циальный барьер.

Для описания туннельного эффек- та используют понятие коэффициента прозрачности D потенциального барье- ра, определяемого как отношение плот- ности потока прошедших частиц к плотности потока падающих. Можно показать, что

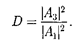
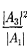Для того чтобы найти отношение

, необходимо воспользоваться ус-

ловиями непрерывности и 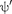на гра- ницах барьера х 0 и х = (рис.

(221.6)

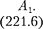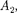
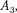
Эти четыре условия дают возмож- ность выразить коэффициенты 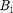и 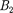через Совместное решение уравнений для прямоугольного потенциального барьера дает (в предпо- ложении, что коэффициент прозрачно- сти мал по сравнению с единицей)

(221.7)

где 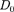— постоянный множитель, кото- рый можно приравнять единице; U — высота потенциального барьера; Е — энергия частицы; 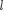— ширина барьера.

Из выражения (221.7) следует, что D сильно зависит от массы т частицы, ширины / барьера и от (U — 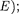чем шире барьер, тем меньше вероятность прохождения сквозь него частицы.

Для потенциального барьера произ- вольной формы (рис. 302), удовлетво- ряющей условиям так называемого ква- зиклассического приближения (доста- точно гладкая форма кривой), имеем

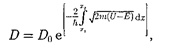где U= U(x).

С классической точки зрения про- хождение частицы сквозь потенциаль- ный барьер при Е <U невозможно, так как частица, находясь в области барье- ра, должна была бы обладать отрица- тельной кинетической энергией. Тун- нельный эффект является специфиче- ским квантовым эффектом.

Прохождение частицы сквозь об- ласть, в которую, согласно законам клас- сической механики, она не может про- никнуть, можно пояснить соотношени- ем неопределенностей. Неопределен- ность импульса Ар на отрезке Ах = 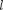со- ставляет Ар > —. Связанная с этим раз- бросом в значениях импульса кинети-

302

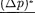ческая энергия может оказаться

2т

достаточной для того, чтобы полная

энергия частицы оказалась больше по- тенциальной.

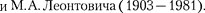Основы теории туннельных перехо- дов заложены в работах Л. И. Мандель- штама

Туннельное прохождение сквозь потен- циальный барьер лежит в основе мно- гих явлений физики твердого тела (на- пример, явления в контактном слое на границе двух полупроводников), атом- ной и ядерной физики (например, распад, протекание термоядерных реак- ций).

§ 222. Линейный гармонический осциллятор

В квантовой механике

Линейный гармонический осцил- лятор — система, совершающая одно- мерное движение под действием квази- упругой силы, — является моделью, ис- пользуемой во многих задачах класси- ческой и квантовой теории (см. § 142). Пружинный, физический и математи- ческий маятники — примеры класси- ческих гармонических осцилляторов.

Потенциальная энергия гармони- ческого осциллятора [см. (141.5)] равна

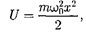(222.1)

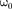где — собственная частота колебаний осциллятора; т — масса частицы.

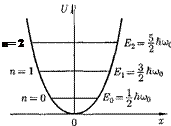
Зависимость (222.1) имеет вид пара- болы (рис. 303), т.е. «потенциальная яма» в данном случае является парабо- лической.

Амплитуда малых колебаний клас- сического осциллятора определяется его полной энергией Е (см. рис. 17).

303

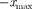
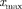В точках с координатами 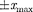полная энергия Е равна потенциальной энер- гии. Поэтому с классической точки зре- ния частица не может выйти за преде- лы области 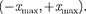Такой выход означал бы, что ее потенциальная энер- гия больше полной, что абсурдно, так как приводит к выводу, что кинетичес- кая энергия отрицательна. Таким обра- зом, классический осциллятор находит- ся в «потенциальной яме» с координа- тами 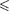х 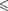«без права выхо- да» из нее.

Гармонический осциллятор в кван- товой механике — квантовый осцил- лятор — описывается уравнением 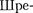дингера 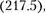учитывающим выраже- ние (222.1) для потенциальной энергии. Тогда стационарные состояния кванто- вого осциллятора определяются урав- нением Шредингера вида

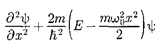= 0, (222.2)

где Е — полная энергия осциллятора. В теории дифференциальных урав-

нений доказывается, что уравнение (222.2) решается только при собствен- ных значениях энергии

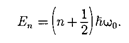(222.3)

Формула (222.3) показывает, что энергия квантового осциллятора может

иметь лишь дискретные значения, т. е. квантуется. Энергия ограничена сни- зу отличным от нуля, как и для прямо- угольной «ямы» с бесконечно высоки- ми «стенками» (см. § 220), минималь- ным значением энергии 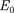= 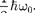Су-

ществование минимальной энергии — она называется энергией нулевых ко- лебаний — является типичной для кван- товых систем и представляет собой пря- мое следствие соотношения неопреде- ленностей.

Наличие нулевых колебаний означа- ет, что частица не может находиться на дне «потенциальной ямы» (независимо от формы ямы). В самом деле, «падение на дно ямы» связано с обращением в нуль импульса частицы, а вместе с тем и его неопределенности. Тогда неопреде- ленность координаты становится сколь угодно большой, что противоречит, в свою очередь, пребыванию частицы в

«потенциальной яме».

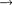Вывод о наличии энергии нулевых колебаний квантового осциллятора про- тиворечит выводам классической тео- рии, согласно которой наименьшая энергия, которую может иметь осцил- лятор, равна нулю (соответствует поко- ящейся в положении равновесия части- це). Например, согласно выводам клас- сической физики при Т = 0 энергия колебательного движения атомов кри- сталла должна была бы обращаться в нуль. Следовательно, должно исчезать и рассеяние света, обусловленное коле- баниями атомов. Однако эксперимент показывает, что интенсивность рассея- ния света при понижении температуры не равна нулю, а стремится к некоторо- му предельному значению, указываю- щему на то, что при Т 0 колебания атомов в кристалле не прекращаются. Это является подтверждением наличия нулевых колебаний.

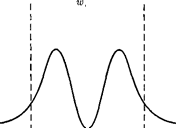
о

Рис. 304

Из формулы (222.3) также следует, что уровни энергии линейного гармо- нического осциллятора расположены на одинаковых расстояниях друг от друга (см. рис. 303), а именно расстоя- ние между соседними энергетическими уровнями равно 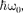причем минималь- ное значение энергии =

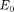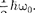
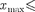
Строгое решение задачи о квантовом осцилляторе приводит еще к одному значительному отличию от классиче