Прямолинейное распространение света
Принцип Гюйгенса— Френеля в рам- ках волновой теории должен был отве- тить на вопрос о прямолинейном рас- пространении света. Френель решил эту задачу, рассмотрев взаимную интер- ференцию вторичных волн и применив прием, получивший название метода зон Френеля.
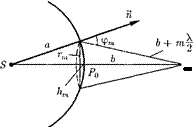
Найдем в произвольной точке плитуду световой волны, распространя- ющейся в однородной среде из точеч- ного источника S монохроматического света (рис. 260). Согласно принципу Гюйгенса— Френеля, заменим действие источника S действием воображаемых источников, расположенных на вспомо- гательной поверхности 
поверхностью фронта волны, идущей из S (поверхность сферы с центром S).
Френель предложил разбить волно- вую поверхность Ф па кольцевые зоны
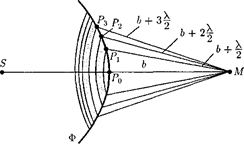
Рис 260
такого размера, чтобы расстояния от краев зоны до М отличались на —, т.е.
= =
... 
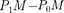
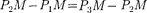Подобное разбиение фронта волны на зоны можно выполнить, про- ведя с центром в точке М сферы радиу- сами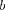 
+ — ,6 + 2 — 
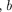+ 3 —, .... Так как от соседних зон проходят до
точки 
отличающиеся на
—, то в точку 
приходят в противо- положной фазе и при наложении эти ко- лебании будут взаимно ослаблять друг друга. Поэтому амплитуда результиру- ющего светового колебания в точке М
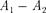
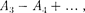A + (177.1)
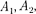где ... — амплитуды колебаний, возбуждаемых 1-й, 2-й, ... зонами.
Для оценки амплитуд колебаний найдем площади зон Френеля. Пусть внешняя граница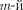 
зоны выделяет на волновой поверхности сферический
м
Рис. 261
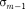сегмент высоты 
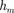(рис. 261). Обозна- чив площадь этого сегмента через найдем, что площадь m-й зоны Френе- ля равна 
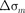= - где - площадь сферического сегмента, выде- ляемого внешней границей (т — 1)-й зоны. Из рисунка следует, что
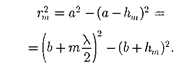(177.2)
После элементарных преобразова- ний, учитывая, что X а и X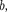 
по- лучим
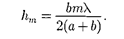(177.3)
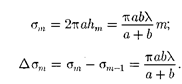Площадь сферического сегмента и площадь m-й зоны Френеля соответ- ственно равны
(177.4)
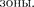Выражение (177.4) не зависит от т, следовательно, при не слишком боль- ших т площади зон Френеля одинако- вы. Таким образом, построение зон Френеля разбивает волновую поверх- ность сферической волны на равнове- ликие
Согласно предположению Френеля, действие отдельных зон в точке М тем меньше, чем больше угол (см. рис.
261) между нормалью п поверхности зоны и направлением на М, т. е. действие зон постепенно убывает от центральной (около 
к периферическим. Кроме того, интенсивность излучения в направ- лении точки М уменьшается с ростом т. и вследствие увеличения расстояния от зоны до точки М. Следовательно,
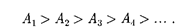
Общее число зон Френеля, умещаю- щихся на полусфере, очень велико; на- пример, при а = Ъ = 10см и X = 0,5мкм
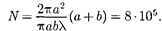Поэтому в ка-
честве допустимого приближения мож- но считать, что амплитуда колебания 
от некоторой m-й зоны Френеля равна среднему арифметическому от ампли- туд примыкающих к ней зон, т. е.
 |
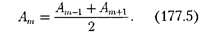Тогда выражение (177.1) можно за- писать в виде
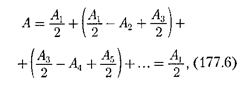
так как выражения, стоящие в скобках, согласно (177.5), равны нулю, а остав- шаяся часть от амплитуды последней зоны ничтожно мала.
Таким образом, амплитуда резуль- тирующих колебаний в произвольной точке М определяется как бы действи- ем только половины центральной зоны Френеля. Следовательно, действие всей волновой поверхности на точку М сводится к действию ее малого участ- ка, меньшего центральной зоны.
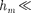
Если в выражении (177.2) положим, что высота сегмента (при не слишком больших т), тогда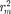 
= 
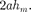Подставив сюда значение (177.3), най- дем радиус внешней границы m-й зоны Френеля:
Пр и = Ь — 10 и X 0,5 мк м радиус первой (центральной) зоны = 0,158 мм.
Следовательно, распространение света от S М происходит так, будто свето- вой поток распространяется внутри очень узкого канала вдоль SM, т. е. пря- молинейно. Таким образом, принцип Гюйгенса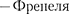 
позволяет объяс- нить прямолинейное распространение света в однородной среде.
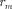
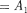Правомерность деления волнового фронта на зоны Френеля подтвержде- на экспериментально. Для этого ис- пользуются зонные пластинки — в про- стейшем случае стеклянные пластинки, состоящие из системы чередующихся прозрачных и непрозрачных концент- рических колец, построенных по прин- ципу расположения зон Френеля, т.е. с радиусами зон Френеля, определя- емыми выражением (177.7) для задан- ных значений а, Ь X (т 0, 2, 4,... для прозрачных и т — 1, 3, 5,... для непроз- рачных колец). Если поместить зонную пластинку в строго определенном мес- те (на расстоянии а от точечного источ- ника и на расстоянии Ь от точки наблю- дения на линии, соединяющей эти две точки), то для света длиной волны 
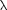она перекроет четные зоны и оставит сво- бодными нечетные, начиная с централь- ной. В результате этого результирую- щая амплитуда А + 
+ 
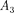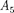+ ... должна быть больше, чем при полнос- тью открытом волновом фронте. Опыт подтверждает эти выводы: зонная пла- стинка увеличивает освещенность в точке М,действуяподобнособирающей линзе.
§ 178. Дифракция Френеля на круглом отверстии и диске
Дифракцию разделяют на два типа — в зависимости от расстояний от источ- ника и точки наблюдения (экрана) до препятствия, расположенного на пути
распространения света. Первый тип дифракции относится к случаю, когда на препятствие падает сферическая или плоская волна, а дифракционная кар- тина наблюдается на экране, находя- щемся за препятствием па конечном от него расстоянии. Дифракционные яв- ления этого типа впервые изучены Фре- нелем и называются дифракцией Фре- неля (или дифракцией в сходящихся лучах).
При рассмотрении этого типа диф- ракции воспользуемся гипотезой Фре- неля (см. § 176), согласно которой часть волнового фронта, закрытая экраном, действует вообще, а незакрытые уча- стки волнового фронта действуют, как в случае отсутствия экрана. Это при- ближение вполне допустимо в случаях, когда размеры отверстия значительно больше длины волны X, так как влия- ние экрана существенно лишь в непос- редственной близости от его края (на расстояниях, сравнимых с длиной вол-
ны X).
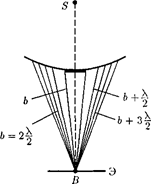
1. Дифракция на круглом отвер- стии.Сферическая волна, распростра- няющаяся из точечного источника S, встречает на своем пути экран с круг- лым отверстием. Дифракционную кар- тину наблюдаем на экране Э в точке В, лежащей на линии, соединяющей S с центром отверстия (рис. 262). Экран па- раллелен плоскости отверстия и нахо-
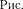262
дится от него на расстоянии Ь. Разобь- ем открытую часть волновой поверхно- сти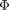 
на зоны Френеля. Вид дифракци- онной картины зависит от числа зон Френеля, укладывающихся на откры- той части волновой поверхности в плос- кости отверстия. Амплитуда результи- рующего колебания, возбуждаемого в точке В всеми зонами [см. (177.1) и (177.6)],
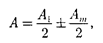
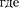знак «+» соответствует нечетным т
и «—» — четным т.
Если отверстие открывает нечетное число зон Френеля, то амплитуда (ин- тенсивность) в точке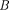 
будет больше, чем при свободном распространении волны, если четное, то амплитуда (ин- тенсивность) будет равна пулю.
Если отверстие открывает одну зону Френеля, то в точке В амплитуда А =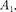 
т.е. вдвое больше, чем в отсутствие не- прозрачного экрана с отверстием (см.
§ 177). Интенсивность света больше со- ответственно в четыре раза.
Если отверстие открывает две зоны Френеля, то их действия в точке В прак- тически уничтожат друг друга из-за ин- терференции. Таким образом, дифрак- ционная картина от круглого отверстия вблизи точки В будет иметь вид
263
дующихся темных и светлых колец с центрами в точке В (если т четное, то в центре будет темное кольцо, если т нечетное — то светлое кольцо), причем интенсивность в максимумах убывает с расстоянием от центра картины.
Расчет амплитуды результирующе- го колебания на внеосевых участках экрана более сложен, так как соответ- ствующие им зоны Френеля частично перекрываются непрозрачным экра- ном. Если отверстие освещается не мо- нохроматическим, а белым светом, то кольца окрашены.
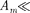Число зон Френеля, открываемых отверстием, зависит от его диаметра. Если он большой, то 
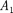и резуль-
тирующая амплитуда А = —, т.е. та-
кая же, как и при полностью открытом волновом фронте. В данном случае дифракции не наблюдается, свет рас- пространяется, как и в отсутствие круг- лого отверстия, прямолинейно.
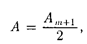
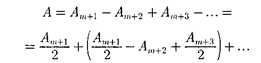
2. Дифракция на диске. Сферичес- кая волна, распространяющаяся от то- чечного источника S, встречает на сво- ем пути непрозрачный диск. Дифракци- онную картину наблюдаем на экране Э в точке В, лежащей на линии, соединя- ющей S с центром диска (рис. 263). В данном случае закрытый диском уча- сток волнового фронта надо исключить из рассмотрения и зоны Френеля стро- ить, начиная с краев диска. Пусть диск закрывает т первых зон Френеля. Тог- да амплитуда результирующего колеба- ния в точке В равна
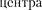так как выражения, стоящие в скобках, равны нулю. Следовательно, в точке 
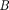всегда наблюдается интерференцион- ный максимум (светлое пятно), соот- ветствующий половине действия пер- вой открытой зоны Френеля. Цент- ральный максимум окружен концент- рическими с ним темными и светлыми кольцами, а интенсивность в максиму- мах убывает с расстоянием от картины.
С увеличением диаметра диска пер- вая открытая зона Френеля удаляется от точки В увеличивается угол (см. рис. 261) между нормалью к поверхно- сти этой зоны и направлением на точ- ку В. В результате интенсивность цен- трального максимума с увеличением размеров диска уменьшается. 
боль- ших размерах диска за ним наблюдает- ся тень, вблизи границ которой имеет место весьма слабая дифракционная картина.
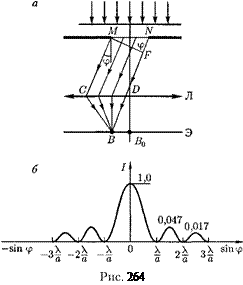
этого практически достаточно, чтобы длина щели была значительно больше ее ширины). Пусть плоская монохрома- тическая световая волна падает нор- мально плоскости узкой щели шири- ной а (рис. 264, а). Оптическая разность хода между крайними лучами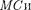 
ND, идущими от щели в произвольном на- правлении
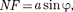A (179.1)
где F — основание перпендикуляра, опущенного из точки М на луч ND.
Согласно принципу Гюйгенса — Френеля, каждая точка щели является источником вторичных волн. Откры- тую часть волновой поверхности в плоскости щели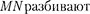 
на зоны Френеля, имеющие вид полос, парал- лельных ребру М щели. Ширина каж- дой зоны выбирается так, чтобы раз- ность хода от краев этих зон была рав-
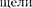
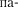на —2, т. е. всего на ширине умес-
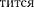
Х/2
зон. 1 ак как свет на щель
§ 179. Дифракция Фраунгофера
На одной щели
Второй тип дифракции — дифрак- ция 
(или дифракция в параллельных лучах) наблюдается в том случае, когда источник света и точ- ка наблюдения бесконечно от препятствия, вызвавшего дифракцию. Чтобы этот тип дифракции осущест- вить, достаточно точечный источник света поместить в фокусе собирающей линзы, а дифракционную картину ис- следовать в фокальной плоскости вто- рой собирающей линзы, установленной за препятствием.
Рассмотрим дифракцию Фраунго- фера от бесконечно длинной щели (для
дает нормально, то плоскость щели со-
(1787-1826) немецкий физик.
впадает с волновым фронтом; следова- тельно, все точки волнового фронта в плоскости щели будут колебаться в одинаковой фазе. Амплитуды вторич- ных волн в плоскости щели будут рав- ны, так как выбранные зоны Френеля имеют одинаковые площади и одинако- во наклонены к направлению наблюде- ния.
Из выражения (179.1) вытекает, что число зон Френеля, укладывающихся на ширине щели, зависит от угла От числа зон Френеля, в свою очередь, за- висит результат наложения всех вто- ричных волн. Из приведенного постро- ения следует, что при интерференции света от каждой пары соседних зон Фре- неля амплитуда результирующих коле- баний равна нулю, так как колебания от каждой пары соседних зон взаимно га- сят друг друга. Следовательно, если число зон Френеля четное, то
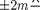
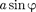= (m = 1,2,3, ...), (179.2)
и в точке В наблюдается дифракцион- ный минимум (полная темнота), если же число зон Френеля нечетное, то
 |
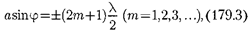и наблюдается дифракционный мак- симум, соответствующий действию од- ной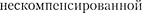 
зоны Фре-
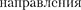неля. Отметим, что в направлении = О щель действует как одна зона Френе- ля, и в этом направлении свет распрос- траняется с наибольшей интенсивнос- тью, т.е. в точке 
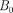наблюдается цент- ральный дифракционный максимум. Из условий (179.2) и (179.3) можно найти на точки экрана, в которых амплитуда (а следовательно, и интенсивность) равна нулю 
=
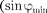= ) или максимальна 
=
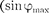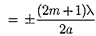). Распределение сивности на экране, получаемое вслед- ствие дифракции (дифракционный спектр), приведено на рис. 264, б. Рас- четы показывают, что интенсивности в центральном и последующих макси- мумах относятся как 1 : 0,047 : 0,017 : 0,0083 : ..., т. е. основная часть световой энергии сосредоточена в центральном максимуме. С уменьшением ширины щели центральный максимум расширя-
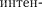ется [согласно (179.2) возрастают углы Ф = 
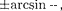которые соответствуют
минимумам первого порядка, ограни- чивающим центральный максимум]; при этом яркость его уменьшается. Все сказанное относится и к другим макси- мумам.
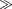С увеличением ширины щели 
> 
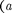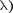дифракционные полосы становятся уже и ярче, а число полос больше. При а X вцентреполучаетсярезкоеизоб- ражение источника света (имеет мес- то прямолинейное распространение света).
При а = \ (что соответствует sin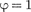 
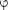= —) центральный максимум рас- плывается в бесконечность и экран ос- вещен равномерно. Отметим, что при а 
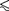X приближенный метод Френеля не применяют, так как волновое поле в плоскости щели нельзя отождествлять с неискаженным полем падающей вол- ны. В данном случае необходимо стро- гое решение задачи с использованием уравнений Максвелла.
Положение дифракционных макси- мумов зависит от длины волны X, по- этому рассмотренная выше дифракци- онная картина имеет место лишь для монохроматического света. При осве- щении щели белым светом централь- ный максимум наблюдается в виде бе- лой полоски; он общий для всех длин
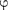
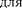
волн (при = 0 разность хода равна пулю для всех X). Боковые максимумы радужно окрашены, так как условие максимума при любых га различно разных X. Таким образом, справа сле- ва от центрального максимума наблю- даются максимумы первого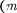 
— 1), второго (га = 2) и других порядков, об- ращенные фиолетовым краем к центру дифракционной картины. Однако они настолько расплывчаты, что отчетливо- го разделения различных длин волн с помощью дифракции на одной щели получить невозможно.
§ 180. Дифракция Фраунгофера на дифракционной решетке
Большое практическое значение имеет дифракция, наблюдаемая при прохождении света через одномерную дифракционную решетку — систему параллельных щелей равной
лежащих в одной плоскости и разделен- ных равными по ширине непрозрачны- ми промежутками. Рассматривая диф- ракцию Фраунгофера на щели, мы ви- дели, что распределение интенсивнос- ти на экране определяется направлени- ем дифрагированных лучей. Это озна- чает, что перемещение щели параллель- но самой себе влево или вправо не из- менит дифракционной картины. Следо- вательно, если перейти от одной щели ко многим (кдифракционной решетке), то дифракционные картины, создавае- мые каждой щелью в отдельности, бу- дут одинаковыми.
Дифракционная картина на решет- ке определяется как результат взаим- ной интерференции волн, идущих от всех щелей, т.е. в дифракционной ре- шетке осуществляется многолучевая интерференция когерентных дифраги-
пучков света, идущих от всех
щелей.
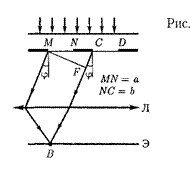
Рассмотрим дифракционную решет- ку. На рис. 265 для наглядности пока- заны только ее две соседние щели MN и CD. Если ширина каждой щели рав- на а, а ширина непрозрачных участков между щелями 
то величина d — а + Ь называется постоянной (периодом) дифракционнойрешетки. Пусть плос- кая монохроматическая волна падает нормально к плоскости решетки. Так как щели находятся друг от друга на одинаковых расстояниях, то разности хода лучей, идущих от двух соседних щелей, будут для данного направле- ния одинаковы в пределах всей диф- ракционной решетки:
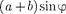Д = CF= = 
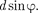(180.1)
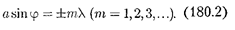
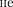Очевидно, что в тех направлениях, в которых ни одна из щелей не распрос- траняет свет, он будет распростра- няться и при двух щелях, т. е. прежние (главные) минимумы интенсивности будут наблюдаться в направлениях, оп- ределяемых условием (179.2):
Кроме того, вследствие взаимной ин- терференции световых лучей, посылае- мых двумя щелями, в некоторых направ- лениях они будут гасить друг друга, т.е. возникнут дополнительные миниму- мы. Очевидно, что эти дополнительные минимумы будут наблюдаться в тех на-
правлениях, которым соответствует
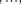
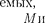разность хода 
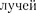— , 3 посыла- например, от крайних левых то-
чек С обеих щелей. Таким образом, с учетом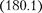 
условие дополнитель- ных минимумов:
 |
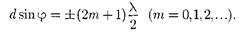Наоборот, действие одной щели бу- дет усиливать действие другой, если
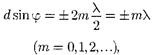(180.3)
т. е. между двумя главными максимума- ми располагается один дополнитель- ный минимум. Аналогично можно по- казать, что между каждыми двумя глав- ными максимумами при трех щелях располагается два дополнительных ми- нимума, при четырех щелях — три и т. д. Если дифракционная решетка состо-
ит из N щелей, то условием главных минимумов является условие (180.2), условием главных максимумов — усло- вие (180.3), а условием дополнитель- ных минимумов
т.е. выражение (180.3) задает условие
главных максимумов.
Таким образом, полная дифракци- онная картина для двух щелей опреде- ляется из условий:
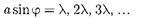
(главные минимумы);
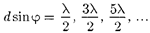
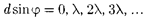(дополнительные минимумы);
(180.4)
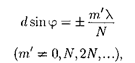
где т может принимать все целочис- ленные значения, кроме тех, при кото- рых условие (180.4) переходит в (180.3). Следовательно, в случае N щелей меж- дудвумя главнымимаксимумамираспо- лагается N — 1 дополнительных мини- мумов, разделенныхвторичнымимакси- мумами, создающими слабый фон.
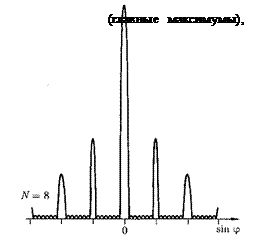
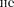Чем больше щелей N, тем большее количество световой энергии пройдет через решетку, тем больше минимумов образуется между соседними главными максимумами, а следовательно, более интенсивными и более острыми будут максимумы. На рис. 266 качественно представлена дифракционная картина от восьми щелей. Так как модуль 
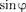может быть больше единицы, то из (180.3) следует, что число главных мак-
симумов
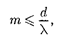
266
т. е. определяется отношением периода решетки к длине волны.
Положение главных максимумов зависит от длины волны \ [см. (180.3)].
Поэтому при пропускании через решет- ку белого света все максимумы, кроме центрального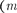 
= 0), разложатся в спектр, фиолетовая область которого будет обращена к центру дифракцион- ной картины, красная — наружу. Это свойство дифракционной решетки ис- пользуется для исследования спект- рального состава света (определения длин волн и 
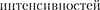всех мо- нохроматических компонентов), т.е. дифракционная решетка может быть использованакакспектральныйприбор, предназначенный для разложения све- та в спектр и измерения длин волн.
Дифракционные решетки, использу- емые в различных областях спектра, от- личаются размерами, формой, материа- лом поверхности, профилем штрихов и их частотой (от 6000 до 0,25 штрих/мм, что позволяет перекрывать область спектра от ультрафиолетовой его час- ти до инфракрасной). Например, сту- пенчатый профиль решетки позволяет концентрировать основную часть пада- ющей энергии в направлении одного определенного ненулевого порядка.
§ 181. Пространственная решетка. Рассеяние света
Дифракция света наблюдается не только на плоской одномернойрешет- ке (штрихи нанесены перпендикуляр- но некоторой прямой линии), по и на двумерной решетке (штрихи нанесе- ны во взаимно перпендикулярных на- правлениях в одной и той же плоско- сти).
Большой интерес представляет так- же дифракция на пространственных
{трехмерных) решетках — простран- ственных образованиях, в которых эле- менты структуры подобны по форме, имеют геометрически правильное и пе-
риодически повторяющееся располо- жение, а также постоянные (периоды) решеток, соизмеримые с длиной волны электромагнитного излучения. Иными словами, подобные пространственные образования должны иметь периодич- ность по трем, не лежащим в одной плоскости, направлениям.
В качестве пространственных диф- ракционных решеток могут быть ис- пользованы кристаллические тела, так как в них неоднородности (атомы, мо- лекулы, ионы) регулярно повторяются в трех направлениях.
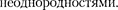Дифракция света может происхо- дить также в так называемых мутных средах — средах с явно выраженными оптическими К мут-
ным средам относятся аэрозоли (обла- ка, дым, туман), эмульсия, коллоидные растворы и т.д., т.е. такие среды, в ко- торых взвешено множество очень мел- ких частиц инородных веществ.
Свет, проходя через мутную среду, дифрагирует от беспорядочно располо- женных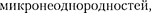 
давая
равномерное распределение интенсив-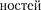 
по всем направлениям, не созда- вая какой-либо определенной дифрак- ционной картины. Происходит так на- зываемое рассеяние света в мутной среде. Это явление можно наблюдать, например, когда узкий пучок солнеч- ных лучей, проходя через запыленный воздух, рассеивается на пылинках и тем самым становится видимым.
Рассеяние света (как правило, сла- бое) наблюдается также и в чистых сре- дах, не содержащих посторонних час- тиц. Л. И. Мандельштам объяснил рас- сеяние света в средах нарушением их оптической однородности, при котором показатель преломления среды не по- стоянен, а меняется от точки к точке.
В дальнейшем польский физик М.Смолуховский (1872—1917)
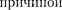зал, что рассеяния света мо- гут быть также флуктуации плотности, возникающие в процессе хаотического (теплового) движения молекул среды. Рассеяние света в чистых средах, обус- ловленное флуктуациями плотности, анизотропии или концентрации, назы- вается молекулярным рассеянием.
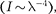Молекулярным рассеянием объяс- няется, например, голубой цвет неба. Согласно закону Д. Рэлея, интенсив- ность рассеянного света обратно про- порциональна четвертой степени дли- ны волны поэтому голубые и синие лучи рассеиваются сильнее, чем желтые и красные, обусловливая тем самым голубой цвет неба. По этой же причине свет, прошедший через значи- тельную толщу атмосферы, оказывает- ся обогащенным более длинноволно- вой частью спектра (сине-фиолетовая часть спектра полностью рассеивается) и поэтому при закате и восходе Солнце кажется красным. Флуктуации плотно- сти и интенсивность рассеяния света возрастают с увеличением температу- ры. Поэтому в ясный летний день цвет неба является более насыщенным по сравнению с таким же зимним днем.
§ 182. Дифракция
на пространственной решетке. Формула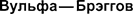 
Для наблюдения дифракционной картины необходимо, чтобы постоян- ная решетки была того же порядка, что и длина волны падающего излучения [см. (180.3)]. Кристаллы, являясь трех- мерными решетками (см. § 181), име- ют постоянную порядка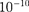 
м и, сле- довательно, непригодны для наблюде- ния дифракции в видимом свете (X
5 • 10~7м). М. Лауэ [немецкий физик
(1879— 
обратил внимание то, что кристаллы можно использовать в качестве пространственных решеток для наблюдения дифракции рентгенов- ского излучения, поскольку расстояние между атомами в кристаллах одного по- рядка с длиной волны рентгеновского излучения м).
Метод расчета дифракции рентгено- вского излучения от кристаллической решетки предложен независимо друг от друга русским ученым Г. В.Вульфом 
— 1925) и английскими физиками Г. и Л.Брэггами [отец (1862-1942) и сын (1890 
Они предположили, что дифракция рентгеновского излуче- ния является результатом его отраже- ния от системы параллельных кристал- лографических плоскостей (плоско- стей, в которых лежат узлы (атомы) кристаллической решетки).
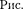Представим кристалл в виде сово- купности параллельных кристаллогра- фических плоскостей (рис. 267), отсто- ящих друг от друга на расстоянии d. Пу- чок параллельных монохроматических рентгеновских лучей (7, 2) падает под углом скольжения 0 (угол между на- правлением падающих лучей и крис- таллографической плоскостью) и воз- буждает атомы кристаллической ре- шетки, которые становятся источника- ми когерентных вторичных волн 1' 2', интерферирующих между собой, подоб- но вторичным волнам, от щелей диф- ракционной решетки. Максимумы ин-
 |
тенсивности (дифракционные макси- мумы) наблюдаются в тех направлени- ях, в которых все отраженные атомны- ми плоскостями волны будут находить- ся в одинаковой фазе. Эти направления удовлетворяют формуле Вульфа —
Брэггов
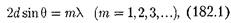
т. е. при разности хода между двумя лу- чами, отраженными от соседних крис- таллографических плоскостей, кратной целому числу длин волн X, наблюдает- ся дифракционный максимум.
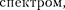При произвольном направлении па- дения монохроматического рентгено- вского излучения на кристалл дифрак- ция не возникает. Чтобы ее наблюдать, надо, поворачивая кристалл, найти угол скольжения. Дифракционная картина может быть получена и при произволь- ном положении кристалла, для чего нужно пользоваться непрерывным рен- тгеновским испускаемым рентгеновской трубкой. Тогда для та- ких условий опыта всегда найдутся дли- ны волн X, удовлетворяющие условию (182.1). -
Формула Вульфа — Брэггов исполь- зуется при решении двух важных за- дач:
1. 
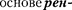Наблюдая дифракцию рентгено- вского излучения известной длины волны на кристаллической структуре неизвестного строения и измеряя 0 и т, можно найти межплоскостное рассто- яние (d), т.е. определить структуру ве- щества. Этот метод лежит в тгеноструктурногоанализа.
Формула Вульфа 
остает- ся справедливой и при дифракции элек- тронов и нейтронов. Методы исследо- вания структуры вещества, основанные дифракции электронов и нейтронов, называются соответственно электро-
нографией и нейтронографией.
2. Наблюдая дифракцию рентгено- вского излучения неизвестной длины волны на кристаллической
известном d измеряя мож- но найти длину волны падающего рен- тгеновского излучения. Этот метод ле- жит в рентгеновской спектро- скопии.
§ 183. Разрешающая способность оптических приборов
Используя даже идеальную оптиче- скую систему (такую, для которой от- сутствуют дефекты и аберрации), не- возможно получить стигматическое изображение точечного источника, что объясняется волновой природой света. Изображение любой светящейся точки в монохроматическом свете представ- ляет собой дифракционную картину, т. е. точечный источник отображается в виде центрального светлого пятна, ок- руженного чередующимися темными и светлыми кольцами.
Согласно критерию Рэлея, изобра- жения двух близлежащих одинаковых точечных источников или двух близле- жащих спектральных линий с равными
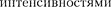и одинаковыми сим- метричными контурами разрешимы (разделены для восприятия), если цен- тральный максимум дифракционной картины от одного источника (линии)
Наши рекомендации |