Реальные газы, жидкости и твердые тела

§ 60. Силы и потенциальная энергия межмолекулярного взаимодействия

Модель идеального газа (см. § 41), ис- пользуемая в молекулярно-кинетиче- ской теории газов, позволяет довольно хорошо описывать поведение разрежен- ных реальных газов. При выводе урав- нения состояния идеального газа раз- мерами молекул и их взаимодействием друг с другом пренебрегают. Повыше- ние давления приводит к уменьшению среднего расстояния между молекула- ми, поэтому необходимо учитывать объем молекул и взаимодействие меж- ду ними. Так, в 1 м3 газа при нормаль- ных условиях содержится 2,68 • 1025мо- лекул, занимающих объем примерно 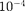м3 (радиус молекулы примерно 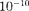м), которым по сравнению с объе- мом газа (1 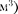можно пренебречь. При давлении 500 МПа (1 атм = 101,3 кПа)

объем молекул составит уже половину всего объема газа. Таким образом, при высоких давлениях указанная модель идеального газа

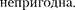При рассмотрении реальных га- зов — газов, свойства которых зависят от взаимодействия молекул, надо учи- тывать силы межмолекулярного вза- имодействия. Они проявляются на расстояниях 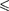10~9 м и быстро убыва- ют с увеличением расстояния между молекулами. Такие силы называются короткодействующими.

В XX в., по мере развития представ- лений о строении атома и квантовой ме- ханики, было выяснено, что между мо- лекулами вещества одновременно дей- ствуют силы притяжения и силы от- талкивания. На рис. 90, а приведена качественная зависимость сил межмо- лекулярного взаимодействия от расс- тояния между молекулами, где

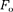
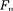— соответственно силы отталкива-

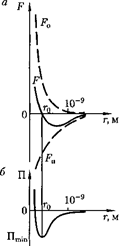Рис.90

ния и притяжения, a F — их результи- рующая.

Силы отталкивания считаются поло- жительными, а силы взаимного притя- жения — отрицательными.

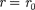
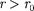На расстоянии результирую- щая сила F = 0, т. е. силы притяжения и отталкивания уравновешивают друг друга. Таким образом, расстояние со- ответствует равновесному расстоянию между молекулами, на котором бы они находились в отсутствие теплового дви- жения. При 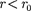преобладают силы от- талкивания (F > 0), при — силы притяжения (F < 0). На расстояниях

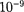> м межмолекулярные силы вза- имодействия практически отсутствуют

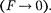
Элементарная работа 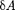силы 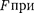увеличении расстояния между молеку- лами на r совершается за счет умень- шения взаимной потенциальной энер- гии молекул, т. е.

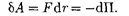(60.1)

Изанализа качественной зависимо- сти потенциальной энергии взаимодей- ствия молекул от расстояния между ними (рис. 90, б) следует, что если мо-

лекулы находятся друг от друга на рас- стоянии, на котором межмолекулярные силы взаимодействия не действуют 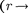сю), то П 0. При постепенном сближении молекул между ними появ- ляются силы притяжения (F < 0), ко- торые совершают положительную рабо- ту (ЬА = Fdr > 0). Тогда, согласно (60.1), потенциальная энергия взаимо- действия уменьшается, достигая мини- мума при

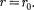
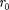
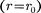При < с уменьшением силы от- талкивания (F > 0) резко возрастают и совершаемая против них работа отри- цательна (ЬА = 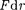< 0). Потенциаль- ная энергия начинает также резко воз- растать и становится положительной. Из данной потенциальной кривой сле- дует, что система из двух взаимодей- ствующих молекул в состоянии устой- чивого равновесия обладает ми- нимальной потенциальной энергией.

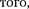Критерием различных агрегатных состояний вещества является соотно- шение между величинами 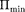и кТ. 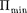— наименьшая потенциальная энергия взаимодействия молекул — оп- ределяет работу, которую нужно совер- шить против сил притяжения для чтобы разъединить молекулы, находя- щиеся в равновесии (г = 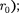кТ опре- деляет удвоенную среднюю энергию, приходящуюся на одну степень свобо- ды хаотического (теплового) движения молекул.

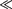
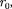Если 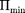кТ, то вещество нахо- дится в газообразном состоянии, так как интенсивное тепловое движение моле- кул препятствует соединению молекул, сблизившихся до расстояния т. е. ве- роятность образования агрегатов из мо- лекул достаточно мала.

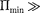Если кТ, то вещество находит- ся в твердом состоянии, так как молеку- лы, притягиваясь друг к другу, не могут удалиться на значительные расстояния

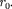и колеблются около положений равно- весия, определяемого расстоянием

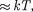
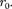Если 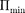то вещество нахо- дится в жидком состоянии, так как в ре- зультате теплового движения молеку- лы перемещаются в пространстве, об- мениваясь местами, но не расходясь на расстояние, превышающее

Таким образом, любое вещество в зависимости от температуры может на- ходиться в газообразном, жидком или твердом агрегатном состоянии, причем температура перехода из одного агре- гатного состояния в другое зависит от значения 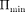для данного вещества. Например, у инертных газов 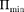мало, у металлов велико, поэтому при обыч- ных (комнатных) температурах они находятся соответственно в газообраз-

ном и твердом состояниях.

§ 61. Уравнение Ван-дер-Ваальса

Как указывалось в § 60, для реаль- ных газов необходимо учитывать раз- меры молекул и их взаимодействие друг с другом, поэтому модель идеаль- ного газа и уравнение Клапейрона — Менделеева (42.4) 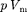= RT (для 1 моль газа), описывающее идеальный газ, для реальных газов непригодны.

Учитывая собственный объем моле- кул и силы межмолекулярного взаимо- действия, голландский физик И.Ван-

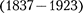вывел уравне- ние состояния реального газа. Ван-дер- Ваальсом в уравнение Клапейрона — Менделеева введены две поправки.

Учет собственного объема моле- кул.Наличие сил отталкивания, кото- рые противодействуют проникновению в занятый молекулой объем других мо- лекул, сводится к тому, что фактический свободный объем, в котором могут дви- гаться молекулы реального газа, будет

не 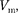a 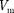- b, где Ь— объем, занимае- мый самими молекулами. Объем Ьравен учетверенномусобственномуобъемумо- лекул. Если, например, в сосуде находят- ся две молекулы, то центр любой из них не может приблизиться к центру другой молекулы на расстояние, меньшее диа- метра 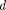молекулы. Это означает, что для центров обеих молекул оказывается не- доступным 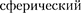объем радиу- са d, т. е. объем, равный восьми объемам молекулы или учетверенному объему молекулы в расчете на одну молекулу.

2. Учет притяжения молекул.Дей- ствие сил притяжения газа приводит к появлению дополнительного давления на газ, называемого внутренним дав- лением. По вычислениям Ван-дер-Ва- альса, внутреннее давление обратно пропорционально квадрату молярного объема:

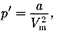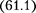где — постоянная Ван-дер-Ваальса, характеризующая силы межмолеку- лярного притяжения; 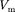— молярный объем.

Вводя эти поправки, получим урав- нение Ван-дер-Ваальса для 1 мольгаза

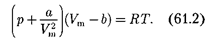{уравнение состояния реальных га- зов):

Для произвольного количества ве- щества v газа (у = 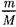) с учетом того,

чтоV—v 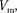уравнениеВан-дер-Вааль-

са примет вид

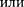
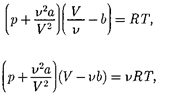
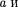где поправки Ъ — постоянные для каждого газа величины, определяемые опытным путем (записываются уравне- ния Ван-дер-Ваальса для двух извест- ных из опыта состояний газа и решают- ся относительно а и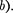

При выводе уравнения Ван-дер-Ва- альса сделан целый ряд упрощений, поэтому оно также весьма приближен- ное, хотя и лучше (особенно для не- сильно сжатых газов) согласуется с опытом, чем уравнение состояния иде- ального газа.

§62.Изотермы Ван-дер-Ваальса и их анализ

Для исследования поведения реаль- ного газа рассмотрим изотермы Ван- дер-Ваальса — кривые зависимости р от 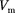при заданных Т, определяемые уравнением Ван-дер-Ваальса (61.2) для 1 моль газа. Эти кривые (рассматрива- ются для четырех различных темпера- тур; рис. 91) имеют довольно своеобраз- ный характер. При высоких температу- рах (Т > 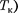изотерма реального газа отличается от изотермы идеального газа только некоторым искажением ее формы, оставаясь монотонно спадаю- щей кривой. При некоторой температу- ре 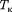на изотерме имеется лишь одна точка перегиба К. Эта изотерма назы- вается критической, соответствующая

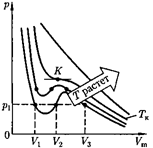Рис.91

ей температура 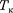— критической температурой;точка перегиба 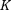на- зывается критической точкой; в этой точке касательная к ней параллельна оси абсцисс. Соответствующие этой точке объем 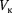и давление называ- ются также критическими.

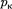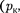
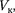
Состояние с критическими парамет- рами 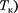называется критиче- ским состоянием. При низких темпе- ратурах ( Т < 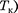изотермы имеют вол- нообразный участок, сначала монотон- но опускаясь вниз, затем монотонно поднимаясь вверх и снова монотонно опускаясь.

Для пояснения характера изотерм преобразуем уравнение Ван-дер-Вааль- са (61.2) к виду

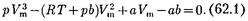
Уравнение (62.1) при заданных р и Т является уравнением третьей степе- ни относительно 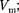следовательно, оно может иметь либо три веществен- ных корня, либо один вещественный и два мнимых, причем физический смысл имеют лишь вещественные положи- тельные корни. Поэтому первому слу- чаю соответствуют изотермы при низ- ких температурах (три значения объема газа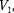 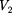и 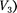отвечают (индекс «т» для простоты опускаем) одному значе- нию давления 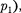второму случаю — изотермы при высоких температурах.

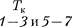Рассматривая различные участки изотермы при Т < (рис. 92), видим, что на участках при умень- шении объема 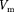давление р растет, что естественно. На участке 3 — 5 сжатие ве- щества приводит к уменьшению давле- ния; практика же показывает, что такие состояния в природе не осуществляют- ся. Наличие участка 3 — 5 означает, что при постепенном изменении объема вещество не может оставаться все вре- мя в виде однородной среды; в некото-

рыи момент должно наступить скачко- образное изменение состояния и распад вещества на две фазы. Таким образом, истинная изотерма будет иметь вид ло- маной линии 7—6 — 2—1.

Часть 6—7 отвечает газообразному состоянию, а часть 2—1 — жидкому. В состояниях, соответствующих гори- зонтальному участку изотермы 6 — 2, наблюдается равновесие жидкой и га- зообразной фаз вещества. Вещество в газообразном состоянии при темпера- туре ниже критической называется па- ром, а пар, находящийся в равновесии со своей жидкостью, называется насы- щенным.

Данные выводы, следующие из ана- лиза уравнения Ван-дер-Ваальса, были подтверждены опытами ирландского ученого Т. Эндрюса (1813— 1885), изу- чавшего изотермическое сжатие угле- кислого газа. Отличие эксперимен- тальных (Эндрюс) и теоретических (Ван-дер-Ваальс) изотерм заключается в том, что превращению газа в жидкость в первом случае соответствуют гори- зонтальные участки, а во втором — вол- нообразные.

Для нахождения критических пара- метров подставим их значения в урав- нение (62.1) и запишем

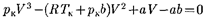(62.2)

(индекс «т» для простоты опускаем). Поскольку в критической точке все три корнясовпадаютиравны 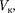уравнение приводится к виду

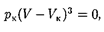
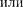
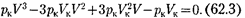
Так как уравнения (62.2) и (62.3) тождественны, то в них должны быть равны и коэффициенты при

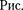92

ных соответствующих степеней. Поэто- му можно записать

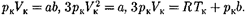Решая полученные уравнения, най- дем

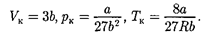(62.4)

Если через крайние точки горизон- тальных участков семейства изотерм (см. рис. 92) провести линию, то полу- чится колоколообразная кривая (рис. 93), ограничивающая область двухфаз- ных состояний вещества. Эта кривая и критическая изотерма делят диаграмму р, 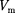под изотермой натри области: под колоколообразной кривой располагает- ся область двухфазных состояний (жидкость и насыщенный пар), слева от нее находится область жидкого состоя- ния, а справа — область пара.

Пар отличается от остальных газо- образных состояний тем, что при изо- термическом сжатии претерпевает про- цесс сжижения. Газ же при температу- ре выше критической не может быть превращен в жидкость ни при каком давлении.

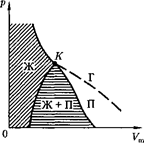Рис. 93

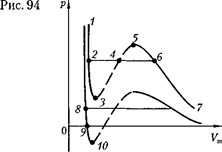
Сравнивая изотерму Ван-дер-Вааль- са с изотермой Эндрюса (верхняя кри- вая на рис. 94), видим, что последняя имеет прямолинейный участок 2 — 6, соответствующий двухфазным состоя- ниям вещества. Правда, при некоторых условиях могут быть реализованы со- стояния, изображаемые участками ван- дер-ваальсовой изотермы 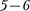и 2—3. Эти неустойчивые состояния называ- ются метастабилъными. Участок 2—3 изображает перегретую жидкость, 5—6 — пересыщенный пар. Обе фазы ограниченно устойчивы.

При достаточно низких температу- рах изотерма пересекает ось 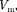пере- ходя в область отрицательных давле- ний (нижняя кривая на рис. 94). Веще- ство под отрицательным давлением на- ходится в состоянии растяжения. При некоторых условиях такие состояния также реализуются. Участок 8 — 9 на нижней изотерме соответствует пере- гретой жидкости, участок 9—10 — растянутой жидкости.

§63. Внутренняя энергия реального газа

Внутренняя энергия реального газа складывается из кинетической энергии теплового движения его молекул (оп- ределяет внутреннюю энергию идеаль- ного газа, равную 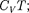см. § 53) и по-

энергии межмолекуляр- ного взаимодействия. Потенциальная энергия реального газа обусловлена только силами притяжения между мо- лекулами. Наличие сил притяжения приводит квозникновению внутренне- го давления на газ [см. (61.1)]:

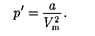Работа, которая затрачивается для преодоления сил притяжения, действу- ющих между молекулами газа, как из- вестно из механики, идет на увеличение потенциальной энергии системы, т.е.

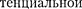
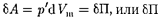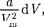= от-

куда

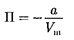(постоянная интегрирования принята равной нулю). Знак «—» означает, что молекулярные силы, создающие внут- реннее давление 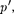являются силами притяжения (см. § 60). Учитывая оба слагаемых, получим, что внутренняя энергия 1 моль реального газа

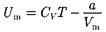(63.1)

растет с повышением температуры и увеличением объема.

Если газ расширяется без теплооб- мена с окружающей средой (адиабат- ный процесс, т. е. 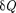= 0) и не соверша- ет внешней работы (расширение газа в вакуум, т.е. ЬА — 0), то на основании первого начала термодинамики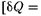

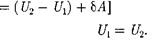получим, что

(63.2)

Следовательно, при адиабатном рас- ширении без совершения внешней ра- боты внутренняя энергия газа не изме- няется.

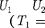Равенство (63.2) формально спра- ведливо как для идеального, так и для реального газов, но его физический смысл для обоих случаев совершенно различен. Для идеального газа равен- ство — означаетравенство темпе- ратур 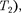т.е. при адиабатном расширении идеального газа в вакуум его температура не изменяется. Для ре- ального газа из равенства (63.2), учиты- вая, что для 1 моль газа

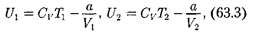получим

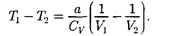
Так как 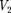> 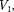то 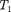> 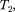т.е. ре- альный газ при адиабатном расшире- нии в вакуум охлаждается. При адиа- батном сжатии в вакуум реальный газ нагревается.

§64.ЭффектДжоуля—Томсона

Если идеальный газ адиабатно рас- ширяется и совершает при этом рабо- ту, то он охлаждается, так как работа в данном случае совершается за счет его внутренней энергии (см. § 55). Подоб- ный процесс, но с реальным газом — адиабатное расширение реального газа с совершением внешними силами поло- жительной работы — осуществили анг- лийские физики Джоуль (1818— 1889) и (лорд Кельвин, 1824-1907).

Рассмотрим эффект Джоуля — Том- сона. На рис. 95 представлена схема их опыта. В теплоизолированной трубке с пористой перегородкой находятся два поршня, которые могут перемещаться без трения. Пусть сначала слева от пе-

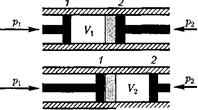Рис.95 регородки газ под поршнем 1

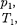
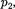ся под давлением занимает объем при температуре а справа газ отсут- ствует (поршень 2 придвинут к перего- родке). После прохождения газа через пористую перегородку в правой части газ характеризуется параметрами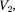

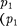
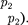
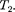Давления и поддерживаются

>

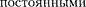Так как расширение газа происходит без теплообмена с окружающей средой (адиабатно), то на основании первого начала термодинамики

(64.1)

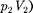
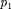Внешняя работа, совершаемая газом, состоит из положительной работы при движении поршня 2 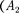— и от- рицательной при движении поршня 1 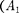= 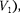т.е. 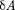= 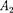- 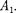Подстав- ляя выражения для работ в формулу (64. 1), получим

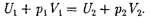(64.2)

Таким образом, в опыте Джоуля — Томсона сохраняется (остается неиз- менной) величина 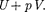Она являет- ся функцией состояния и называется энтальпией.

Ради простоты рассмотрим 1 моль газа. Подставляя в формулу (64.2) вы- ражение (63.3) и рассчитанные из урав- нения Ван-дер-Ваальса (61.2) значения

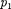
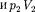
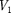(индекс «т» опять опуска- ем) и производя элементарные преоб- разования, получаем

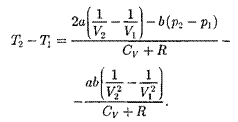(64.3)

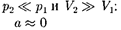Извыражения (64.3) следует, что знакразности ( 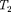— 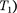зависит от того, какая из поправок Ван-дер-Ваальса иг- рает большую роль. Проанализируем данное выражение, сделав допущение, что

1) —не учитываем силы при- тяжения между молекулами, аучитыва- ем лишь размеры самих молекул. Тогда

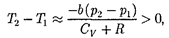
т.е. газ в данном случае нагревается;

2) Ь 0 — неучитываемразмеров мо- лекул, а учитываем лишь силы притя- жения между молекулами. Тогда

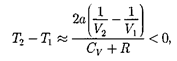
т. е. газ в данном случае охлаждается;

3) 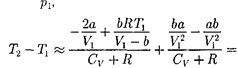учитываем обе поправки. Подста- вив в выражение (64.3) вычисленное из уравнения Ван-дер-Ваальса (61.2) зна- чение имеем

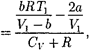(64.4)

т. е. знак разности температур зависит от значений начального объема 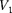и начальной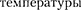

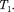
Изменение температуры реального газа врезультате его адиабатного рас-

ширения, или, как говорят, адиабат- ного дросселирования — медленного прохождения газа под действием пере- пада давления сквозь дроссель(напри- мер, пористую перегородку), называет- ся эффектомДжоуля— Томсона. Эф- фект Джоуля — Томсона принято назы- вать положительным, если газ в про- цессе дросселирования охлаждается 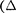Т < 0), и отрицательным, если газ нагревается 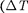> 0).

В зависимости от условий дроссели- рования для одного и того же газа эф- фект Джоуля —Томсона может быть как положительным, так и отрицатель- ным. Температура, при которой (для данного давления) происходит измене- ние знака эффекта Джоуля —Томсона, называется температурой инверсии. Ее зависимость от объема получим, приравняв выражение (64.4) нулю:

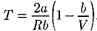(64.5)

Кривая, определяемая уравнением (64.5), — кривая инверсии — приведе- на на рис. 96. Область выше этой кри- вой соответствует отрицательному эф- фекту Джоуля —Томсона, ниже — по- ложительному. Отметим, что при боль- ших перепадах давления на дросселе температура газа изменяется значи- тельно. Так, при дросселировании от 20 до 0,1 МПа и начальной температуре 17 °С воздух охлаждается на 35 °С.

Эффект Джоуля —Томсона обус- ловлен отклонением газа от идеалыю-

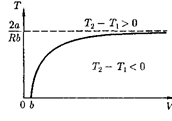Рис. 96

сти. В самом деле, для 1 моль идеаль- ного газа р 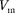= RT, поэтому выраже- ние (64.2) примет вид

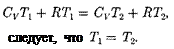откуда

§ 65. Сжижение газов

Рис. 97

нике (X) до температуры ниже темпе-

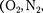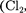
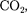
Превращение любого газа в жид- кость — сжижение газа — возможно лишь при температуре ниже критиче- ской (см. § 62). При ранних попытках сжижения газов оказалось, что некото- рые газы 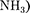легко сжижа- лись изотермическим сжатием, а целый ряд газов 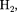Не) сжижению не поддавался. Подобные неудачные по- пытки объяснил Д. И. Менделеев, пока- зав, что сжижение этих газов произво- дилось при температуре, большей кри- тической, и поэтому заранее было об- речено на неудачу. Впоследствии уда- лось получить жидкие кислород, азот и водород (их критические температуры равны соответственно 154,4, 126,1 и 33 К), а в 1908 г. нидерландский физик

(1853—1926) до-

бился сжижения гелия, имеющего са- мую низкую критическую температуру (5,3 К).

Для сжижения газов чаще применя- ются два промышленных метода, в ос- нове которых используется либо эф- фект Джоуля Томсона, либо охлажде- ние газа при совершении им работы.

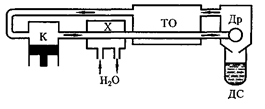
Схема одной из установок, в которой используется эффект Джоуля — Томсо- на, — машины — представлена на рис. 97. Воздух в компрессоре (К) сжимается до давления в десятки ме- гапаскалей и охлаждается в холодиль-

К.Линде (1842—1934) — немецкий физик и инженер.

ратуры инверсии, в результате чего при дальнейшем расширении газа наблюда- ется положительный эффект Джоуля — Томсона (охлаждение газа при его рас- ширении). Затем сжатый воздух прохо- дит по внутренней трубе теплообмен- ника (ТО) и пропускается через дрос- сель (Др), при этом он сильно расши- ряется и охлаждается. Расширивший- ся воздух вновь засасывается по внеш- ней трубе теплообменника, охлаждая вторую порцию сжатого воздуха, теку- щего по внутренней трубе.

Так как каждая следующая порция воздуха предварительно охлаждается, а затем пропускается через дроссель, то температура понижается все больше. В результате 6— 8-часового цикла часть воздуха 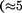%), охлаждаясь до темпе- ратуры ниже критической, сжижается и поступает в дьюаровский сосуд (ДС) (см. § 49), а остальная его часть возвра- щается в теплообменник.

Второй метод сжижения газов осно- ван на охлаждении газа при соверше- нии им работы. Сжатый газ, поступая в поршневую машину (детандер), рас- ширяется и совершает при этом работу по передвижению поршня. Так как ра- бота совершается за счет внутренней энергии газа, то его температура при этом понижается.

Академик П.Л.Капица предложил вместо детандера применять турбоде- тандер, в котором газ, сжатый всего лишь до 500 — 600 кПа, охлаждается,

совершает работу по вращению турби- ны. Этот метод успешно применен Ка- пицей для сжижения гелия, предвари- тельное охлаждение которого произво- дилось жидким азотом. Современные мощные холодильные установки рабо- тают по принципу турбодетандера.

§ 66. Свойства жидкостей. Поверхностное натяжение

Жидкость является агрегатным со- стоянием вещества, промежуточным между газообразным и твердым, поэто- му она обладает свойствами как газооб- разных, так и твердых веществ. Жидко- сти, подобно твердым телам, имеют оп- ределенный объем, а подобно газам, принимают форму сосуда, в котором они находятся (см. § 28). Молекулы газа практически не связаны между со- бой силами межмолекулярного взаимо- действия, и в данном случае средняя энергия теплового движения молекул газа гораздо больше средней потенци- альной энергии, обусловленной силами притяжения между ними (см. § 60), по- этому молекулы газа разлетаются в раз- ные стороны и газ занимает предостав- ленный ему объем.

В твердых и жидких телах силы при- тяжения между молекулами уже суще- ственны и удерживают молекулы на оп- ределенном расстоянии друг от друга. В этом случае средняя энергия хаоти- ческого (теплового) движения молекул меньше средней потенциальной энер- гии, обусловленной силами межмоле- кулярного взаимодействия, и ее недо- статочно для преодоления сил притя- жения между молекулами, поэтому твердые тела и жидкости имеют опре- деленный объем.

Рентгеноструктурный анализ жид- костей показал, что характер располо-

жения частиц жидкости промежуточен между газом и твердым телом. В газах молекулы движутся хаотично, поэтому нет никакой закономерности в их вза- имном расположении. Для твердых тел наблюдается так называемый дальний порядок в расположении частиц, т. е. их упорядоченное расположение, повторя- ющееся на больших расстояниях. В жид- костях имеет место так называемый ближнийпорядок врасположении ча- стиц, т. е. их упорядоченное расположе- ние, повторяющееся на расстояниях, сравнимых с межатомными.

Теория жидкости до настоящего вре- мени полностью не развита. Разработка ряда проблем в исследовании свойств жидкости принадлежит Я. И. Френке- лю (1894 — 1952). Тепловое движение в жидкости он объяснял тем, что каждая молекула в течение некоторого време- ни колеблется около определенного положения равновесия, после чего скачком переходит в новое положение, отстоящее от исходного на расстоянии порядка межатомного. Таким молекулы жидкости довольно медлен- но перемещаются по всей массе жидко- сти и диффузия происходит гораздо медленнее, чем в газах. С повышением температуры жидкости частота колеба- тельного движения резко увеличивает- ся, возрастает подвижность молекул, что, в свою очередь, является причиной уменьшения вязкости жидкости.

На каждую молекулу жидкости со стороны окружающих молекул дей- ствуют силы притяжения, быстро убы- вающие с расстоянием (см. рис. 90); следовательно, начиная с некоторого минимального расстояния силами при- тяжения между молекулами можно пренебречь. Это расстояние (порядка 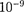м) называется радиусом молеку- лярного действия а сфера радиуса г — сферой молекулярного действия.

Выделим внутри жидкости какую- либо молекулу А (рис. 98) и проведем вокруг нее сферу радиусом Достаточ- но, согласно определению, учесть дей- ствие на данную молекулу только тех молекул, которые находятся внутри сферы молекулярного действия. Силы, с которыми эти молекулы действуют на молекулу А, направлены в разные сто- роны и в среднем скомпенсированы, поэтому результирующая сила, дей- ствующая на молекулу внутри жидко- сти со стороны других молекул, равна нулю.

Иначе обстоит дело, если молекула, например молекула В, расположена от поверхности на расстоянии, мень- шем В данном случае сфера молеку- лярного действия лишь частично рас- положена внутри жидкости. Так как концентрация молекул в расположен- ном над жидкостью газе мала по срав- нению с их концентрацией в жидкости, то равнодействующая сил F, прило- женных к каждой молекуле поверхно- стного слоя, не равна нулю и направ- лена внутрь жидкости. Таким образом, результирующие силы всех молекул поверхностного слоя оказывают на жидкость давление, называемое моле- кулярным (или внутренним). Моле- кулярное давление не действует на тело, помещенное в жидкость, так как оно обусловлено силами, действующи- ми только между молекулами самой

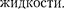
Суммарная энергия частиц жидко- сти складывается из энергии их хаоти- ческого (теплового) движения и потен- циальной энергии, обусловленной си- лами межмолекулярного взаимодей- ствия. Для перемещения молекулы из глубины жидкости в поверхностный слой надо затратить работу. Эта работа совершается за счет кинетической энер- гии молекул и идет на увеличение их

Рис. 98

потенциальной энергии. Поэтому моле- кулы поверхностного слоя жидкости обладают большей потенциальной энергией, чем молекулы внутри жидко- сти. Эта дополнительная энергия, кото- рой обладают молекулы в поверхност- ном слое жидкости, называемая поверх- ностной энергией, пропорциональна площади слоя AS:

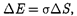(66.1)

где ст— поверхностное натяжение.

Так как равновесное состояние ха- рактеризуется минимумом потенциаль- ной энергии, то жидкость при отсут- ствии внешних сил будет принимать такую форму, чтобы при заданном объеме она имела минимальную повер- хность, т.е. форму шара. Наблюдая мельчайшие капельки, взвешенные в воздухе, можем видеть, что они дей- ствительно имеют форму шариков, но несколько искаженную из-за действия сил земного тяготения. В условиях не- весомости капля любой жидкости (не- зависимо от ее размеров) имеет сфери- ческую форму, что доказано экспери- ментал