Цикл Карно и его КПД для идеального газа

Из формулировки второго начала термодинамики по Кельвину следует, что вечный двигатель второгорода — периодически действующий двигатель, совершающий работу за счет охлажде- ния одного источника теплоты, — не- возможен. Для иллюстрации этого по- ложения рассмотрим работу теплового двигателя (исторически второе начало термодинамики и возникло из анализа работы тепловых двигателей).

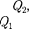Принцип действия теплового двига- теля приведен на рис. 87. От термоста- та1с более высокой температурой 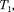на- зываемого нагревателем, за цикл отби- рается количество теплоты 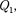а термо- стату с более низкой температурой 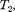называемому холодильником, за цикл передается количество теплоты при этом совершается работа А = —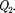

Чтобы термический коэффициент полезного действия теплового двигате- ля (56.2) был равен 1, необходимо вы- полнение условия 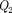= 0, т. е. тепловой двигатель должен был бы иметь один

1 Термодинамическая система, которая мо- жет обмениваться теплотой с телами без изме- нения температуры.

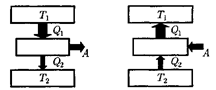
Рис.87 Рис. 88

источник теплоты. Однако, согласно Карно1, для работы теплового двигате- ля необходимо не менее двух источни- ков теплоты с различными температу- рами, иначе это противоречило бы вто- рому началу термодинамики.

Двигатель второго рода, будь он возмо- жен, был бы практически вечным. Охлаж- дение, например, воды океанов на 1° дало бы огромную энергию. Масса воды в Мировом океане составляет примерно 1018т, при ох- лаждении которой на 1° выделилось бы при- мерно 1024Дж теплоты, что эквивалентно полному сжиганию 1014т угля. Железнодо- рожный состав, нагруженный таким коли- чеством угля, растянулся бы на расстояние 1010км, что приблизительно совпадает с раз- мерами Солнечной системы!

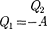
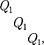Процесс, обратный происходящему в тепловом двигателе, используется в холодильной машине, принцип дей- ствия которой представлен на рис. 88. Системой за цикл от термостата с бо- лее низкой температурой 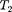отбирает- ся количество теплоты 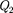и отдается за цикл термостату с более высокой тем- пературой 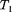количество теплоты 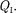Для кругового процесса, согласно (56.1), 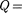А, но, по условию, Q = — < О, поэтому А < 0 и 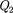— или =

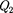+ А, т.е. количество теплоты отданное системой источнику теплоты при более высокой температуре 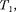больше количества теплоты 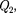полу- ченного от источника теплоты при бо- лее низкой температуре 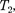на величи-

1 Н. Л. С. Карно (1796-1832) - французский физик и инженер.

ну работы, совершенной над системой. Следовательно,безсовершенияработы нельзя отбирать теплоту отменее на- гретоготелаиотдаватьееболеенагре- тому. Это утверждение есть не что иное, как второе начало термодинами- ки в формулировке Клаузиуса.

Однако второе начало термодинами- ки не следует представлять так, что оно совсем запрещает переход теплоты от менее нагретого тела к более нагрето- му. Ведь именно такой переход осуще- ствляется в холодильной машине. Но при этом надо помнить, что внешние силы совершают работу над системой, т. е. этот переход не является единствен- ным результатом процесса.

Из всех периодически действующих тепловых машин, имеющих одинако- вые температуры нагревателей 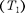и холодильников ( 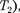наибольшим КПД обладают обратимые машины; при этом КПД обратимых машин, работающих при одинаковых температурах нагрева- телей 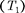и холодильников 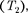рав- ны друг другу и не зависят от природы рабочего тела (тела, совершающего кру- говой процесс и обменивающегося энергией с другими телами), а опреде- ляются только температурами нагрева- теля и холодильника. Это утверждение носит название теоремы Карно.

Из всевозможных круговых процес- сов важное значение в термодинамике имеет цикл Карно — цикл, состоящий из четырех последовательных обрати- мых процессов: изотермического рас- ширения, адиабатного расширения, изотермического сжатия и адиабатно- го сжатия.

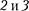Прямой цикл Карно изображен на рис. 89, где изотермические расширение и сжатие заданы соответственно кривы- ми 1 — — 4, а адиабатные расшире- ние и сжатие — кривыми 2—3 и 4—1. При изотермическом процессе U— const,

поэтому, согласно (54.4), количество теплоты 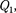полученное газом от нагре- вателя, равно работе расширения 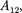совершаемой газом при переходе из со- стояния 1 в состояние 2:

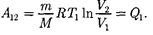(59.1)

При адиабатном расширении 2—3 теплообмен с окружающей средой от- сутствует и работа расширения 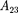со- вершается засчет изменения внутрен- ней энергии [см. (55.1) и (55.8)]:

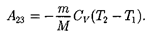Количество теплоты 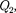отданное га- зом холодильнику при изотермическом сжатии, равно работе сжатия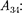

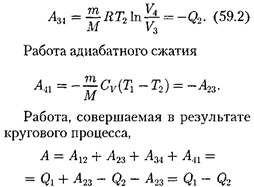
и определяется площадью, тонирован- ной нарис. 89.

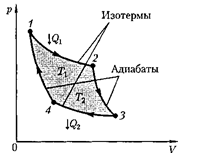Рис. 89

Термический КПДцикла Карно, со- гласно (56.2),

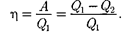
Применив уравнение (55.5) для ади- абат 2 — 3 и 4—1, получим

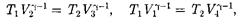
откуда

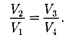(59.3)

Подставляя (59.1) и (59.2) в форму-

лу (56.2) и учитывая (59.3), получаем

Обратный цикл Карно положен в основу действия тепловых насосов. Вотличие от холодильных машин теп- ловые насосы должны как можно боль- ше тепловой энергии отдавать горяче- му телу, например системе отопления. Часть этой энергии отбирается от окру- жающей среды с более низкой темпера- турой, ачасть получается засчет меха- нической работы, производимой, на- пример,компрессором.

Теорема Карно послужила основа- нием для установления термодинами- ческой шкалы температур. Сравнив левую и правую части формулы (59.4), получим

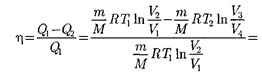
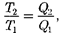(59.5)

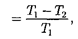(59.4)

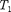т. е. для цикла Карно КПД действитель- но определяется только температурами нагревателя и холодильника (доказа- тельство теоремы Карно). Для повыше- ния КПД необходимо увеличивать раз- ность температур нагревателя холо- дильника. Например, при = 400 К и 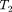= 300 К — 0,25. Если же темпера- туру нагревателя повысить на 100 К, а температуру холодильника понизить на 50 К, то = 0,5. КПД всякого реаль- ного теплового двигателя из-за трения и неизбежных тепловых потерь гораз- до меньше вычисленного для цикла Карно.

т.е. для сравнения температур 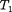и 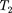двух тел необходимо осуществить цикл Карно, вкотором одно тело использу- ется вкачестве нагревателя, другое —как холодильник. Изравенства (59.5) видно, что отношение температур тел равно отношению отданного вэтом цикле количества теплоты кполучен- ному. Согласно теореме Карно, хими- ческий состав рабочего тела не влияет на результаты сравнения температур, поэтому такая термодинамическая шка- ла не связана со свойствами какого-то определенного термометрического тела. Отметим, что практически таким образом сравнивать температуры труд- но, так как реальные термодинамиче- ские процессы, как уже указывалось, являются необратимыми.

Контрольные вопросы

В чем суть закона Больцмана о равнораспределении энергии по степеням свободы моле- кул?

Почему колебательная степень свободы обладает вдвое большей энергией, чем поступа- тельная и вращательная?

Что такое внутренняя энергия идеального газа? В результате каких процессов может изменяться внутренняя энергия системы?

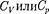• Что такое теплоемкость газа? Какая из теплоемкостей — — больше и почему?

• Как объяснить температурную зависимость молярной теплоемкости водорода?

• Чему равна работа изобарного расширения 1 моль идеального газа при нагревании на 1 К?

• Нагревается или охлаждается идеальный газ, если он расширяется при постоянном дав- лении?

• Температура газа в цилиндре постоянна. Запишите на основе первого начала термоди- намики соотношение между сообщенным количеством теплоты и совершенной рабо- той.

• Газ переходит из одного и того же начального состояния 1 в одно и то же конечное состо- яние 2 в результате следующих процессов: а) изотермического; б) изобарного; в) изо- хорного. Рассмотрев эти процессы графически, покажите: 1) в каком процессе работа расширения максимальна; 2) когда газу сообщается максимальное количество теп- лоты.

• Газ переходит из одного и того же начального состояния 1 в одно и то же конечное состо- яние 2 в результате следующих процессов: а) изобарного процесса; б) последователь- ных изохорного и изотермического процессов. Рассмотрите эти переходы графически. Одинаковы или различны в обоих случаях: 1) изменение внутренней энергии; 2) затра- ченное количество теплоты?

• Почему адиабата более крутая, чем изотерма?

• Как изменится температура газа при его адиабатном сжатии?

• Показатель политропы п > 1. Нагревается или охлаждается идеальный газ при сжатии?

• Проанализируйте прямой и обратный циклы.

• Чем отличаются обратимые и необратимые процессы? Почему все реальные процессы необратимы?

• Возможен ли процесс, при котором теплота, взятая от нагревателя, полностью преобра- зуется в работу?

• В каком направлении может изменяться энтропия замкнутой системы? незамкнутой системы?

• Дайте понятие энтропии (определение, размерность и математическое выражение энт- ропии для различных процессов).

• Изобразите в системе координат Т, S изотермический и адиабатный процессы.

• Представив цикл Карно на диаграмме р, 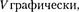укажите, какой площадью опре- деляется: 1) работа, совершенная над газам; 2) работа, совершенная самим расширяю- щимся газом.

• Представьте графически цикл Карно в переменных Т, S.

ЗАДАЧИ

9.1. Азот массой 1 кг находится при температуре 280 К. Определите: 1) внутреннюю энер- гию молекул азота; 2) среднюю кинетическую энергию вращательного движения молекул азота. Газ считать идеальным. [1) 208 кДж; 2) 83,1 кДж]

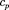
9.2. 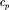Определите удельные теплоемкости и некоторого двухатомного газа, если плот- ность этого газа при нормальных условиях кг/м3. 650Дж/(кг • К), = 910 Дж/кг • К)]

9.3. 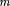Водород массой = 20 г был нагрет на 100 К при постоянном давлении. Опре- делите: 1) количество теплоты Q, переданное газу; 2) приращение 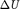внутренней энергии газа; 3) работу А расширения. [1) 29,3 кДж; 2) 20,9 кДж; 3) 8,4 кДж]

9.4. Кислород объемом 2 л находится под давлением 1 МПа. Определите, какое количе- ство теплоты необходимо сообщить газу, чтобы увеличить его давление вдвое в результате изохорного процесса. [5 кДж]

9.5. Некоторый газ массой 2 кг находится при температуре 300 К и под давлением 0,5 МПа. В результате изотермического сжатия давление газа увеличилось в три раза. Ра-

бота, затраченная па сжатие, А = -1,37 кДж. Определите: 1) какой это газ; 2) первоначаль- ный удельный объем газа. [1) гелий; 2) 1,25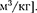

9.6. Двухатомный идеальный газ занимает объем 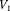1 л и находится под давлением

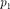
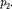— 0,1 МПа. После адиабатного сжатия газ характеризуется объемом 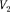и давлением

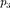
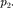В результате последующего изохорного процесса газ охлаждается до первоначальной тем- пературы, а его давление = 0,2 МПа. Определите: 1) объем 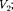2) давление Представь- те эти процессы графически. [1) 0,5 л; 2) 0,26 МПа]

9.7. Идеальный газ количеством вещества v — 2 моль сначала изобарно нагрели так, что его объем увеличился в п — 2 раза, а затем изохорно охладили так, что давление газа уменьшилось в п = 2 раза. Определите приращение энтропии в ходе указанных процессов. 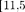Дж/К]

9.8.Тепловая машина, совершая обратный цикл Карно, за один цикл совершает работу 1 кДж. Температура нагревателя 400 К, а холодильника 300 К. Определите: 1) КПД маши- ны; 2) количество теплоты, получаемое машиной от нагревателя за цикл; 3) количество теплоты, отдаваемое холодильнику за цикл. [1) 25 %; 2) 4 кДж; 3) 3 кДж]

9.9. 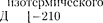Идеальный газ совершает цикл Карно, термический КПД которого равен 0,3. Опре- делите работу сжатия газа, если работа изотермического расширения со- ставляет 300 ж. Дж|

Глава 10