Механический принцип относительности

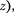Рассмотрим две системы отсчета: инерциальную систему К (с координа- тами х, у, которую условно будем считать неподвижной, и систему К' (с координатами х', у', 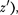движущую- ся относительно К равномерно и пря- молинейно со скоростью 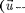const). Отсчет времени начнем с момента, ког-

да начала координат обеих систем со- впадают. Пусть впроизвольный момент времени t расположение этих систем относительно друг друга имеет вид, изображенный на рис. 60.Скорость направлена вдоль 00', радиус-вектор, проведенный из 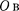О', —

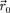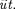
Найдем связь между координатами произвольной точки А в обеих систе- мах. Изрис. 60видно, что

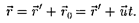(34.1)

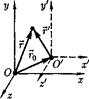Рис. 60

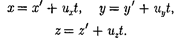Уравнение (34.1) можно записать в проекциях на оси координат:

(34.2)

Уравнения (34.1) и (34.2) носят на- звание преобразований координат Га- лилея.

В частном случае, когда система К' движется со скоростью v вдоль положи- тельного направления оси х системы К (в начальный момент времени оси ко- ординат совпадают), преобразования координат Галилея имеют вид

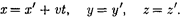
В классической механике предпола- гается, что ход времени не зависит от относительного движения систем от- счета, т.е. к преобразованиям (34.2) можно добавить еще одно уравнение:

t=t'. (34.3)

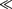Записанные соотношения справед- ливы лишь в случае классической меха- ники (и с), а при скоростях, сравни- мых со скоростью света, преобразования Галилея заменяются более общими пре- образованиями Лоренца1 (см. § 36).

Продифференцировав выражение (34.1) по времени [с учетом (34.3)], по- лучим уравнение

Ускорение всистеме отсчета К

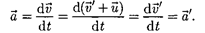
Таким образом, ускорение точки А в системах отсчета К К', движущихся относительно друг друга равномерно и прямолинейно, одинаково:

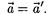(34.5)

Следовательно, если на точку А дру- гие тела не действуют (а =0), то, со- гласно (34.5), и 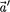= 0, т.е. система К' является инерциальной (точка движет- ся относительно нее равномерно и пря- молинейно или покоится).

Изуравнения (34.5) следует, что если выполняется равенство F — та, то выполняется и равенство F' = то! (мас- са имеет одинаковое числовое значение во всех системах отсчета). Поскольку системы К и К' были выбраны произ- вольно, то полученный результат озна- чает, что уравнения динамики при пере- ходе от одной инерциальной системы отсчета кдругой формулируются оди- наково. Это утверждение и есть меха- нический принцип относительности (принцип относительности Гали- лея). Галилей первым обратил внима- ние на то, что никакими механически- ми опытами, проведенными в данной инерциальной системе отсчета, нельзя установить, покоится ли она или дви- жется равномерно и прямолинейно. Например, сидя в каюте корабля, дви- жущегося равномерно и прямолинейно, мы не можем определить, покоится ко- рабль или движется, не выглянув в окно.

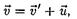(34.4)

которое представляет собой правило сложения скоростей в классической механике.

Х.Лоренц (1853—1928) — нидерландский физик-теоретик.

§ 35. Постулаты специальной (частной) теории относительности

Классическая механика Ньютона прекрасно описывает движение макро- тел, движущихся с малыми скоростями

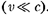Однако в конце XIX в. выясни- лось, что выводы классической механи- ки противоречат некоторым опытным данным, в частности при изучении дви- жения быстрых заряженных частиц оказалось, что их движение не подчи- няется законам классической механи- ки. Далее возникли затруднения при попытках применить механику Ньюто- на к объяснению распространения све- та. Если источник и приемник света движутся друг относительно друга рав- номерно и прямолинейно, то, согласно классической механике, измеренная скорость должна зависеть от относи- тельной скорости их движения.

Американский физик А. Майкель- сон (1852-1913) в 1881 г., а затем в 1887 г. совместно с Е.Морли (амери- канский физик, 1838—1923) пытался обнаружить движение Земли относи- тельно эфира (эфирный ветер) — опыт Майкельсона — Морли, применяя ин- терферометр, названный впоследствии интерферометром Майкельсона (см.

§ 175). Обнаружить эфирный ветер Майкельсону не удалось, как, впрочем, не удалось его обнаружить и в других многочисленных опытах. Опыты «уп- рямо» показывали, что скорости света в двух движущихся относительно друг друга системах равны. Это противо- речило правилу сложения скоростей классической механики.

Одновременно было показано проти- воречие между классической теорией и уравнениями (см. § 139) Дж. К. Макс- велла (английский физик, 1831 —1879), лежащими в основе понимания света как электромагнитной волны.

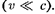Для объяснения этих и некоторых других опытных данных необходимо было создать новую теорию, которая, объясняя эти факты, содержала бы нью- тоновскую механику как предельный случай для малых скоростей

Это и удалось сделать А. Эйнштейну, который пришел к выводу о том, что мирового эфира — особой среды, кото- рая могла бы быть принята в качестве абсолютной системы, — не существует. Наличие постоянной скорости распро- странения света в вакууме находилось в согласии с уравнениями Максвелла.

Таким образом, А. Эйнштейн зало- жил основы специальной теории от- носительности. Эта теория представ- ляет собой современную физическую теорию пространства и времени, в ко- торой, как и в классической ньютонов- ской механике, предполагается, что вре- мя однородно (см. § 13), а пространство однородно (см. § 9) и изотропно (см.

§ 19). Специальная теория относитель- ности часто называется также реляти- вистской теорией, а специфические явления, описываемые этой теорией, — релятивистскими эффектами.

В основе специальной теории отно- сительности лежат постулаты Эйнш- тейна, сформулированныеимв 1905 г.

I.Принципотносительности:ни- какие опыты (механические, электри- ческие, оптические), проведенные внут- ри данной инерциалыюй системы от- счета, не дают возможности обнару- жить, покоится ли эта система или дви- жется равномерно и прямолинейно; все законыприроды 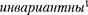по отно- шению к переходу от одной инерциаль- ной системы отсчета к другой.

II. Принцип инвариантности ско- рости света: скорость светаввакууме не зависит от скорости движения источ- ника света или наблюдателя и одинакова вовсехинерциальныхсистемахотсчета. Первый постулат Эйнштейна, явля-

ясь обобщением механического прин-

1 Инвариантные величины — величины, име- ющие одно и то же числовое значение во всех системах отсчетах.

ципа относительности (принципа отно- сительности Галилея) на любые физи- ческие процессы, утверждает, таким образом, что физические законы инва- риантны по отношению к выбору инер- циальной системы отсчета, а уравнения, описывающие эти законы, одинаковы по форме во всех инерциальных систе- мах отсчета. Согласно этому постулату, все инерциальные системы отсчета со- вершенно равноправны, т.е. явления

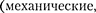
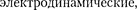
оптические и др.) во всех инерциальных системах отсчета протекают одинаково. Согласно второму постулату Эйнш-

тейна, скорости света —

фундаментальноесвойствоприроды,ко- торое констатируется как опытный факт. Специальная теория относительно- сти потребовала отказа от привычных представлений о пространстве и време- на, принятых в классической механике, поскольку они противоречили принци- пу постоянства скорости света. Потеря- ло смысл не только абсолютное про-

странство, но и абсолютное время.

Постулаты Эйнштейна и теория, построенная на их основе, установили новый взгляд на мир и новые простран- ственно-временные представления, та- кие, например, как относительность длин и промежутков времени, относи- тельность одновременности событий. Эти и другие следствия из теории Эйн- штейна находят надежное эксперимен- тальное подтверждение, являясь тем самым обоснованием постулатов Эйн- штейна — обоснованием специальной теории относительности.

§ 36. Преобразования Лоренца

Анализ явлений в инерциальных си- стемах отсчета, проведенный А. Эйнш- тейном на основе сформулированных

им постулатов, показал, что классичес- кие преобразования Галилея несовме- стимы с ними и, следовательно, долж- ны быть заменены преобразованиями, удовлетворяющими постулатам теории относительности.

Для иллюстрации этого вывода рас- смотрим две инерциальные системы отсчета: К (с координатами х, у, z) и К' (с координатами х', у', z'), движущую- ся относительно К (вдоль оси х) со ско- ростью v = const (рис. 61). Пусть в на- чальный момент времени t = t' = 0, ког- да начала координат 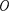и О' совпадают, излучается световой импульс. Согласно второму постулату Эйнштейна, скорость света в обеих системах одна и та же и равна с. Поэтому если за время t в сис- теме K сигнал дойдет до некоторой точ- ки А (см. рис. 61), пройдя расстояние

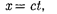(36.1)

то в системе К' координата светового импульса в момент достижения точ- ки А

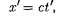(36.2)

где t' — время прохождения светового импульса от начала координат до точ- ки А в системе К'. Вычитая (36.1) из (36.2), получим

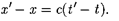
Так как х' х (система К' переме- щается по отношению к системе К), то

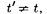
т. е. отсчет времени в системах К и К' различен— отсчет времени имеет от- носительныйхарактер (в классической

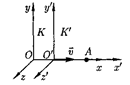Рис. 61

физике считается, что время во всех инерциальных системах отсчета течет одинаково, т.е. t = t').

Эйнштейн показал, что в теории от- носительности классические преобра- зования Галилея, описывающие пере- ход из одной инерциальной системы отсчета к другой:

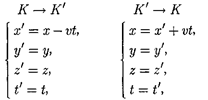
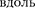
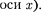заменяются преобразованиями Лорен- ца, удовлетворяющими постулатам Эйнштейна (формулы представлены для случая, когда К' движется относи- тельно К со скоростью v

Эти преобразования предложены Лоренцем в 1904 г., еще до появления теории относительности, как преобра- зования, относительно которых уравне- ния Максвелла (см. § 139) инвариантны. Преобразования Лоренца имеют вид

(36.3)

Из сравнения приведенных уравне- ний вытекает, что они симметричны и отличаются лишь знаком при v. Это очевидно, так как если скорость движе- ния системы К' относительно системы К равна v, то скорость движения К от- носительно К' равна — v.

Из преобразований Лоренца вытека- ет также, что при малых скоростях (по сравнению со скоростью с), т.е. когда (3 1, онипереходят в классические пре- образования Галилея (в этом заключает- ся суть принципасоответствия), кото- рые являются, следовательно, предель- ным случаем преобразований Лоренца. При v > с выражения (36.3) для t, x', t' теряют физический смысл (становятся мнимыми). Это находится, в свою оче- редь, в соответствии с тем, что движение со скоростью, большей скорости распро- странения света в вакууме, невозможно.

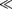
Из преобразований Лоренца следу- ет очень важный вывод о том, что как расстояние, так и промежуток времени между двумя событиями меняются при переходе от одной инерциальной сис- темы отсчета к другой, в то время как в рамках преобразований Галилея эти ве- личины считались абсолютными, не из- меняющимися при переходе от систе- мы к системе.

Кроме того, как пространственные, так и временные преобразования [см. (36.3)] не являются независимыми, по- скольку в закон преобразования коор- динат входит время, а в закон преобра- зования времени — пространственные координаты, т.е. устанавливается вза- имосвязь пространства и времени. Та- ким образом, теория Эйнштейна опери- рует не с трехмерным пространством, к которому присоединяется понятие вре- мени, а рассматривает неразрывно свя- занные пространственные и временные координаты, образующие четырехмер- ное пространство-время.

§ 37. Следствия

из преобразований Лоренца

1. Одновременность событий в раз- ных системах отсчета.Пусть в систе-

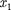
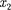
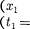
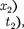ме К в точках с координатами и в моменты времен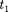и и 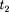происходят два события. В системе К' им соответству- ют координаты 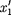и 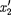и моменты вре- мен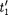и и 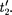Если события в системе К происходят в одной точке = и яв- ляются одновременными то, согласно преобразованиям Лоренца (36.3),

т.е.этисобытияявляютсяодновремен- ными ипространственно совпадающи- ми для любой инерциальиой системы отсчета.

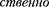
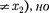ЕслисобытиявсистемеКпростран- разобщены 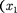одно- временны 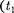= 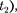то в системе К', со- гласно преобразованиям Лоренца (36.3),

2. Длительность событий в разных системах отсчета.Пусть в некоторой точке (с координатой х), покоящейся относительно системы К, происходит событие, длительность которого (раз- ность показаний часов в конце и нача- ле события) т = 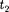— 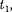где индексы 1 и 2 соответствуют началу и концу собы- тия. Длительность этого же события в системе К'

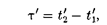(37.1)

причем началу и концу события, соглас- но (36.3), соответствуют

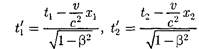(37.2)

Подставляя (37.2) в (37.1), получим

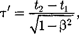
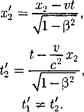
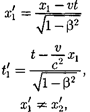или

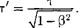(37.3)

Таким образом, в системе К' эти со- бытия, оставаясь пространственнора-

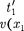
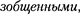оказываютсяинеодновре- менными. Знак разности 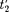— опреде- ляется знаком выражения — 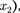поэтому в различных точках системы от- счета 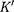(при разных v) разность 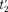— 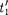будет различной по величине и может отличаться по знаку. Следовательно, в одних системах отсчета первое событие может предшествовать второму, в то время как в других системах отсчета, наоборот, второе событие предшеству- ет первому. Сказанное, однако, не отно- сится к причинно-следственным собы- тиям, так как можно показать, что по- рядок следования причинно-следствен- ных событий одинаков во всех инерци- альных системах отсчета.

Из соотношения (37.3) вытекает, что т < 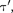т.е. длительность события, про- исходящеговнекоторойточке,наимень- шаявтой 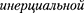системеотсче- та, относительно которой эта точка неподвижна. Этот результат может быть еще истолкован следующим образом: интервал времени т', отсчитанный по часам в системе К', с точки зрения на- блюдателя в системе К, продолжитель- нее интервала т, отсчитанного по его часам. Следовательно, часы, движущи- еся относительно инерциальной систе- мыотсчета, идутмедленнеепокоящих- ся часов, т.е. ход часов замедляется в системе отсчета, относительно которой часы движутся.

На основании относительности по- нятий «неподвижная» и «движущаяся»

системы соотношения для 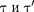обра- тимы. Из (37.3) следует, что замедле- ние хода часов становится заметным лишь при скоростях, близких к скорос- ти распространения света в вакууме.

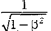В связи с обнаружением релятивис- тского эффекта замедления хода часов в свое время возникла проблема «пара- докса часов» (иногда рассматривается как «парадокс близнецов»), вызвавшая многочисленные дискуссии. Предста- вим себе, что осуществляется космиче- ский полет к звезде, находящейся на рас- стоянии 500 световых лет (расстояние, на которое свет от звезды до Земли до- ходит за 500 лет), со скоростью, близ- кой к скорости света 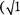— (З2 = 0,001). По земным часам полет до звезды и об- ратно продлится 1000 лет, в то время как для системы корабля и космонавта в нем такое же путешествие займет все- го 1 год. Таким образом, космонавт воз- вратится на Землю в раз более

молодым, чем его брат-близнец, остав- шийся на Земле.

Это явление, получившее название парадокса 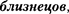в действитель- ности парадокса не содержит. Дело в том, что принцип относительности ут- верждает равноправность не всяких систем отсчета, а только 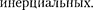Неправильность рассуждения состоит в том, что системы отсчета, связанные с близнецами, не эквивалентны: земная система 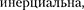а корабельная — неинерциальна, поэтому к ним принцип относительности неприменим.

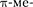Релятивистский эффект замедления хода часов является реаль- ным и получил экспериментальное под- тверждение при изучении нестабиль- ных, самопроизвольно распадающихся элементарных частиц в опытах с зонами. Среднее время жизни покоя- щихся тс-мезонов (по часам,движущим-

ся вместе с ними) т 2,2 • 10 с. Сле- довательно, образующиеся в верхних слоях атмосферы (на высоте 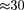км) и движущиеся со скоростью, близкой к скорости с, должны были бы проходить расстояния ст 6,6 м, т.е. не могли бы достигать земной поверх- ности, что противоречит действительно- сти. Объясняется это релятивистским эффектом замедления хода времени: для земного наблюдателя срок жизни

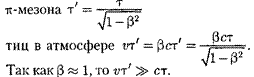
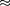
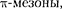
, а путь этих час-

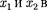
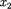
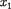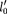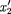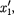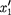3. Длина тел в разных системах от- счета. Рассмотрим стержень, располо- женный вдоль оси х' и покоящийся от- носительно системы К'. Длина стерж- ня в системе К' будет = — где и 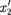— не изменяющиеся со временем t' координаты начала и конца стержня, а индекс 0 показывает, что в системе от- счета К' стержень покоится. Определим длину этого стержня в системе К, от- носительно которой он движется со скоростью v. Для этого необходимо из- мерить координаты его концов системе 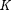в один и тот жемомент вре- мени t. Их разность 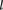— — и опре- делит длину стержня в системе К. Ис- пользуя преобразования Лоренца (36.3), получим

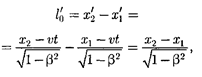
т.е.

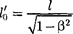(37.4)

Таким образом, длина стержня, из- меренная в системе, относительно ко-

торой он движется, оказывается мень- ше длины, измеренной в системе, отно- сительно которой стержень покоится. Если стержень покоится в системе К, то, определяя его длину в системе К', опять-таки придем к выражению (37.4). Из выражения (37.4) следует, что линейный размер тела, движущегося относительно инерциальной системы отсчета, уменьшается в направлении

движения в 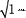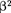раз, т.е. так назы- ваемое лоренцево сокращение длины тем больше, чем больше скорость дви- жения. Из второго и третьего уравне- ний преобразований Лоренца (36.3) следует, что

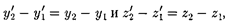
т.е. поперечные размеры тела не зави- сятотскоростиегодвиженияиодина- ковыво всех инерциалъных системах от- счета. Такимобразом, линейные разме- ры тела наибольшие в той инерциаль- ной системе отсчета, относительно которой тело покоится.

4. Релятивистский закон сложения скоростей. Рассмотрим движение ма- териальной точки в системе К', в свою очередь движущейся относительно си- стемы К со скоростью v. Определим ско- рость этой же точки в системе К. Если в системе К движение точки в каждый момент времени t определяется коорди- натами х, у, z, а в системе К' в момент времени t' — координатами х', у', z', то

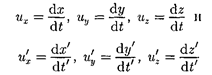представляют собой соответственно проекции на оси х, у, и 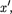у', z' вектора скорости рассматриваемой точки отно- сительно систем К и К'. Согласно пре- образованиям Лоренца (36.3),

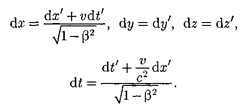
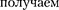Произведя соответствующие преоб- разования, релятивистский закон сложения скоростей специаль- ной теории относительности:

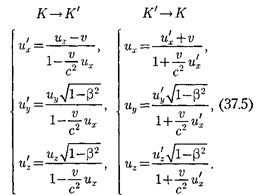
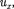Если материальная точка движется параллельно оси х, то скорость и отно- сительно системы К совпадает с а скорость 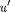относительно К' — с 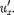Тог- да закон сложения скоростей примет вид

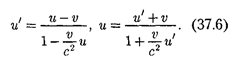
Легко убедиться в том, что если ско- рости v, и' и и малы но сравнению со скоростью с, то формулы (37.5) и (37.6) переходят в закон сложения скоростей в классической механике [см. (34.4)]. Таким образом, законы релятивистской механики в предельном случае для ма- лых скоростей (по сравнению со скоро- стью распространения света в вакууме) переходят в законы классической фи- зики, которая, следовательно, является

частным случаем механики Эйнштей- на для малых скоростей.

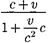Релятивистский закон сложения скоростей подчиняется второму посту- лату Эйнштейна (см. § 35). Действи- тельно, если и' = с, то формула (37.6)

примет вид и= = с (аналогич-

но можно показать, что при и = с ско- рость и' также равна с). Этот результат свидетельствует о том, что релятивист- ский закон сложения скоростей нахо- дится в согласии с постулатами Эйнш- тейна.

Докажем также, что если складывае- мые скорости сколь угодно близки к ско- рости с, то их результирующая скорость всегда меньше или равна с. В качестве примера рассмотрим предельный случай 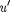= v= с. После подстановки в форму- лу (37.6) получим и — с. Таким образом, при сложении любых скоростей резуль- тат не может превысить скорости света с в вакууме. Скорость света в вакууме естьпредельнаяскорость, которую не- возможно превысить. Скорость света в какой-либо среде, равная — (п — абсо-

лютныи показатель преломления сре- ды), предельной величиной не является (подробнее см. § 189).

§ 38. Интервал между событиями

Преобразования Лоренца и след- ствия из них приводят к выводу об от- носительности длин и промежутков времени, значение которых в различ- ных системах отсчета разное. В то же время относительный характер длин и промежутков времени в теории Эйнш- тейна означает относительность отдель- ных компонентов какой-то реальной физической величины, независящейот системы отсчета, т. е. являющейся инва-

риантной по отношению к преобразо- координат.

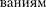В четырехмерном пространстве Эйн- штейна, в котором каждое событие ха- рактеризуется четырьмя координатами

{х,у, z,t), такой физической величиной является интервал между двумя собы- тиями:

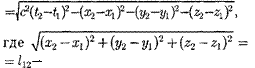
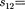(38.1)

расстояние между точками трех- мерного пространства, в которых эти события произошли. Введя обозначение 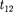= 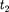— 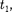получим

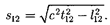
Покажем, что интервал между дву- мя событиями одинаков во всех инер- циальных системах отсчета. Обозначив

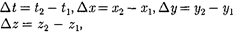и выражение (38.1) можно

записать в виде

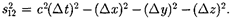
Интервал между теми же события- ми в системе К' равен

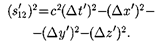(38.2)

Согласно преобразованиям Лоренца (36.3),

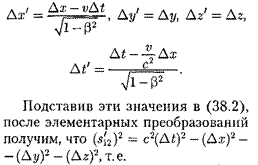
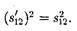
Обобщая полученные результаты, можно сделать вывод, что интервал, определяя пространственно-времен- ные соотношения между событиями, является инвариантом при переходе от одной инерциальной системы отсчета к другой. Инвариантность интервала означает, что, несмотря на относи- тельность длин и промежутков време- ни, течение событий носит объектив- ный характер и не зависит от системы отсчета.

Теория относительности, таким об- разом, сформулировала новое пред- ставление о пространстве и времени. Пространственно-временные отноше- ния являются не абсолютными величи- нами, как утверждалось в механике Галилея — Ньютона, а относительными. Следовательно, представления об абсо- лютном пространстве и времени явля- ются несостоятельными. Кроме того, инвариантность интервала между дву- мя событиями свидетельствует о том, что пространство и время органически связаны между собой и образуют еди- ную форму существования материи —

«пространство — время». Пространство и время не существуют вне материи и независимо от нее.

Дальнейшее развитие теории отно- сительности {общая теория относи- тельности, или теория тяготения) показало, что свойства пространства- времени в данной области определяют- ся действующими в ней полями тяго- тения. При переходе к космическим масштабам геометрия пространства- времени не является евклидовой (т.е. не зависящей от размеров области

«пространство — время»), а изменяется от одной области к другой в зависимо- сти от концентрации масс в этих облас- тях и их движения.

§ 39. Основной закон релятивистской динамики материальной точки

Изпринципа относительности Эйн- штейна (см. §35), утверждающего ин- вариантность всех законов природы при переходе от одной инерциальной системы отсчета к другой, следует ус- ловие инвариантности уравнений фи- зических законов относительно преоб- разований Лоренца. Основной закон

динамики Ньютона 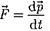оказывает- ся также инвариантным поотношению к преобразованиям Лоренца, если в нем справа стоит производная повремени от релятивистского импульса.

Основной закон релятивистской динамики материальной точки имеет вид

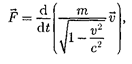(39.1)

или

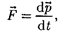(39.2)

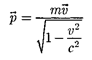где

(39.3)

— релятивистский импульс матери- альной точки (га — масса материальной точки).

Отметим, что уравнение (39.2) внешне совпадает с основным уравне- нием ньютоновской механики (6.7). Однако физический смысл его другой: справа стоит производная по времени от релятивистского импульса, опреде- ляемого формулой (39.3). Таким обра- зом, уравнение (39.1) инвариантно по

отношению к преобразованиям Лорен- ца и, следовательно, удовлетворяет принципу относительности Эйнштей- на. Следует учитывать, что ни импульс, ни сила не являются инвариантными величинами. Более того, в общем слу- чае ускорение не совпадает по направ- лению с силой.

Анализ формул (39.3) и (39.1) пока- зывает, что при скоростях, значитель- но меньших скорости с, уравнение (39.1) переходит в основной закон [см. (6.5)] классической механики. Следова- тельно, условием применимости зако- нов классической (ньютоновской) ме- ханики является условие 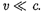Зако- ны классической механики получают- ся как следствие теории относительнос- ти для предельного случая 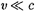(Ф°Р~ мально переход осуществляется при 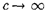). Таким образом, классическая механика — это механика макротел, движущихся с малыми скоростями (по сравнению со скоростью света в вакуу- ме).

§ 40. Энергия

В релятивистской механике

Найдем кинетическую энергию ре- лятивистской частицы. Элементарная работа силы F на малом перемещении 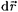равна 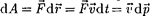[учли

основной закон релятивистской дина- мики (39.2)]. Тогда

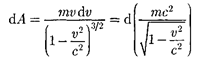
(этот результат можно проверить диф- ференцированием).

Приращение кинетической энергии материальной точки на элементарном перемещении равно элементарной ра-

боте на том же перемещении (см. § 12):

dT=dA. Тогда

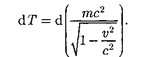
Интегрируя это выражение, получим

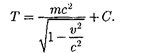
Поскольку кинетическая энергия при v — 0должна обращаться внуль, то постоянная интегрирования 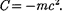Следовательно, кинетическая энергия релятивистской частицы

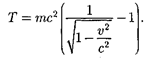(40.1)

Выражение (40.1) при скоростях 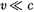переходит вклассическое:

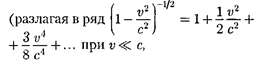
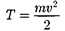(40.2)

правомерно пре- небречь слагаемыми второго порядка малости).

Полная энергия свободной частицы,

т.е. частицы, на которую не действуют силы,

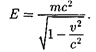(40.3)

Отметим, что в полную энергию Е не входит потенциальная энергия тела во внешнем силовом поле. Полная энер- гия частицы в разных системах отсчета различна.

В случае покоящейся частицы (v = 0) из формулы (40.3) найдем, что

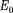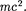= (40.4)

Величина, определяемая выражени- ем (40.4), называется энергией покоя. Значения т и 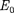не зависят от выбора инерциалыюй системы отсчета. В энер- гию покоя, как и в полную энергию (40.3), не входит энергия тела во внеш- нем силовом поле. В классической ме- ханике энергия покоя 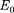не учитывает- ся, считая, что при v = 0 энергия поко- ящегося тела равна нулю.

Как энергия Е, так и импульс р реля- тивистской частицы имеют различные значения в разных системах отсчета. Но существует величина Е2 — 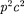= inv, являющаяся инвариантной (имеющей одно то же значение в разных систе- мах отсчета):

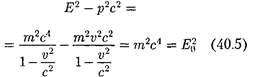[учли формулы (39.3), (40.3) и(40.4)]. Согласно формуле (40.5), получим

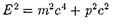Е2 — р2с2 = т2с4, откуда связь между энергией и импульсом

или

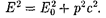(40.6)

Извыражений (40.3), (40.1) и (40.4) следует, что полная энергия системы

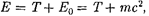(40.7)

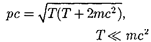т.е. складывается из ее кинетической энергии и энергии покоя. Подставив (40.7) в (40.6), получим

(40.8)

откуда следует, что при выра- жение (40.8) переходит в ньютоновское

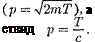при 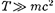приобрета-

Согласно формуле (40.4), масса тела и его энергия покоя связаны соотноше- нием 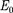= 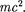Это означает, что вся- кое изменение массы тела Am сопро- вождается изменением энергии покоя 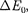и эти изменения пропорциональ- ны друг другу, т. е.

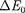
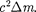(40.9)

Выражение (40.9) носит название закона взаимосвязи массы и энергии

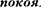
Чтобы охарактеризовать прочность связи и устойчивость системы каких- либо частиц (например, атомного ядра как системы из протонов и нейтронов), вводят понятие энергии связи. Энергия связи