Электрический поверхностный эффект в плоской шине
Пусть вдоль шины направлен переменный ток. Положительное направление тока и расположение осей декартовой системы координат даны на рис5.3.
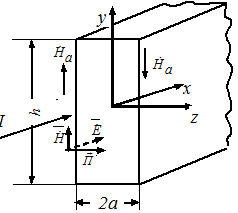
Рис.5.3
По закону полного тока найдем Напряжённость магнитного поля на поверхности шины. Так как в данной задаче, как и в предыдущей, h >2a, то при подсчете 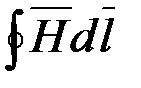 можно в первом приближении пренебречь составляющей интеграла вдоль горизонтальных сторон шириной 2а.
можно в первом приближении пренебречь составляющей интеграла вдоль горизонтальных сторон шириной 2а.
Тогда, обозначив Напряжённость поля на поверхности шины через 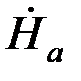 , получим
, получим 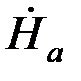 2h=İ. Отсюда
2h=İ. Отсюда 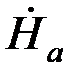 = İ/2h.
= İ/2h.
При составлении уравнений для определения постоянных интегрирования учтем, что слева от шины Напряжённость ориентирована вдоль положительного направления оси y, а справа – в отрицательном направлении оси y.
Общее решение для плоской волны:
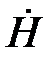 = Ċ1epz +Ċ2e-pz.
= Ċ1epz +Ċ2e-pz.
Постоянные интегрирования найдем, используя граничные условия:
при z = – а 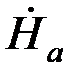 = Ċ1e-pа+ Ċ2epа,
= Ċ1e-pа+ Ċ2epа,
при z = а – 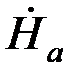 = Ċ1epа+ Ċ2e-pа
= Ċ1epа+ Ċ2e-pа
Совместное решение двух последних уравнений дает 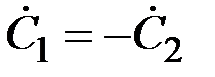 Ċ1= –
Ċ1= – 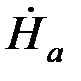 /2sh pa.
/2sh pa.
Подставим Ċ1 и Ċ2в общее решение. Будем иметь
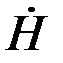 = –
= – 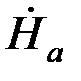 ·sh pz/sh pa = – (İ·sh pz)/( 2h ·sh pa).
·sh pz/sh pa = – (İ·sh pz)/( 2h ·sh pa).
Напряжённость электрического поля Ė направлена вдоль оси x и равна Ė = –d 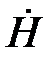 /(γ dz)
/(γ dz)
или Ė= (p İ ch pz) /(2 γ h ·sh pa).
Плотность тока в любой точке пластины
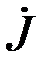 = γ Ė=pİ · ch pz /(2h ·sh pa).
= γ Ė=pİ · ch pz /(2h ·sh pa).
Минимальное значение плотности тока будет в средней плоскости шины при z = 0.
Оно равно 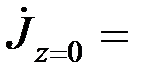 pİ/(2h ·sh pa).
pİ/(2h ·sh pa).
График изменения модуля 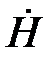 в функции от z представлен на рис. 5.4. На том же рисунке изображена вторая кривая, она дает зависимость модуля плотности тока от z.
в функции от z представлен на рис. 5.4. На том же рисунке изображена вторая кривая, она дает зависимость модуля плотности тока от z.
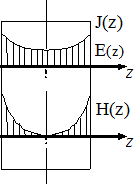
Рис.5.4
Чем толще шина, чем больше γ, μ, и ω, тем сильнее проявляется поверхностный эффект. Если частота ω очень велика, то может оказаться, что ток будет протекать только по тонкому поверхностному слою шины.
При тонких шинах и относительно небольших частотах поверхностный эффект проявляется в малой степени.
Определение активного и внутреннего индуктивного сопротивления проводников на переменном токе часто производят при помощи теоремы Умова - Пойнтинга в комплексной форме. С этой целью подсчитывают поток вектора Пойнтинга через боковую поверхность проводника на длине в один метр и делят его на квадрат тока, протекающего по проводнику, получают комплекс сопротивления проводника на единицу длины (на один метр).
Действительно, 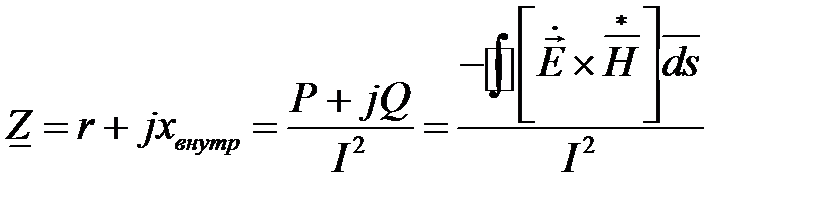 .
. 
В качестве примера определим активное и внутреннее индуктивное сопротивление прямоугольной шины длиной в один метр. Энергия в шину проникает с двух сторон. Поверхность шины с двух сторон на длине в 1 м равна 2h1.
Z=R+jX= 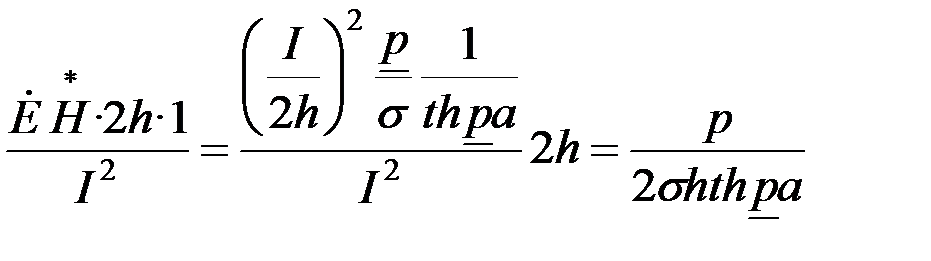 .
.
Эффект близости
Если поблизости от проводникаесть другой проводник с током, то второй проводник влияет на картину поля в первом проводнике. В результате этого влияния активное сопротивление такого провода, как правило, увеличивается по сравнению с активным сопротивлением уединенного провода. Влияние близлежащих проводников с током на сопротивления проводника называют эффектом близости.
Рассмотрим эффект близости на примере двух плоских шин, близко расположенных одна к другой (рис. 5.5, а).
Одна шина является прямым проводом, другая обратным. Если расстояние между шинами 2b такого, же порядка, что и толщина шин (2а) и много меньше высоты h, то с известной степенью приближения Напряжённость магнитного поля в пространстве между шинами в два раза больше напряженности магнитного поля от одной шины в непосредственной близости от шины. А снаружи шин Напряжённость магнитного поля примерно равна нулю.
Для того чтобы убедиться в этом, воспользуемся принципом наложения. На рис. 5.5,б дан вид на пластины с торца. Сплошные стрелки на рис. 5.5 представляют Напряжённость поля от левой шины, пунктирные от правой. В пространстве между шинами напряженности складываются, снаружи вычитаются. В результате оказывается, что Напряжённость поля в пространстве между шинами H=2·I/2h=I/h, а снаружи шин Напряжённость магнитного поля равна нулю.
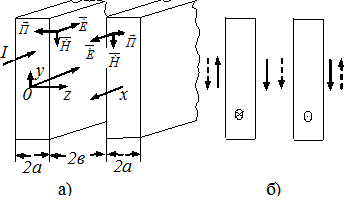
Рис.5.5
Найдем постоянные интегрирования в выражении
 = Ċ1epz +Ċ2e-pz.
= Ċ1epz +Ċ2e-pz.
При z= –a 0 = Ċ1e-pa +Ċ2epа. При z = a – İ/h = Ċ1epa +Ċ2e-pа.
Отсюда Ċ1= –İepa/(2h sh 2pa) и Ċ2= İe-pa/(2h sh 2pa).
Следовательно,
 = – İ(epa+pz–e-pa-pz)/2h sh 2pa= – İ sh p(a+z) /(h sh 2pa) и
= – İ(epa+pz–e-pa-pz)/2h sh 2pa= – İ sh p(a+z) /(h sh 2pa) и
Напряжённость электрического поля Ė=pİch p(a+z)/(γh sh 2pa).
Если придавать z значения от – а до а, то по написанным выше формулам могут быть построены кривые изменения модулей Ė и  в функции от z. Такие кривые качественно изображены на рис.5.6.
в функции от z. Такие кривые качественно изображены на рис.5.6.
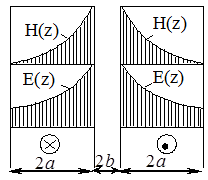
Рис.5.6
Для правой шины кривые построены на основании симметрии поля. Если не учитывать искажающего действия торцов, то электромагнитная волна в каждую из шин проникает только через поверхности их, обращенные друг к другу. Через наружные поверхности электромагнитная волна не проникает, так как там Н = 0. Комплекс сопротивления одной шины на единицу длины
Zвн.1= 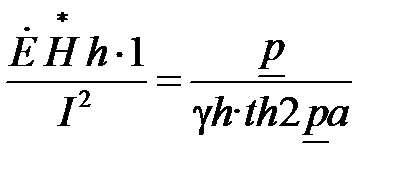 .
.
Рассмотрим числовой пример. Пусть ток в 10 а течет по двум таким же шинам, с которые рассматривали в предыдущем параграфе (h =2см, 2а = 0,1 см). Одна из шин является прямым проводом, другая обратным. Подсчитаем комплекс сопротивления одной шины на единицу длины с учетом эффекта близости и сравним его с сопротивлением уединенной шины( когда эффекта близости нет):
th 2pa = (sh 3,74+j sin 214˚)/(ch 3,74+ cos 214˚) = 1,04e-j1˚30′.
Следовательно,
Zвн.1= p/(γh th 2pa) =18,7√2ej45˚/(5,6·107·21,04·e-j1˚ 30′) = 22,5·10-4 e-j46˚ 30′;
R=15,7·10-4 Ом/м; Хвн=16,34·10-4 Ом/м.
Таким образом, влияние второй шины на поле в первой шине привело к тому, что активное сопротивление одной шины возросло с
9,5·10-4 до 15,7·10-4 Ом/м.
Для определения комплекса полного сопротивления единицы длины петли, образованной двумя шинами, кроме собственного сопротивления самих шин, надо учесть еще индуктивное сопротивление, обусловленное магнитным потоком, проходящим в пространстве между шинами.
Последнее равно:
Хвнешн = ωLвнешн = ω Фвнешн/I = (ωμ0H·2в·1)/I =μ0ω2в/h.
Комплекс полного сопротивления единицы длины петли
Zполн=2r вн+j (2xвн + xвнешн).
