Магнитное поле постоянных токов

Постоянный заданный ток порождает стационарное магнитноеполе, не зависящее от времени и не связанное с электрическим полем.

Уравнения магнитного поля дифференциальной форме

Уравнениями Максвелла для магнитного поля постоянного тока имеют вид:

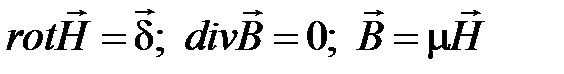. (4.1)

Магнитное поле является вихревым (непотенциальным). Магнитное поле не имеет источников, линии вектора магнитной индукции непрерывны и замкнуты.

Векторный потенциал магнитного поля

Введем векторный потенциал магнитного поля 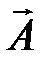, который связан с вектором магнитной индукции соотношением:

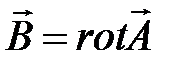. (4.2)

Получим уравнение для векторного потенциала в однородной среде.

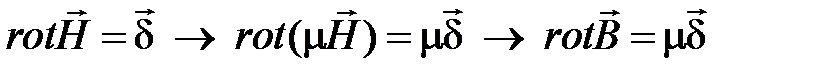. (4.3)

Подставляя (4.2) в (4.3), имеем:

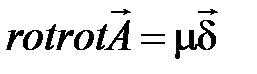. (4.4)

В соответствии с правилами векторной алгебры имеем:

,

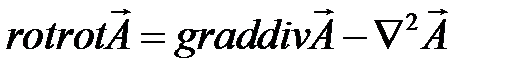тогда уравнение (4.4) примет вид:

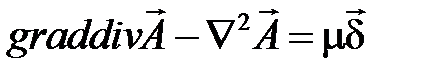(4.5)

Чтобы уравнение (4.5) стало как можно более простым пПримем .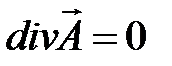

В этом случае уравнение (4.5) имеет вид

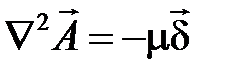. (4.6)

Одному вВекторному уравнению (4.6) соответствуют три скалярных относительно проекций вектора 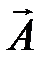в выбранной системе координат.

В декартовой системе получим:

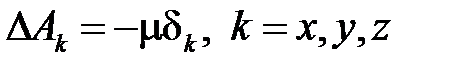(4.7)

Выражения (4.7) по форме записи совпадают с уравнением Пуассона для скалярной потенциальной функции 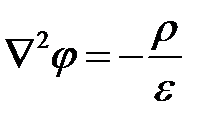. Между уравнениями существует математическая аналогия. Следовательно, решение (4.7) формально совпадает с решением уравнения Пуассона для электростатического поля.

Решение уравнения Пуассона известно и имеет вид .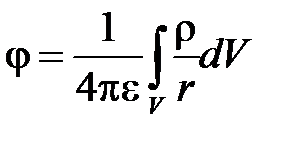

Используя математическую аналогию между величинами запишем решение уравнений (4.7):

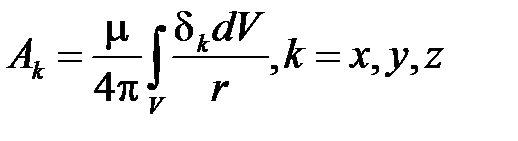, (4.8)

где 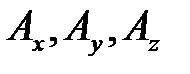— проекции вектора ;

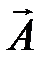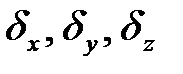― проекции вектора плотности тока;

r ― расстояние от элемента тока до точки, в которой определяется магнитное поле.

Объединя соотношения (4.8), получим решение:

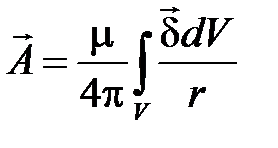. (4.9)

Решение в виде (4.8) и (4.9) получается и используется при условии существования токов в ограниченном объеме пространства, что на практике всегда имеет место. При этом, как ясно из (4.8) и (4.9), величина векторного потенциала убывает по мере удаления от области, занятой токами, в бесконечность не медленнее, чем 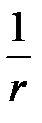. Так как магнитная индукция определяется зависимостью 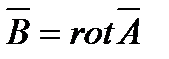, а операция 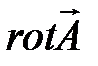есть векторно-пространственная производная, то 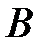и соответственно H убывают с увеличением радиуса r не медленнее, чем .

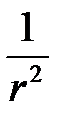Рассмотрим расчёт магнитного поля в случае линейного тока (рис.4.1).

Пусть известна плотность линейного тока δ. Тогда

,

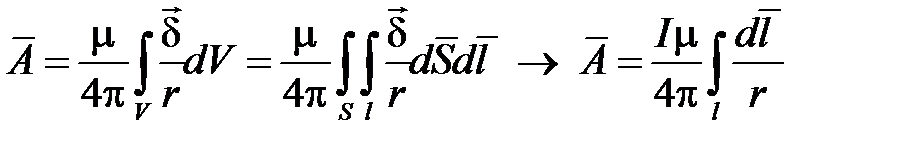так как ток .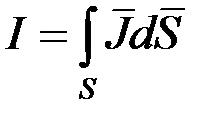

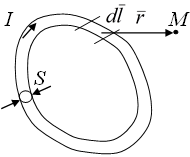
Рис.4.1.Контур с током

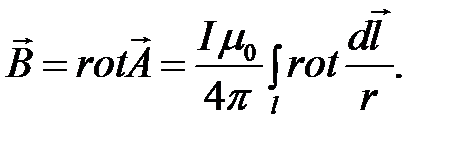(4.10)

Определим подынтегральное выражение в (4.10).

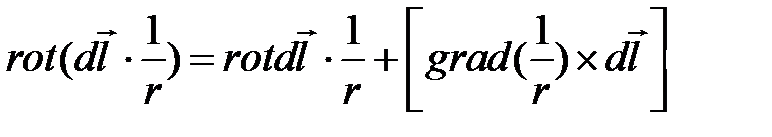
Соответственно

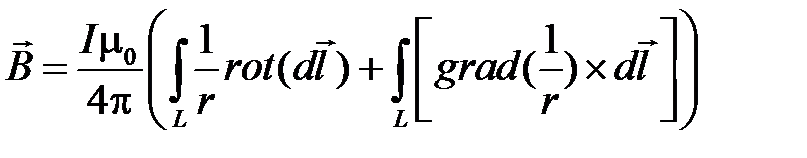
Так как dl не зависит от положения точки М, в которой находим ротор, то 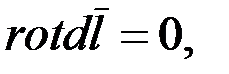а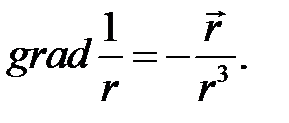

Подставив полученные результаты в уравнение (4.10) получаем

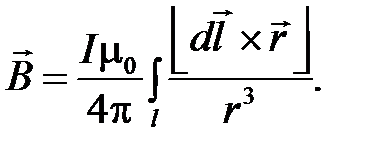
Это интегральная формулировка закона Био-Савара-Лапласа, непосредственно связывающего напряжённость магнитного поля с линейным распределением тока (рис. 4.2).

Рис. 4.2. К закону Био-Савара-Лапласа

На основе закона Био-Савара-Лапласа выполняется расчёт магнитного поля слож­ных систем проводников с токами.

Выражение магнитного потока и энергии

Через векторный потенциал

Магнитный поток, пронизывающий через поверхность S (рис. 4.3) равен:

индукцию 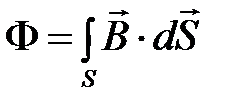. (4.11)

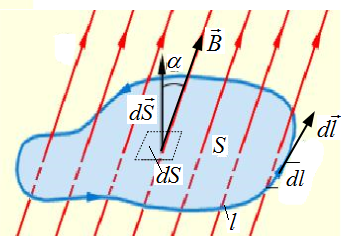
Рис. 4.3. К определению магнитного потока

На основании теоремы Стокса поверхностный интеграл может быть преобразован в линейный:

Используя теорему Стокса, получим: 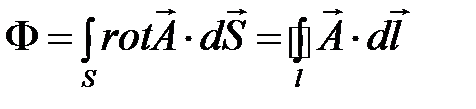. (4.12)

(4.11)

Магнитный поток 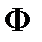сквозь поверхность 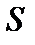равен линейному интегралу от векторного потенциала 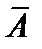по замкнутому контуру, ограничивающему эту поверхность.

Определение потока по (4.12) часто имеет преимущества по сравнению с определением потока через магнитную индукцию (4.11). Соотношением (4.11) можно пользоваться в том случае, когда известно значение 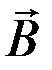в любой точке поверхности S, тогда как для вычисления потока с помощью соотношения (4.12) достаточно знать значение на контуре и не требуется значения 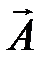в точках внутри контура.

Для вычисления магнитного потока 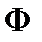по формуле (4.11) достаточно знать векторный потенциал 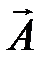только на контуре, ограничивающем эту поверхность.

Известно, что с магнитным полем связана энергия, распределенная в пространстве с плотностью

.

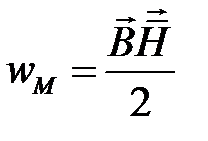В некоторой области V энергия определяется интегралом

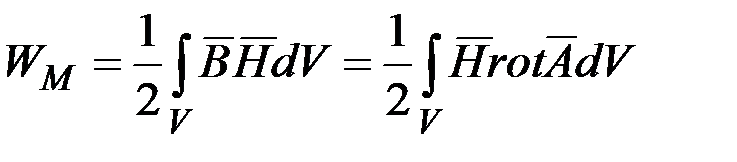, так как .

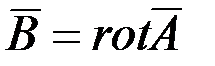Используя равенство 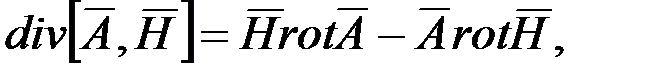получим

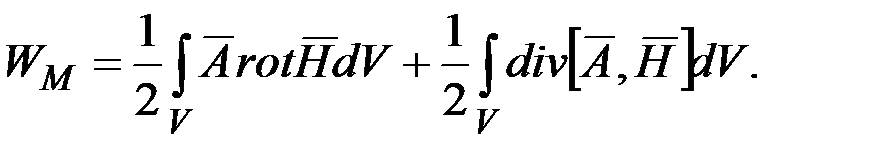
Преобразуем второе слагаемое по теореме Остроградского-Гаусса

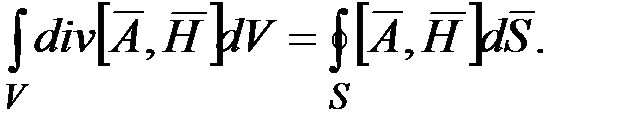
При учете всей энергии поля подынтегральное выражение в последней формуле устремляется к нулю, так как произведение векторного потенциала и напряжености магнитного поля убывает быстрее, чем r ^–2, а площадь увеличивается пропорционально r². Таким образом, с учетом 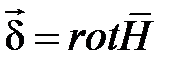получаем:

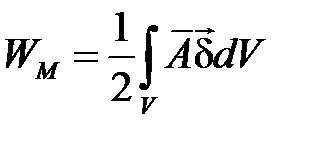. (4.1213)

Необходимо отметить, что величина 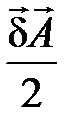не является плотностью энергии. Если предположить, что 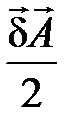— плотность энергии магнитного поля, то немедленно следует, что вся энергия магнитного поля заключена в области, где 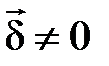(например, в проводах). Однако физически данное утверждение неверно, так как энергией обладают все точки, где 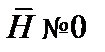. Выражение (4.1213) просто устанавливает связь между энергией поля и векторным потенциалом .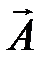