Внутренняя энергия газа Ван-дер-Ваальса
Энергия одного моля газа Ван-дер-Ваальса слагается из:
• внутренней энергии молекул газа;
• кинетической энергии теплового движения центра масс молекул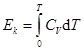 
• потенциальной энергии взаимного притяжения молекул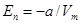 
Потенциальная энергия притяжения молекул равна работе, необходимой для разведения молекул на бесконечное расстояние друг от друга. В этом конечном состоянии молекулы не взаимодействуют друг с другом, а потенциальную энергию можно считать равной нулю.
Дополнительное давление газа Ван-дер-Ваальса за счет взаимного притяжения молекул равно a/Vm2, тогда потенциальная энергия взаимодействия равна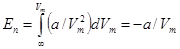 
;
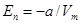
Vm – молярный объем: Vm = V/n, n = m/m.
Знак «минус» указывает на то, что между молекулами действуют силы притяжения.
Полная энергия одного моля газа Ван-дер-Ваальса :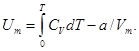 
Если СV не зависит от температуры, тополная энергия одного моля:
Um = CV Т– a/Vm
Принципиальное значение уравнения Ван-дер-Ваальса определяется следующими обстоятельствами:
1) Уравнение было получено из модельных представлений о свойствах реальных газов и жидкостей, а не явилось результатом эмпирического подбора функцииf(P,V,T), описывающей свойства реальных газов;
2) Уравнение долго рассматривалось как некоторый общий вид уравнения состояния реальных газов, на основе которого было построено много других уравнений состояния;
3) С помощью уравнения Ван-дер-Ваальса впервые удалось описать явление перехода газа в жидкость и проанализировать критические явления.
В этом отношении уравнение Ван-дер-Ваальса имеет преимущество даже перед более точными уравнениями в вириальной форме. Причиной недостаточной точности уравнения Ван-дер-Ваальс считал ассоциацию молекул в газовой фазе, которую не удается описать, учитывая зависимость параметров a и b от объема и температуры, без использования дополнительных постоянных.
После 1873 г. сам Ван-дер-Ваальс предложил еще шесть вариантов своего уравнения, последнее из которых относится к 1911 г. и содержит пять эмпирических постоянных. Две модификации уравнения предложил Клаузиус, и обе они связаны с усложнением вида постоянной b. Больцман получил три уравнения этого типа, изменяя выражения для постоянной a.
Всего известно более сотни подобных уравнений, отличающихся числом эмпирических постоянных, степенью точности и областью применимости
Выяснилось, что ни одно из уравнений состояния, содержащих менее 5 индивидуальных постоянных, не оказалось достаточно точным для описания реальных газов в широком диапазоне P, V, T, и все эти уравнения оказались непригодными в области конденсации газов.
Из простых уравнений с двумя индивидуальными параметрами неплохие результаты дают уравнения Дитеричи и Бертло.
Билет 29
Реальные газы
Модель идеального газа, используемая в молекулярно-кинетической теории газов, позволяющая описывать поведение разрежённых реальных газов при достаточно высоких температурах и низких давлениях. При выводе уравнения состояния идеального газа размерами молекул и их взаимодействием друг с другом пренебрегают. Повышение давления приводит к уменьшению среднего расстояния между молекулами, поэтому необходимо учитывать объём молекул и взаимодействие между ними. При высоких давлениях и низких температурах указанная модель идеального газа непригодна.
При рассмотрении реальных газов – газов, свойства которых зависят от взаимодействия молекул, надо учитывать силы межмолекулярного взаимодействия. Они проявляются на расстояниях ≤10-9 м. и быстро убывают при увеличении расстояния между молекулами. Такие силы называются короткодействующими.
В ХХ в., по мере развития и представлений о строении атома и квантовой механики, было выяснено, что между молекулами вещества одновременно действуют силы притяжения и силы отталкивания. Силы отталкивания считаются положительными, а силы взаимного притяжения – отрицательными.