Теплоёмкость тела характеризуется количеством теплоты, необходимой для нагревания этого тела на один граду

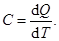
Размерность теплоемкости: [C] = Дж/К.

Теплоёмкость – величина неопределённая, поэтому пользуются понятиями удельной и молярной теплоёмкости.

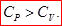Удельная теплоёмкость С_уд – есть количество теплоты, необходимое для нагревания единицы массы вещества на
1 градус [C_уд] = Дж/К.

Для газов удобно пользоваться

Опр.25. молярной теплоемкостью С_μ - количество теплоты, необходимое для нагревания
1 кмоля газа на 1 градус

Теплоёмкость термодинамической системы зависит от того, как изменяется состояние системы при нагревании.

Если газ нагревать при постоянном объёме, то всё подводимое тепло идёт на нагревание газа, то есть изменение его внутренней энергии.
Теплоёмкость при постоянном объёмеС_V

С_Р – теплоемкость при постоянном давлении.

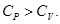
Теплоемкость при постоянном объёме Теплоемкость при постоянном объёме будет равна: 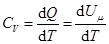Из этого следует, что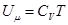

В случае идеального газа справедлива формула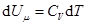

Внутренняя энергия идеального газа является только функцией температуры (и не зависит от V, Р и тому подобным), поэтому формула справедлива для любого процесса.

Для произвольной идеальной массы газа: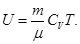

При изобарическом процессе кроме увеличения внутренней энергии происходит совершение работы газом 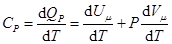Из основного уравнения молекулярно-кинетической теории 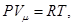При изобарическом процессе Р = const.
Тогда получим 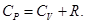Это уравнение Майера для одного моля газа

Из него следует, что физический смысл универсальной газовой постоянной в том, что R – численно равна работе, совершаемой одним молем газа при нагревании на один градус при изобарическом процессе

формулу Майера для удельных теплоёмкостей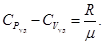

10. Применение первого начала термодинамики к изохорному, изобарному, изотермическому и адиабатическому процессам.

изобарного процесса.

1) P=const; m=const.

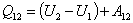(53.1)

- интегральная запись первого начала термодинамики для изобарного процесса.

В изобарном процессе всё полученное системой количество теплоты идёт на приращение внутренней энергии и совершение работы против внешних сил.

Но для него также выполняется закон Гей-Люссака:

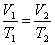(53.2)

а работа в изобарном процессе равна:

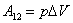(53.3)

Приращение объёма найдем из закона Гей – Люссака:

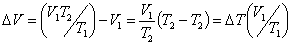(53.4)

Теперь, подставим приращение объёма при постоянном давлении и ав формулу для расчёта работы (53.3), получим:

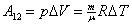(53.5)

Из определения приращения внутренней энергии получаем:

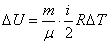(53.6)

Теперь сравним соотношения для расчёта работы (53.5) и приращения внутренней энергии (53.6) в изобарном процессе и получим формулу связи между ними:

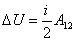(53.7)

Или

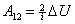(53.7)

Теперь соотношение (53.1) можем представить ещё в двух формах записи:

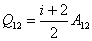(53.8)

или

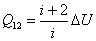(53.9)

А если выразить количество теплоты, полученное системой в изобарном процессе через молярную теплоёмкость при постоянном давлении, то получим:

Q12=(m/μ)Ср·ΔT

(53.10)

Иногда приходится разбивать реальный процесс на элементарные процессы и тогда выражение для первого начала в дифференциальной форме будет иметь вид:

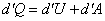(53.11)

Соотношение (53.11) удобно использовать при решениях задач по разделу термодинамика.

2) Рассмотрим изохорный процесс.

V=const; m=const; A₁₂=0; dA=0.

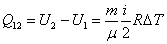(53.12)

– интегральная форма записи первого начала термодинамики для изохорного процесса.

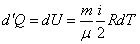(53.13)

– дифференциальная форма записи первого начала термодинамики для изохорного процесса.

Таким образом, в изохорном процессе всё полученное системой количество теплоты идёт на приращение внутренней энергии.

3) Рассмотрим изотермический процесс:

Т=const; m=const; ΔU=0, A₁₂≠0

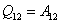(53.14)

- интегральная запись первого начала термодинамики для изотермического процесса.

В изотермическом процессе всё полученное системой количество теплоты идёт на совершение работы против внешних сил.

4) Адиабатный процесс.

По определению - адиабатный процесс происходит без теплообмена с окружающей средой: Q₁₂=0, тогда интегральная форма записи первого начала термодинамики для адиабатного процесса имеет вид:

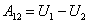(53.15)

Из соотношения (53.15) следует:

в адиабатном процессе работа совершается только за счёт убыли внутренней энергии.

Представим соотношение (53.15) в другом виде, выразив в выражении для внутренней энергии число степеней свободы через показатель адиабаты:

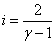(53.16)

Теперь

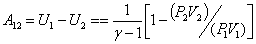(53.17)

А в дифференциальной форме записи первое начало термодинамики для адиабатного процесса имеет вид:

d¢Q=0, тогда

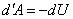11. Закон распределения молекул по скоростям (распределение Максвелла)

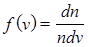функция распределения – доля молекул, приходящаяся на единичный интервал скоростей вблизи некоторого значения v, т.е. в интервале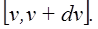

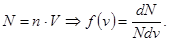
Функция распределения – вероятность того, что скорость молекул лежит в единичном интервале вблизи некоторого значения v.

Распределение Максвелла: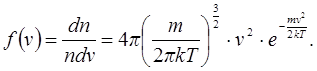

m – масса молекулы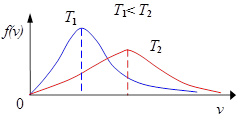

Распределение найдено с применением методов теории вероятности.

Свойства распределения Максвелла:

1. Кривая распределения имеет максимум, т.к. при малых значениях скорости v степенная функция v²растёт быстрее экспоненты, а при больших наоборот.

Экспонента в формуле распределения зависит от v²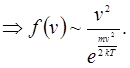

2. При увеличении температуры Т максимум распределения смещается в сторону более высоких скоростей и понижается, т.к. площадь под кривой не меняется.

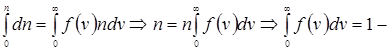Условие нормировки

3. Доля молекул, приходящихся на единичный интервал скоростей вблизи v = 0 и v = ∞, равна нулю.

Связано это с тем, что в соответствии с теорией вероятности молекулы при столкновении не могут либо только отдавать, либо только получать энергию.

4. Доля молекул, обладающих строго определённым (точным) значением скорости, равна нулю.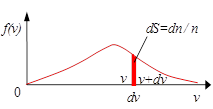

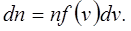
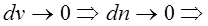
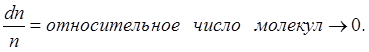
5. Распределение Максвелла по скоростям справедливо для молекул не только идеального газа, но и для реального газа, жидкости, твёрдого тела.

6. Если систему молекул поместить в силовое поле, то это силовое поле не влияет на распределение молекул по скоростям.

12. Обратимые и необратимые процессы. Круговой процесс. Тепловые двигатели и холодильные машины.