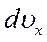Основные физические свойства жидкости
Основными физическими свойствами жидкости являются плотность, вязкость, поверхностное натяжение, удельный вес.
1) Плотность - масса жидкости приходящейся на единицу объёма
ρ = m/V, (кг/м3)
плотность несжимаемых жидкостей незначительно увеличивается с повышением давления и уменьшается с повышением температуры.
ρ Н2О= 1000 кг/м3
ρ возд.= 1,293 кг/м3
Плотность газовых смесей может быть определена из уравнения Менделеева-Клайперона:
ρ = m/V = PM/RT , (кг/м3)
2) Удельный вес γ - вес в единице объёма
γ = G/V , (Н/м3)
G = mg ; γ = mg/V = pg
3) Поверхностное натяжение:
на межфазовой поверхности жидкости существует тонкий слой (в несколько молекул), в которых возникает натяжение, т.к. молекулы жидкости находятся на поверхности, сильнее притягиваются молекулами внутренних слоёв, чем молекулами другой фазы на межфазной поверхности.
Действие сил поверхностного натяжения проявляются в стремлении жидкости уменьшать свою поверхность. На создание новой поверхности необходимо затратить некоторую работу.
Величина этой работы, т.е. для создания единицы поверхности при постоянной температуре, называется поверхностным натяжением:
= А/F, (Дж/м2)
4). При движении жидкостей и газов между отдельными их слоями происходит молекулярный обмен количеством движения, и возникают силы внутреннего трения.
|
 |
|
|
|
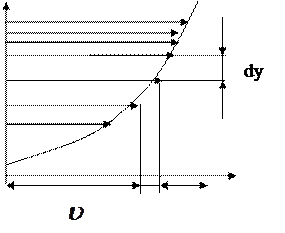
Закон Ньютона-Петрова гласит: при движении вязкой жидкости параллельными слоями действует касательное напряжение внутреннего трения, равное произведению динамического коэффициента вязкости на градиент скорости.
μ = (Н*сек/м2) = (Па*с) = Пз = 10пз = 108 спз (сантипуаз)
γ = μ/ρ (м2/с) = 104 ст (стокс)
У капельных жидкостей вязкость с увеличением температуры уменьшается, у упругих увеличивается.
Неньютоновские жидкости не подчиняются закону Ньютона-Петрова.
Ньютоновские жидкости: спирт, ртуть, вода, бензин.
Неньютоновские: суспензии, растворы и расплавы полимеров, коллоидные растворы, консистентные смазки.
Описывается степенными законами: τ = μэф.γ (dυx/dу)n-1 dυx/dу
Основной закон гидростатики
|
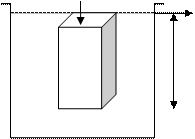
 Определяет распределение давления в покоящейся жидкости, которая всегда действует по нормали к выделенной площадке по направлению внутрь.
Определяет распределение давления в покоящейся жидкости, которая всегда действует по нормали к выделенной площадке по направлению внутрь. 
 P0
P0
 |
|
 ddddddF
ddddddF
dmg = ρg dV
Общая сила, действующая на нижнюю площадку, равна:
dP = PodF + ρg dV
Очевидно, что V столба жидкости равен:
dV = dF Z , тогда давление жидкости на глубине Z, определяется как:
р = dP/dF = Po + ρg Z (*)
Уравнение (*) выражает основной закон гидростатики: давление в любой точке покоящейся жидкости равно сумме внешнего давления на свободной межфазной поверхности и веса столба жидкости над данной точкой. Если разделить все члены уравнения (*) на ρg - удельный вес, то получим:
ρ/ ρg = Ро/ ρg + Z, где
Z-геометрическая высота
Ро/ ρg – пьезометрическая высота.
Пьезометрический напор – высота столбца жидкости, которая создает в данной точке жидкости давление, равное Р. Значит, давление можно измерять в единицах высоты столбца жидкости.
Давление в жидкостях определяется с помощью приборов, называемых манометрами.
|
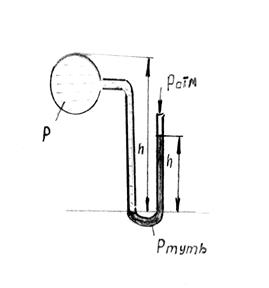 |
Простейшим является U-образная трубка, заполненная ртутью.
Следовательно, на эту величину изменяется давление в любой точке покоящейся жидкости; это уравнение выражает закон Паскаля: давление на поверхность жидкости, покоящееся в состоянии равновесия, передается без изменения величины одинаково по всем направлениям.
P2

|
| |


1, 2 - цилиндры;
3, 4 - поршни (плунжеры);
5 - соединительный канал.
Сила давления, действующая на малый плунжер, создает давление р в жидкости, находящейся в цилиндре 2.
Давление создается торцевой поверхностью плунжера малого диаметра:
р=Р1/F1,
где F1=πd2/4 - площадь поперечного сечения плунжера
Это давление, согласно закону Паскаля, передается на трубке 5 в цилиндр 1 и действует на торец плунжера 3 с помощью поперечного сечения F2=πD2/4.
Сила, с которой плунжер 3 действует на изделие, находится следующим образом:
Р2 = рF2 = P1F2/F1 = P1 *D22/d22
Таким образом, сила прессования в жидкости прямо пропорциональна отношению D2/d2 и может достигать очень высоких значений.
Гидродинамика. Основные понятия
Режимы движения жидкости
Существует два режима течения:
1. Ламинарный
2. Турбулентный
Различные течения можно проследить, если ввести в поток струйку подкрашенной жидкости (англ. ученый Рейнольдс).
Многочисленные опыты показали, что при небольших скоростях жидкости, частицы ее движутся параллельными слоями, не перемешиваясь один с другим. Это ламинарный режим.
При дальнейшем увеличении движения скорости частицы увеличиваются, и частицы начинают двигаться беспорядочно, причем эти направления все время изменяются, т.е. наступает турбулентный режим.
И Рейнольдс установил, что тот или иной режим течения можно охарактеризовать безразмерной зависимостью между скоростью движения жидкости, диаметром трубы, вязкостью и плотностью.
Re=Vdp/M - критерий Рейнольдса
Переход от ламинарного к турбулентному режиму происходит при критическом значении Re, которое равно Reкр = 2320.
Re<Re - ламинарный;
Re>Reкр - турбулентный;
Re>104 - развитый турбулентный режим.
Параметры потоков жидкости
Движение жидкости характеризуется определенными кинематическими и геометрическими переменными величинами и постоянными геометрическими параметрами.
Основная кинематическая величина движения жидкости - ее скорость;
Скорость движения является функцией координат пространства и времени.
Различают два вида движения жидкости: стационарное и нестационарное.
Стационарным называется такое движение жидкости, при котором скорость изменяется только в пространстве, но постоянна во времени.
Нестационарное движение - при котором скорость изменяется в пространстве и во времени.
Нестационарное движение имеет место в периодических процессах, а стационарное - в непрерывных.
Геометрическими характеристиками движения жидкости являются линии тока.
Линия тока - это касательная, проведенная к векторам скорости, соответствующим различным положениям движущейся частицы жидкости в пространстве.
Линией тока будет М1 М4, вдоль которой движутся частицы жидкости при стационарном движении.
U1

 U2
U2
U3
 |
M2 M3 U4

M1 M4
Совокупность линий тока образует элементарную струйку, которая ограничена замкнутой поверхностью.
 U
U

Элементарная струйка
 |
dF
Совокупность элементарных струек образует поток жидкости.

 2 F2 U2
2 F2 U2
|

 1
1 
F 2
Поток жидкости
Одним из геометрических параметров потока жидкости служит площадь живого сечения, т.е. площадь поперечного сечения потока, проведенного нормалью к линиям тока (F1 и F2).
Другой геометрический параметр потока - гидравлический радиус Rr - отношение площади живого сечения потока к его смоченному периметру П, которым является линия соприкосновения живого сечения с твердыми стенками, ограничивающими поток:
Rr=F/П
Для течения в круглой трубе: Rr = d/4,
Rr = вН/(в + 2Н),
где в - ширина канала, Н - высота жидкости.
Для течения жидкости в аппаратах некруглого сечения вводят понятие эквивалентного диаметра:
dэкв = 4Rr = 4F/П,
здесь d - диаметр трубы.
Уравнение неразрывности
Уравнение неразрывности является гидравлической интерпретацией закона сохранения материи.
Введем понятие о расходе жидкости, которым называется количество жидкости, протекающей в единицу времени через данное живое сечение потока.
Различают массовый и объемный расход жидкости.
Массовый расход - это масса жидкости, протекающая в единицу времени:
qm = m/t кг/с.
Объемный расход - объем жидкости, протекающий в единицу времени:
qv = V/t м3/с
Так как m = 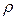 V, то qm =
V, то qm = 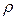 qv.
qv.
Скорость в разных точках живого сечения потока различны по величине, поэтому вводят понятие о средней скорости потока.
Средняя скорость потока - это такая фиктивная, постоянная по всему живому сечению, скорость, при которой через него протекает такой же объемный расход жидкости, как и при реальном распределении скоростей. Средняя скорость равна:
V = qv/F м/с, следовательно qv = VF.
Таким образом, объемный расход несжимаемой жидкости равен произведению средней скорости на площадь живого сечения потока. Согласно закону сохранения массы, количество жидкости, втекающее в сечение 1-1 потока, будет равно количеству жидкости, вытекающему через сечение 2-2, и является величиной постоянной, что можно записать в виде:
| |||
 | |||
 1 2
1 2
 |
F1 2
| |||
 | |||
Это уравнение называется уравнением неразрывности сжимаемой жидкости. Если жидкость несжимаема и 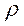 =const, то уравнение неразрывности для несжимаемой жидкости имеет вид: qv = V1F1 = V2F2 = const (2).
=const, то уравнение неразрывности для несжимаемой жидкости имеет вид: qv = V1F1 = V2F2 = const (2).
Объемный расход несжимаемой жидкости есть величина постоянная и равна произведению средней скорости потока на площадь его живого сечения. Из уравнения (2) следует, что V1/V2 = F2/F1, т.е. средние скорости обратно пропорциональны отношению площадей живых сечений потока жидкости.