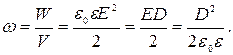Если ввести приведенные величины

, , ,

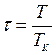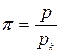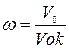то уравнение Ван–дер–Ваальса примет вид (для одного киломоля)

.

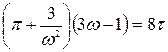Насыщенные пары и жидкости

Абсолютной влажностью называется парциальное давление водяных паров, находящихся в воздухе. Относительной влажностью ω называется отношение абсолютной влажности к парциальному давлению водяных паров, насыщающих пространство при данной температуре.

Удельной теплотой парообразования (испарения) r называется количество тепла, необходимое для превращения единицы массы жидкости в пар при постоянной температуре.

Молекулярная теплота испарения r₀ равна

,

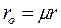где μ – масса одного киломоля.

Зависимость давления насыщенного пара p_н от температуры дается уравнением Клаузиуса – Клапейрона

,

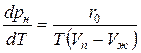где V_п – объем одного киломоля пара и V_ж – объем одного киломоля жидкости.

Относительное изменение объема жидкости при нагревании определяется формулой

,

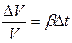где β – коэффициент объемного расширения

Относительное изменение объема жидкости при изменении давления

,

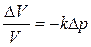где k – коэффициент сжатия.

Коэффициент поверхностного натяжения α численно равен силе, приложенной к единице длины края поверхностной пленки жидкости, т.е.

.

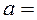
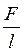При изменении площади пленки на ∆S совершается работа

.

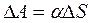Добавочное давление, вызванное кривизной поверхности жидкости, определяется формулой Лапласа

,

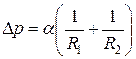где R₁ и R₂ – радиусы кривизны двух взаимно – перпендикулярных сечений поверхности жидкости. Радиус R считается положительным, если центр кривизны находится внутри жидкости (выпуклый мениск) и отрицательным, если центр кривизны находится вне жидкости (вогнутый мениск).

Высота поднятия жидкости в капиллярной трубке

,

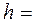
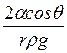где r – радиус трубки, ρ – плотность жидкости и θ – краевой угол.

При полном смачивании θ = 0, при полном не смачивании θ = π.

Давление ненасыщенных паров p₁ над вогнутой поверхностью жидкости меньше, а над выпуклой – больше, чем давление p₀ над плоской поверхностью. Добавочное давление равно

,

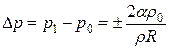где ρ – плотность жидкости , ρ₀ – плотность ненасыщенных паров жидкости и R – радиус кривизны поверхности жидкости.

Осмотическое давление P раствора связано с его абсолютной температурой T формулой Вант – Гоффа

.

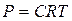Здесь R – газовая постоянная и 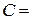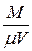- число киломолей растворенного вещества в единице объема раствора (молярная концентрация раствора).

Для растворов недиссоциированных молекул вещества

,

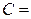
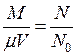где N₀ – число Авогадро и N – число молекул растворенного вещества в единице объема.

При наличии диссоциации число частиц в единице объема будет больше, что приведет к увеличению осмотического давления.

Давление насыщенных паров над раствором меньше, чем над чистым растворителем. При достаточно малой концентрации раствора относительное уменьшение давления насыщенного пара над раствором определяется законом Рауля

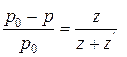
где p₀ – давление насыщенного пара над чистым растворителем, p – давление насыщенного пара над раствором, z^' – число киломолей растворенного вещества и z – число киломолей жидкости.

Твердые тела.

Изменение температуры плавления dT при изменении давления на dp дается уравнением Клаузиуса – Клапейрона

,

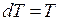
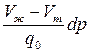где q₀ – молекулярная теплота плавления, V_ж – объем одного киломоля жидкости , V_т – объем одного киломоля твердого тела и T – температура плавления.

При не очень низких температурах для твердых тел имеет место закон Дюлонга и Пти, согласно которому атомная теплоемкость всех химически простых твердых тел равна приблизительно 3R = 25 ∙10³ дж /кг·моль·К = 6 кал /г·моль·К.

Количество тепла, переносимого вследствие теплопроводности за время ∆t. определяется формулой

,

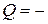
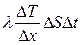где 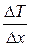- градиент температуры в направлении, перпендикулярном площадке ∆S, λ – коэффициент теплопроводности.

При повышении температуры длина твердых тел возрастает в первом приближении линейно с температурой, т.е.

,

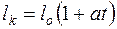где l_t – длина тела при температуре t, l₀ – его длина при температуре 0°С и а – коэффициент линейного теплового расширения.

Для твердых изотропных тел 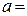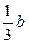, где b – коэффициент объемного теплового расширения.

В случае деформации продольного растяжения (или одностороннего сжатия) стержня относительное изменение длины стержня по закону Гука

,

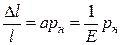где p_н – удельная нагрузка, т.е. 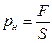, где F – растягивающая (сжимающая) сила, S – площадь поперечного сечения и α – коэффициент упругости. Величина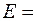 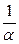называется модулем упругости (модулем Юнга).

Относительное изменение толщины стержня при продольном растяжении

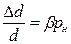
где β – коэффициент поперечного сжатия. Величина

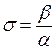
называется коэффициентом Пуассона.

Для закручивания стержня (проволоки) на некоторый угол φ необходимо приложить момент пары сил

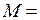
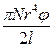
где l – длина проволоки , r – ее радиус и N - модуль сдвига материала проволоки.

Электродинамика

Электростатика

Электрическое поле –это особая форма существования материи, связанная с электрическими зарядами и осуществляющая взаимодействие между заряженными телами. Электрический заряд является физической величиной, определяющей интенсивность электромагнитных взаимодействий.

Суммарный заряд электрически изолированной системы не изменяется (закон сохранения электрического заряда). Электрические заряды не создаются и не исчезают, они лишь передаются от одного тела к другому или перераспределяются внутри данного тела.

Раздел электродинамики, в котором изучается взаимодействие неподвижных электрических зарядов, называется электростатикой. Такое взаимодействие осуществляется посредством электростатического поля.

Неподвижные точечные электрические заряды взаимодействуют в вакууме с силой, определяемой законом Кулона:

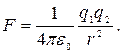
Силовой характеристикой электростатического поля является напряженность. Она численно равна силе, действующей со стороны поля на единичный положительный заряд, помещенный в данную точку поля:

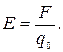
Напряженности полей, создаваемых отдельными зарядами, складываются геометрически (принцип суперпозиции):

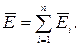
Электростатическое поле является потенциальным, т.е. работа, совершаемая при перемещении заряда, не зависит от траектории, а определяется лишь начальным и конечным положениями заряда. Эта работа численно равна изменению потенциальной энергии:

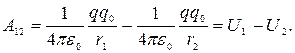
Энергетической характеристикой поля является потенциал. Он характеризует потенциальную энергию, которой обладал бы единичный положительный заряд, помещенный в данную точку поля:

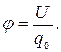
Потенциал в какой-либо точке электрического поля, образованного системой зарядов, равен алгебраической сумме потенциалов, создаваемых каждым зарядом системы:

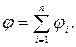
Разность потенциалов – это скалярная физическая величина, определяемая работой, совершаемой кулоновскими силами при перемещении единичного положительного заряда из одной точки поля в другую:

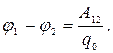
Силовая и энергетическая характеристики поля связаны между собой соотношением

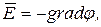
т.е. напряженность поля равна градиенту потенциала со знаком «минус». Это означает, что вектор напряженности электростатического поля направлен в сторону убывания потенциала. В случае однородного поля (например, поля плоского конденсатора) модуль напряженности определяется по формуле

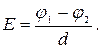
Вычисление напряженности поля большой системы электрических зарядов с помощью принципа суперпозиции электростатических полей можно упростить, используя теорему Гаусса:

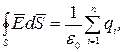
т.е. поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на электрическую постоянную.

При внесении диэлектрика во внешнее электрическое поле происходит его поляризация. Поляризованный диэлектрик создает собственное поле, которое внутри диэлектрика ослабляет внешнее электрическое поле в 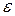раз:

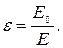
Теорема Гаусса для электростатического поля в диэлектрике формулируется следующим образом: поток вектора смещения электростатического поля в диэлектрике сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности свободных электрических зарядов, т.е.

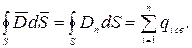
Способность проводника накапливать электрические заряды характеризуется электрической емкостью:

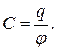
Электрическая емкость не зависит от заряда проводника, а определяется его геометрическими размерами и формой, расположением относительно других проводников и электрическими свойствами окружающей среды.

Емкостью конденсатора называется физическая величина, равная отношению заряда 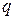, накопленного в конденсаторе, к разности потенциалов между его обкладками:

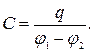
Электрическая емкость плоского конденсатора

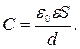
Заряженный конденсатор обладает энергией

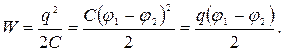
Энергия конденсатора сосредоточена в электрическом поле. Объемная плотность энергии электростатического поля определяется следующим образом: