Средняя длина свободного пробега молекул газа

,

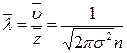где 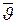- средняя арифметическая скорость, 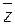- среднее число столкновений каждой молекулы с остальными в единицу времени, σ – эффективный диаметр молекулы и n – число молекул в единице объема.

Общее число столкновений всех молекул в единице объема за единицу времени равно

.

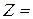
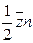Масса М, перенесенная за время ∆t при диффузии, определяется уравнением

,

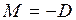
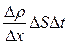где 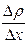- градиент плотности в направлении, перпендикулярном к площадке ∆S и D – коэффициент диффузии, равный

.

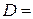
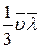Здесь 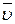- средняя скорость, 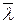- средняя длина свободного пробега молекул.

Количество движения, перенесенное газом за время ∆t, определяет силу внутреннего трения F в газе:

,

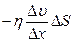где 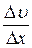- градиент скорости течения газа в направлении, перпендикулярном к площадке ∆S,а η – коэффициент внутреннего трения (динамическая вязкость)

.

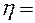
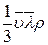Количество тепла Q , перенесенное за время ∆t в результате теплопроводности, равно

,

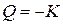
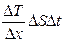где 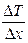- градиент температуры в направлении, перпендикулярном к площадке ∆S, К – коэффициент теплопроводности, равный

.

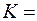
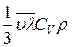Первое начало термодинамики может быть записано в виде

,

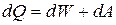где dQ – количество тепла, полученного газом; dW – изменение внутренней энергии газа и dA=pdV – работа, совершаемая газом при изменении его объема. Изменение внутренней энергии газа

,

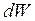
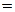
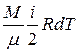где dT – изменение температуры.

Полная работа при изменении объема газа

.

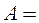
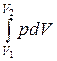Работа, совершаемая при изотермическом изменении объема газа,

.

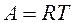
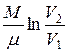Давление газа и его объема связаны при адиабатическом процессе уравнением Пуассона

т.е. ,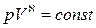

где показатель адиабаты .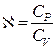

Уравнение Пуассона может быть записано еще в таком виде

,

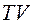
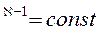т.е.

,

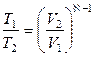или ,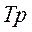

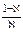
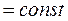т.е.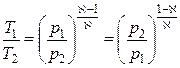

Работа, совершаемая при адиабатическом изменении объема газа, может быть найдена по формуле

.

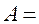
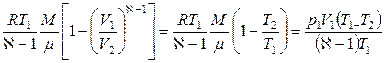Где p₁ и V₁ давление и объем газа при температуре T₁.

Уравнение политропического процесса имеет вид:

,

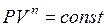или ,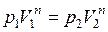

где n – показатель политропы (1 ‹ n ‹ ).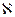

Коэффициент полезного действия тепловой машины

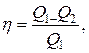
где Q₁ – тепло, переданное рабочему телу, и Q₂ – тепло, отданное холодильнику. Для идеального цикла Карно

,

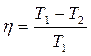где T₁ – температура нагревателя , T₂ – температура холодильника.

Разность энтропий 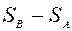двух состояний В и А определяется формулой

.

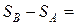
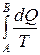Реальные газы.

Уравнение состояния реальных газов (уравнение Ван–дер– Ваальса) для одного киломоля имеет вид:

,

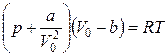где V₀ – объем одного киломоля газа, а и b – постоянные, различные для разных газов, p – давление, T – абсолютная температура и R – газовая постоянная.

Уравнение Ван–дер–Ваальса, отнесенное к любой массе М газа, имеет вид:

,

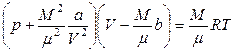где V – объем всего газа, µ - масса одного киломоля.

В этом уравнении 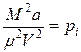- давление, обусловленное силами взаимодействия молекул, и 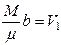- объем, связанный с собственным объемом молекул.

Постоянные а и b данного газа связаны с его критической температурой T_к, критическим давлением p_k и критическим молярным объемом V_0k следующими соотношениями:

, , .

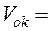
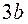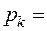
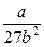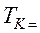
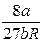Эти уравнения можно решить относительно постоянных а и b:

, .
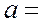
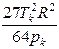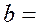
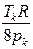