Изучение законов внешнего фотоэффекта
И определение постоянной Планка
Цель работы: изучение законов внешнего фотоэффекта; исследование вольтамперных характеристик вакуумного фотоэлемента; определение работы выхода и определение постоянной Планка.
Принадлежности: осветитель типа ОТП; вакуумный фотоэлемент СЦВ-4; стеклянные светофильтры (3 шт.); источник напряжения ВУП-2; два цифровых вольтметра В7-27; оптическая скамья.
ТЕОРИЯ
Явление вырывания электронов из металла под действием света называется внешним фотоэффектом. Это явление было открыто в 1887 году Г.Герцем и детально исследовано русским физиком А.Г.Столетовым (1888 год), а также В.Хальваксом, А.Риги и др. Фотоэлектроны при движении во внешнем электрическом поле создают фототок. Фотоэффект сыграл важную роль в создании квантовой теории света и широко применяется в технике (системы записи звука, автоматика и телемеханика, телевидение и др.).
Основные законы внешнего фотоэффекта заключаются в следующем:
1. Фототок насыщения прямо пропорционален световому потоку (закон Столетова):
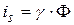 , (1)
, (1)
где 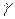 - интегральная чувствительность фотокатода (если используется белый, немонохроматический свет), или спектральная чувствительность (если используется монохроматический свет).
- интегральная чувствительность фотокатода (если используется белый, немонохроматический свет), или спектральная чувствительность (если используется монохроматический свет).
2. Скорость (а, следовательно, и кинетическая энергия) фотоэлектронов не зависит от интенсивности света, а зависит только от его частоты (опыты Ф.Ленарда и др.).
3. Фотоэффект наблюдается только при достаточно высокой частоте 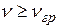 . Частота
. Частота 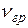 различна для разных металлов и называется красной границей фотоэффекта.
различна для разных металлов и называется красной границей фотоэффекта.
4. Фотоэффект практически безинерционен (при включении света фототок появляется через время порядка 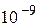 с, т.е. практически мгновенно).
с, т.е. практически мгновенно).
Теория фотоэффекта, объяснившая указанные закономерности, была разработана в 1905 году А.Эйнштейном, предположившим, что свет не только излучается и поглощается, но и распространяется порциями – квантами. Таким образом, свет обнаруживает в теории фотоэффекта корпускулярные (квантовые) свойства и ведет себя как поток частиц – фотонов. Энергия и импульс фотона соответственно равны
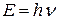 ,
, 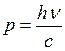 ,
,
Коэффициент пропорциональности h между энергией Е и частотой 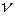 называется постоянной Планка. Постоянная Планка может входить во многие физические соотношения, в связи с чем может быть определена различными способами. Определенное из опыта значение равно
называется постоянной Планка. Постоянная Планка может входить во многие физические соотношения, в связи с чем может быть определена различными способами. Определенное из опыта значение равно
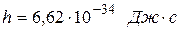 .
.
Согласно теории Эйнштейна, энергия, полученная электроном, доставляется ему в виде кванта 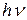 , которая усваивается им целиком. Часть этой энергии, равная работе выхода, затрачивается на то, чтобы электрон мог покинуть металл. Если электрон освобождается светом не у самой поверхности, а на некоторой глубине, то часть энергии, равная
, которая усваивается им целиком. Часть этой энергии, равная работе выхода, затрачивается на то, чтобы электрон мог покинуть металл. Если электрон освобождается светом не у самой поверхности, а на некоторой глубине, то часть энергии, равная 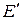 , может быть потеряна вследствие случайных столкновений в веществе. Остаток энергии образует кинетическую энергию
, может быть потеряна вследствие случайных столкновений в веществе. Остаток энергии образует кинетическую энергию 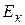 электрона, покинувшего вещество. Энергия
электрона, покинувшего вещество. Энергия 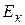 будет максимальна, если
будет максимальна, если 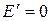 . В этом случае выполняется соотношение
. В этом случае выполняется соотношение
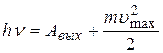 , (2)
, (2)
которое называется уравнением Эйнштейна.
Из уравнения (2) вытекают законы внешнего фотоэффекта.
По Эйнштейну величина светового потока пропорциональна числу фотонов, а число выбитых электронов равно числу падающих на поверхность металла фотонов. Отсюда и вытекает закон Столетова.
Второй закон фотоэффекта непосредственно вытекает из уравнения (2). Действительно, согласно уравнению Эйнштейна, кинетическая энергия фотоэлектронов 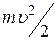 зависит только от частоты света
зависит только от частоты света 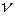 , т.к. работа выхода для данного металла есть величина постоянная.
, т.к. работа выхода для данного металла есть величина постоянная.
Существование граничной частоты 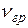 также есть очевидное следствие уравнения (2): при уменьшении частоты света энергия фотоэлектронов уменьшается и при некоторой частоте
также есть очевидное следствие уравнения (2): при уменьшении частоты света энергия фотоэлектронов уменьшается и при некоторой частоте 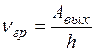 обращается в нуль.
обращается в нуль.
Безынерционность фотоэффекта объясняется квантовым характером взаимодействия света с веществом.
Уравнение (2) было проверено в США Р.Милликеном (1916 г.), а также в Советском Союзе П.И.Лукирским и С.С.Прилежаевым (1928 г.), которые создали прибор в виде сферического конденсатора. Анодом в их приборе служили серебряные стенки стеклянного сферического баллона. В центре баллона помещался катод в виде шарика. Суть опытов состояла в определении кинетической энергии фотоэлектронов методом задерживающего потенциала. Электроны, вылетающие из катода фотоэлемента под действием света, обладают определенной кинетической энергией и достигают анода, создавая в замкнутой цепи, составленной из фотоэлемента и гальванометра, ток. Если между анодом и катодом создать электростатическое поле, приложив разность потенциалов, то можно затормозить электроны. При некотором значении разности потенциалов даже самые быстрые электроны не будут достигать анода, ток в цепи отсутствует. Условие этого
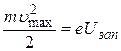 .
.
Величина U называется задерживающей разностью потенциалов. Тогда, из уравнения (2) следует, что
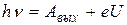 . (3)
. (3)
Из формулы (3) следует, что U зависит от частоты света, падающего на фотоэлемент. Поэтому, если измерить зависимость задерживающей разности потенциалов U от частоты 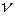
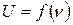 ,
,
то из графика этой зависимости можно определить постоянную Планка и работу выхода электрона. Уравнение (3) можно переписать в виде уравнения прямой
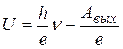 .
.
 Величина
Величина 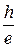 равна тангенсу угла наклона этой прямой, а
равна тангенсу угла наклона этой прямой, а 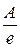 - отрезку на оси U, отсекаемому прямой от начала координат (рис. 1).
- отрезку на оси U, отсекаемому прямой от начала координат (рис. 1).
В качестве фотоэлемента в работе применяется серийный вакуумный фотоэлемент СЦВ-4. Он выполнен в виде стеклянного баллона, воздух из которого откачан до давления 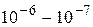 мм.рт.ст. На одну половину внутренней поверхности баллона на подкладочный слой магния или серебра нанесен тонкий слой сурьмы, а затем тонкий слой цезия. Образующееся при этом соединение
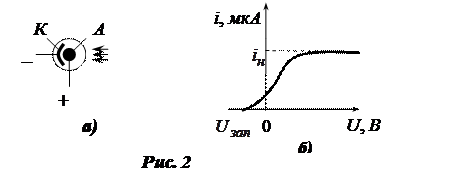
мм.рт.ст. На одну половину внутренней поверхности баллона на подкладочный слой магния или серебра нанесен тонкий слой сурьмы, а затем тонкий слой цезия. Образующееся при этом соединение 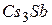 служит катодом. Такой катод обладает малой работой выхода и, следовательно, красная граница фотоэффекта для данного фотоэлемента находится в видимой части спектра. В центральной части баллона расположен металлический анод А, имеющий форму сферы (рис. 2, а). Если на катод К направить пучок света и создать между анодом и катодом разность потенциалов, то ускоряемые электрическим полем электроны летят к аноду и обусловливают прохождение тока. Получаемый ток зависит от освещенности, фототок растет с напряжением, но при определенном напряжении достигает насыщения и дальнейшее повышение напряжения уже не приводит к увеличению тока. Зависимость фототока от напряжения выражают кривой, называемой вольтамперной характеристикой фотоэлемента (рис. 2, б). При постоянном напряжении величина фототока пропорциональна потоку световой энергии
служит катодом. Такой катод обладает малой работой выхода и, следовательно, красная граница фотоэффекта для данного фотоэлемента находится в видимой части спектра. В центральной части баллона расположен металлический анод А, имеющий форму сферы (рис. 2, а). Если на катод К направить пучок света и создать между анодом и катодом разность потенциалов, то ускоряемые электрическим полем электроны летят к аноду и обусловливают прохождение тока. Получаемый ток зависит от освещенности, фототок растет с напряжением, но при определенном напряжении достигает насыщения и дальнейшее повышение напряжения уже не приводит к увеличению тока. Зависимость фототока от напряжения выражают кривой, называемой вольтамперной характеристикой фотоэлемента (рис. 2, б). При постоянном напряжении величина фототока пропорциональна потоку световой энергии 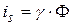 , где
, где 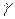 - интегральная чувствительность фотоэлемента – величина фототока, отнесенная к одному люмену потока световой энергии. Величина
- интегральная чувствительность фотоэлемента – величина фототока, отнесенная к одному люмену потока световой энергии. Величина 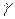 для различных вакуумных фотоэлементов имеет значение от нескольких микроампер на люмен до 100
для различных вакуумных фотоэлементов имеет значение от нескольких микроампер на люмен до 100 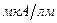 .
.
 Если считать лампу точечным источником света, то зависимость освещенности от расстояния описывается известной формулой:
Если считать лампу точечным источником света, то зависимость освещенности от расстояния описывается известной формулой:
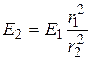 ,
,
где 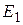 и
и 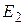 - освещенности, соответствующие расстояниям
- освещенности, соответствующие расстояниям 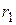 и
и 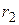 до источника света. Если, в частности,
до источника света. Если, в частности, 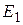 - минимальная освещенность на максимальном расстоянии
- минимальная освещенность на максимальном расстоянии 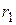 (длина оптической скамьи), то отношение
(длина оптической скамьи), то отношение 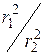 пропорционально освещенности фотокатода. Это отношение представляет собой, таким образом, относительную освещенность фотокатода.
пропорционально освещенности фотокатода. Это отношение представляет собой, таким образом, относительную освещенность фотокатода.
Порядок выполнения работы
1. Зависимость фототока от освещенности фотокатода.
1. Соберите схему, изображенную на рис.3. Установите рукоятку регулировки напряжения источника ВУП-2 в среднее положение, при котором напряжение на выходе 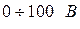 равно нулю.
равно нулю.
2. 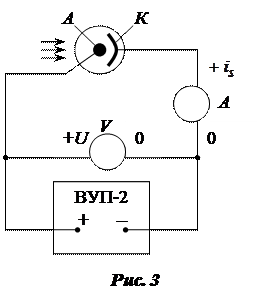 Поместите лампу осветителя на расстояние 15 см от фотоэлемента и включите приборы. Установите на фотоэлементе напряжение насыщения и запишите в таблицу 1 величину фототока. Удалив лампу на 5 см, запишите новое значение фототока и т.д. до конца оптической скамьи. Затем возвратите лампу осветителя в исходное положение через те же промежуточные этапы, отмечая каждый раз величину фототока. При измерениях следите, чтобы напряжение на фотоэлементе оставалось неизменным.
Поместите лампу осветителя на расстояние 15 см от фотоэлемента и включите приборы. Установите на фотоэлементе напряжение насыщения и запишите в таблицу 1 величину фототока. Удалив лампу на 5 см, запишите новое значение фототока и т.д. до конца оптической скамьи. Затем возвратите лампу осветителя в исходное положение через те же промежуточные этапы, отмечая каждый раз величину фототока. При измерениях следите, чтобы напряжение на фотоэлементе оставалось неизменным.
Таблица 1
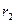 , см , см | ||||||||
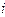 , мкА , мкА 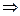 | ||||||||
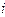 , мкА , мкА 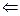 | ||||||||
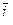 , мкА , мкА |
Примечание: измерения можно проводить в белом свете или со светофильтром (по указанию преподавателя).
2. Вольтамперная характеристика вакуумного фотоэлемента
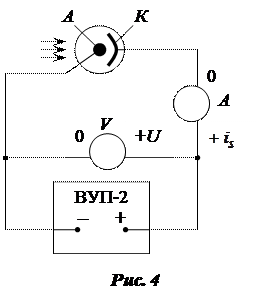
1. Экспериментальная схема такая же, как и в п.1. Поместите лампу на расстояние 15 см от фотоэлемента. Снимите зависимость 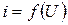 (U – напряжение на фотоэлементе). Напряжение изменять от нуля до насыщения. Показания записать в таблицы 2.
(U – напряжение на фотоэлементе). Напряжение изменять от нуля до насыщения. Показания записать в таблицы 2.
2. Те же измерения проведите, поместив лампу на расстояния 25 см и 35 см. Измерения запишите в таблицу 2.
3. Уменьшите питающее напряжение до нуля.
Таблица 2
| r, см | 1. | … | ||
| 15 см | i, мкА | |||
| u, В | ||||
| 25 см | i, мкА | |||
| u, В | ||||
| 35 см | i, мкА | |||
| u, В |
Примечание: Измерения можно проводить с одним из светофильтров.
3. Определение Постоянной Планка и работы выхода.
1. Соберите схему, изображенную на рис. 4.
2. В осветитель вставьте один из прилагаемых светофильтров.
3.  Увеличивайте по абсолютной величине отрицательное напряжение на выходе источника ВУП-2 и наблюдайте за уменьшением тока. Отметьте напряжение, при котором фототок обращается в нуль. Это и есть запирающее напряжение
Увеличивайте по абсолютной величине отрицательное напряжение на выходе источника ВУП-2 и наблюдайте за уменьшением тока. Отметьте напряжение, при котором фототок обращается в нуль. Это и есть запирающее напряжение 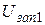 . Результаты запишите в таблицу 3.
. Результаты запишите в таблицу 3.
4. Уменьшите напряжение до нуля.
5. Те же измерения повторите со вторым и третьим светофильтрами и определите соответствующие напряжения 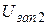 и
и 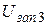 . Результаты запишите в таблицу 3.
. Результаты запишите в таблицу 3.
Таблица 3
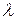 , нм , нм | 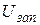 , В , В |
| 1. 2. 3. |
Обработка результатов
1. По данным таблицы 1 постройте зависимость 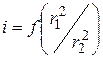 . Сделайте вывод.
. Сделайте вывод.
2. По данным таблицы 2 постройте графики. Сделайте вывод.
3. По данным таблицы 3 постройте зависимость 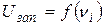 , где
, где 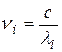 - частота света, прошедшего i-й светофильтр. (
- частота света, прошедшего i-й светофильтр. ( 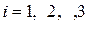 ),
), 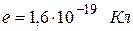 - заряд электрона.
- заряд электрона.
4. Проведите через полученные точки прямую. Продолжив эту прямую до пересечения с осями координат, определите постоянную Планка h ( 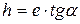 , где
, где 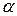 - угол наклона прямой к оси абсцисс) и работу выхода в электронвольтах (
- угол наклона прямой к оси абсцисс) и работу выхода в электронвольтах ( 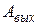 равна отрезку, отсекаемому прямой по оси ординат). Результаты запишите в таблицу 6.
равна отрезку, отсекаемому прямой по оси ординат). Результаты запишите в таблицу 6.
Таблица 4
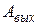 , эВ , эВ | h, 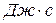 |
Контрольные вопросы
1. Назовите различные виды фотоэффекта.
2. В чем заключается явление внешнего фотоэффекта?
3. Сформулируйте основные законы внешнего фотоэффекта.
4. В чем заключается теория Эйнштейна для фотоэффекта?
5. Запишите уравнение Эйнштейна. Объясните его физический смысл?
6. Что называется работой выхода?
7. Чему равны энергия и импульс фотона?
8. Что называется постоянной Планка? Чему она равна?
9. Дайте объяснение законам фотоэффекта с точки зрения теории Эйнштейна.
10. В чем заключаются опыты Милликена, Лукирского и Прилежаева по определению постоянной Планка и работы выхода?
11. Как определить работу выхода, если известны задерживающие разности потенциалов для двух частот?
12. Устройство и принцип работы фотоэлемента.
Литература
1. А.А.Детлаф, Б.М.Яворский, Курс физики, т. 3, М., «Высшая школа», 1979.
2. И.В.Савельев Курс общей физики, т. 3, М., «Астрель», 2005.
Лабораторная работа 2.06
Изучение излучения нити лампы накаливания и определение постоянной Планка
Цель работы: определение постоянной Стефана-Больцмана, определение постоянной Планка, ознакомление с принципом действия оптического пирометра.
Принадлежности: оптический пирометр ОППИР-017; лампа накаливания; аккумулятор; амперметр; вольтметр; регулируемый источник постоянного тока.
ТЕОРИЯ
При любой температуре все тела излучают электромагнитные волны различной длины. Излучение нагретых тел называется тепловым. Если температура Т порядка комнатной и ниже, то большая часть энергии излучается в инфракрасной части спектра. И лишь при 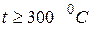 тело начинает светиться. Тепловое излучение – единственное излучение, которое находится в термодинамическом равновесии с излучающим телом, т.е. когда излучаемая в единицу времени энергия равна поглощаемой за то же время. Причиной термодинамического равновесия является то, что интенсивность теплового излучения пропорциональна температуре.
тело начинает светиться. Тепловое излучение – единственное излучение, которое находится в термодинамическом равновесии с излучающим телом, т.е. когда излучаемая в единицу времени энергия равна поглощаемой за то же время. Причиной термодинамического равновесия является то, что интенсивность теплового излучения пропорциональна температуре.
Энергия испускается атомами в виде отдельных порций (квантов), которые ведут себя подобно потоку частиц – фотонов. Энергия и импульс фотона равны:
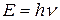 ,
, 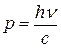 , (1)
, (1)
Коэффициент пропорциональности h между энергией Е и частотой 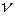 называется постоянной Планка. Постоянная Планка может входить во многие физические соотношения, в связи с чем может быть определена различными способами. Определенное из опыта значение равно
называется постоянной Планка. Постоянная Планка может входить во многие физические соотношения, в связи с чем может быть определена различными способами. Определенное из опыта значение равно
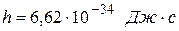 .
.
Вся квантовая оптика основана на уравнениях (1). Таким образом, можно сказать, что нагретое тело излучает электромагнитные волны, а можно сказать, что оно испускает фотоны.
Попавший на поверхность тела фотон будет либо отражен, либо поглощен, либо пропущен ею. Если фотон будет поглощен, то температура тела и внутренняя энергия возрастут.
Тело, поглощающее всю падающую на него энергию, называется абсолютно черным. В природе не существует тел, совпадающих по своим свойствам с абсолютно черными. Тела, покрытые сажей или платиновой чернью, приближаются по своим свойствам к абсолютно черным лишь в ограниченном интервале длин волн. Черная поверхность может, например, хорошо поглощать видимый свет, но в то же время хорошо отражать инфракрасные лучи. И наоборот, некоторые светлые (для видимого света!) материалы (бетон, фарфор, фаянс, кирпич) очень хорошо поглощают инфракрасные лучи.
Тело может излучать электромагнитные волны не только потому, что оно нагрето. Причиной излучения может быть химическая реакция (например, окисление фосфора), разряд в газе, бомбардировка поверхности твердого тела электронами или облучение светом. Свечение, возникающее во всех этих случаях, называют люминесценцией.
Обозначим 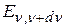 энергию, излучаемую единицей поверхности черного тела в 1 секунду в интервале частот от
энергию, излучаемую единицей поверхности черного тела в 1 секунду в интервале частот от 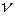 до
до 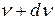 . Тогда
. Тогда
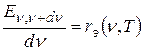 -
-
спектральная излучательная способность тела. Вместо частоты можно рассматривать длину волны света 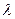 :
:
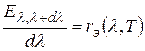 .
.
Проинтегрировав по всем частотам (длинам волн) от 0 до 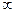 , получим величину, называемую излучательностью:
, получим величину, называемую излучательностью:
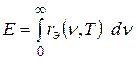 .
.
Излучательность равна энергии, излучаемой в 1 с единицей поверхности черного тела на всех частотах.
Закон Стефана–Больцмана утверждает, что излучательность черного тела пропорциональна четвертой степени абсолютной температуры:
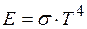 , (2)
, (2)
где 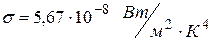 - постоянная Стефана-Больцмана.
- постоянная Стефана-Больцмана.
Распределение энергии в спектре черного тела описывается формулой излучения Планка:
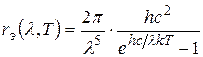 . (3)
. (3)
Интегрируя последнюю функцию по длине волны в пределах от 0 до 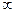 , можно получить закон Стефана-Больцмана и значение постоянной
, можно получить закон Стефана-Больцмана и значение постоянной 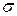 . Расчет приводит к формуле:
. Расчет приводит к формуле:
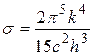 , (4)
, (4)
где 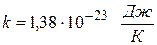 - постоянная Больцмана;
- постоянная Больцмана;
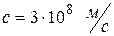 - скорость света в вакууме.
- скорость света в вакууме.
Исследуя функцию (3) на экстремум, можно найти длину волны 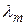 , при которой спектральная плотность излучательности максимальна:
, при которой спектральная плотность излучательности максимальна:
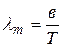 , (5)
, (5)
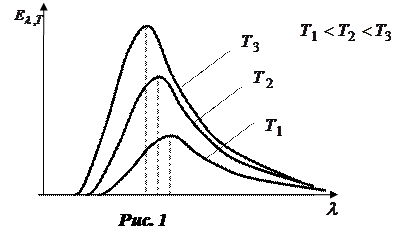
где в – некоторая постоянная, называемая постоянной Вина. Таким образом, чем выше температура Т, тем короче длина волны 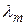 , т.е. максимум кривой распределения смещается с ростом температуры в область все более коротких волн (рис. 1). Выражение (5) носит название закона смещения Вина.
, т.е. максимум кривой распределения смещается с ростом температуры в область все более коротких волн (рис. 1). Выражение (5) носит название закона смещения Вина.

Тепловое излучение нечерных тел описывается интегральным законом Кирхгофа:
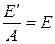 . (6)
. (6)
Здесь Е – излучательность нечерного тела;
А – коэффициент поглощения.
Т.е. отношение излучательности любого тела к коэффициенту поглощения есть величина постоянная для данной температуры и равная излучательности черного тела. Смысл закона состоит в том, что чем лучше тело поглощает (чем больше А), тем лучше оно излучает (тем больше Е).
Из (2) и (6) следует закон Стефана-Больцмана для нечерных тел:
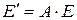
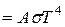 . (7)
. (7)
Коэффициент поглощения А сам зависит от температуры, поэтому зависимость излучательности от температуры для нечерных тел получается более сильной: 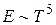 , а при более высоких температурах
, а при более высоких температурах 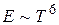 . Для технических целей часто можно положить
. Для технических целей часто можно положить 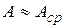 , т.е. считать нечерное тело серым. Это оправдано, если не требуется большая точность, и температура изменяется в узких пределах. В этом случае можно считать, что закон Стефана-Больцмана выполняется и для нечерного тела.
, т.е. считать нечерное тело серым. Это оправдано, если не требуется большая точность, и температура изменяется в узких пределах. В этом случае можно считать, что закон Стефана-Больцмана выполняется и для нечерного тела.
В данной работе источником излучения является нить накала лампы накаливания. Полная мощность излучения нити, с учетом (7), равна:
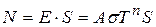 , (8)
, (8)
где S – площадь излучающей поверхности.
Если при температурах 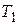 и
и 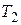 мощности излучения соответственно равны
мощности излучения соответственно равны 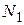 и
и 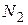 , то из (8) следует, что
, то из (8) следует, что
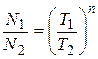 и
и 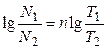 .
.
Отсюда
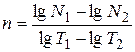 . (9)
. (9)
Как видим, зависимость 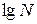 от
от 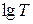 линейна и п есть тангенс угла наклона прямой к оси абсцисс. Построив эту зависимость на графике и определив п, можно решить вопрос о применимости закона Стефана-Больцмана к излучению нити (в этом случае окажется, что
линейна и п есть тангенс угла наклона прямой к оси абсцисс. Построив эту зависимость на графике и определив п, можно решить вопрос о применимости закона Стефана-Больцмана к излучению нити (в этом случае окажется, что 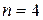 ).
).
Из (8) выразим постоянную Стефана-Больцмана:
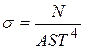 . (10)
. (10)
Из (4) выразим постоянную Планка:
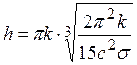 . (11)
. (11)
