Измерение теплопроводности газа

Цель работы: исследовать температурную зависимость коэффициента теплопроводности воздуха.

Принадлежности: цифровой вольтметр В7-27, стрелочный вольтметр, источник питания ВС-24М, «стенд» с исследуемым образцом.

ТЕОРИЯ

Явление теплопроводности представляет собой процесс переноса тепла, обусловленный беспорядочным движением молекул. Если размеры тел, в которых рассматривается перенос тепла, значительно превосходят длины свободного пробега молекул, можно рассматривать вещество как сплошную среду. Тогда основным понятием теории теплопроводности становится температурное поле – совокупность мгновенных значений температур во всех точках среды

.

Если температурное поле зависит и от координат и от времени , то оно называется нестационарным. Температурное поле, не изменяющееся во времени и зависящее, следовательно, только от координат, называется стационарным:

.

В простейшем случае, когда температурное поле зависит только от одной координаты, оно называется одномерным:

.

Точки тела, имеющие одинаковые температуры, образуют изотермические поверхности. Так как одна и та же точка тела не может одновременно иметь различные температуры, изотермические поверхности не могут пересекаться. Они либо оканчиваются на поверхности теплопроводящего тела, либо замыкаются внутри него. В простейших одномерных полях изотермические поверхности представляют собой параллельные плоскости, коаксиальные цилиндрические поверхности с общим центром.

Важной характеристикой поля является градиент. Градиент температуры определяется как вектор, направленный по нормали (перпендикулярно) к изотермической поверхности в сторону возрастания температуры и численно равный изменению температуры на единице расстояния между изотермическими поверхностями. Для поля, изотермическими поверхностями которого являются цилиндры:

. (1)

Градиент температуры измеряется в .

Для переноса тепла в любом веществе необходимо и достаточно существования в нем отличного от нуля градиента температур. При этом между изотермическими поверхностями возникает тепловой поток. Для его характеристики вводится понятие плотности теплового потока q, которая представляет собой количество тепла, протекающего через единицу площади изотермической поверхности в единицу времени:

. (2)

Так как тепло передается от более горячих частей тела к холодным, плотность теплового потока есть величина векторная, направленная противоположно вектору градиента температуры.

Опытный закон Фурье утверждает, что плотность теплового потока пропорциональна градиенту температуры:

. (3)

Коэффициент 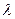называется коэффициентом теплопроводности. В системе СИ он измеряется в . Если процесс переноса тепла стационарен, а между изотермическими поверхностями нет источников или стоков тепла, полный тепловой поток через такие поверхности должен быть одинаков.

Одним из таких методов измерения коэффициента теплопроводности газов является метод нагретой нити. В этом методе исследуемый газ находится в цилиндрической трубке, по оси которой натянута проволока из платины, никеля или другого металла, служащая одновременно источником тепла. Наружная поверхность трубки поддерживается при постоянной температуре, а через проволоку пропускается электрический ток, в результате чего проволока нагревается. Разность температур проволоки и стенок трубки и приводит к возникновению теплового потока. Динамическое равновесное состояние установится, когда выделяемое при прохождении электрического тока тепло будет равно количеству тепла, уносимого за счет теплопроводности. Если принять, что тепло идет от проволоки через газ только по радиусу, то изотермическими поверхностями в газе будут цилиндрические поверхности с общей осью – осью проволоки. Равновесие установится, когда величина мощности будет равна потоку тепла, уходящего за счет теплопроводности и условие равновесия будет соответствовать равенству:

, (4)

где q – плотность теплового потока, соответствующего уравнению (3). Подставляя (3) в (4), получаем

, (5)

Выражение (5) представляет собой дифференциальное уравнение с разделяемыми переменными:

. (6)

Интегрируя (6), получаем:

. (7)

В уравнении (7) содержатся две неизвестные: постоянная интегрирования С и коэффициент теплопроводности 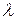. Для их вычисления используем следующие граничные условия:

при , при . (8)

Здесь и - температуры слоев газа, непосредственно прилегающих к поверхностям проволоки и трубки с соответствующими радиусами и . После простых выкладок получим формулу для расчета коэффициента теплопроводности:

. (9)

Для определения 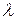необходимо измерить температуры и , которые отождествляются с температурами поверхностей нити и трубки, а также мощность нагревателя и геометрические размеры , , L, которые в нашей лаборатории задаются студенту.

При реализации такого метода возникает ряд источников систематических погрешностей, с которыми необходимо считаться при постановке измерений и обработке их результатов. Рассмотрим важнейшие из них.