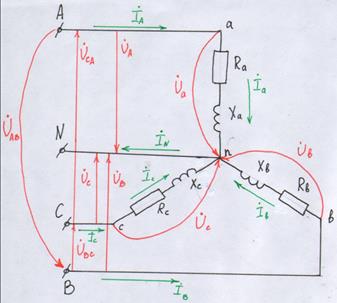
Соединение фаз генератора и нагрузки треугольником.

Для катушек с ферромагнитным сердечником ток, протекающий по катушке является не синусоидальным. Раскладывая этот ток на составляющие гармонически в соответствии с рядом Фурье.

При соединении обмотки генератора по схеме треугольник в режиме холостого хода результирующий ток замыкается по фазам генератора и создаёт на них потери мощности, что ведёт к снижению КПД, поэтому фазы генератора соединяются только по схеме звезда.

Линейными называют напряжения между линейными проводами в порядке прямого чередования фаз.

Фазное напряжение –напряжение между началом и концом каждой фазы.

По характеру схемы при сопротивлениях линейных проводов, равных нулю, схема треугольник обеспечивает равенство линейных и фазных напряжений.

R_Aa=0 U_AB=U_ab

R_Bb=0 U_BC=U_bc

R_Cc=0 U_AC=U_ac

Введем соотношение между линейными и фазными токами.

Линейные токи – по проводам от генератора к нагрузке.

Фазные токи -по сопротивлениям нагрузки и совпадают с фазными напряжениями.

Построим векторную диаграмму напряжений и токов.

1. 
2. 

Рекомендуемый вариант первый – в виде равнолучевой звезды.

Для построения векторной диаграммы токов необходимо отложить углы сдвигов фаз φ между векторами фазного напряжения и фазного тока.

Построим векторную диаграмму линейных токов. Для этого запишем уравнения по первому закону Кирхгофа для точек a, b, c.

(.)a

(.)b

(.)c

Соединим AB и AC и направим в сторону AB.

Векторная диаграмма линейных токов представляет собой треугольник, очерченный относительно звезды фазных токов.

Введем понятие симметричной и несимметричной нагрузки.

Симметричная нагрузка –нагрузка, у которой комплексное сопротивление фаз одинаково.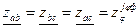

Несимметричная нагрузка –тинная нагрузка, у которой комплексные сопротивления не равны.

Для симметричной нагрузки, соединённой по схеме треугольник линейные токи построены на равнолучевой звезде фазных токов, образует равносторонний треугольник.

Итак, основные соотношения при соединении нагрузки звездой с нейтральным проводом I_Ф=Iл U_Л= 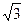U_Ф

А при соединении нагрузки треугольником U_Ф=Uл I_Л= 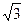I_Ф

Лекция №7

Анализ режимов работы трёхфазных нагрузок.

Вопросы:

1. Соединение по схеме звезда с нейтральным проводом (симметричная и несимметричная нагрузка).
2. Соединённых по схеме звезда без нейтрального провода (симметричная и несимметричная нагрузка).
3. Соединение по схеме треугольник
4. Аварийные режимы работ трёхфазных нагрузок

I. Соединение по схеме звезда с нейтральным проводом

Симметричная нагрузка.

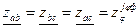
1. Показателем пригодности схемы для включения нагрузки является равенство фазных напряжений, которых эта схема обеспечивает.

Если сопротивления линейных и нейтрального проводов равно нулю, то в звезде с нейтральным проводом каждая фаза нагрузки соединена с генератором четырьмя проводами: линейными и нейтральным – генератор принудительно задаёт на нагрузку свои симметричные фазные напряжения.

1. Определяем фазные напряжения U_Л= 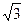U_Ф
2. Определим сопротивление, построив треугольник фазных сопротивлений.

z_Ф

X_Ф где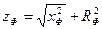

R_Ф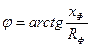

1. По закону Ома определим фазные токи
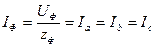
2. Определим линейные токи I_Л=I_Ф
3. Определим активную, реактивную и полную мощность всей трёхфазной нагрузки.

P_Ф=I²_ФR_Ф

Q_Ф=I²_Фx_ф

S_Ф=U_ФI_Ф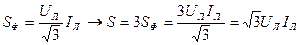

1. Определяем ток нейтрального провода. По первому закону Кирхгофа для точки n имеет фазный ток.

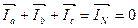
При симметричной нагрузке ток нейтрального провода равен нулю. А значит для включения симметричной нагрузки можно применить схему звезда без нейтрального провода.

Несимметричная нагрузка

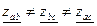
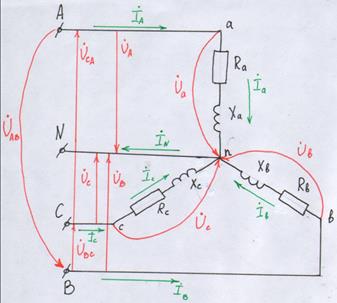
Обозначим на этой схеме линейные и фазные напряжения.

Кроме параметров схемы задано направление сети – линейное U_Л

1. Определим фазные напряжения. Если сопротивление фазы нагрузки подключено к генератору 4-мя проводами: линейными и нейтральным, то генератор принудительно задаёт на нагрузку свои симметричные фазные напряжения. U_A=U_B=U_C=U_Фе^jφ

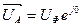
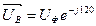
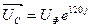
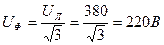
1. Для каждой фазы нагрузки строим треугольник сопротивлений и определяем полное сопротивление фазы и угол сдвига между напряжением и током.

Для А:

X_a Z_a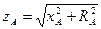

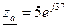
R_a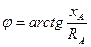

Для В: R_B=z_B z_B=R_B=10 φ_B=0, тогда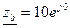

Для С: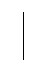

Z_C -X_C φ_c= -90, тогда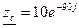

1. По закону Ома для каждой фазы находим фазные токи.

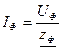
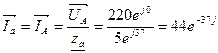
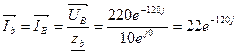
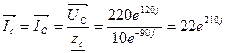
1. Определим линейные токи по формуле I_Ф=I_Л: I_a=I_A, I_b=I_B, I_c=I_C
2. Определим активную и реактивную мощность в каждой фазе. P_Ф=I_Ф²R_Ф
3. Определим активную и реактивную мощности всей трехфазной нагрузки:

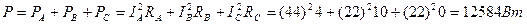
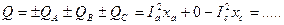
Где + - означает индуктивную нагрузку

- - означает ёмкостную нагрузку

7. Определяем ток нейтрального провода по первому закону Кирхгофа. 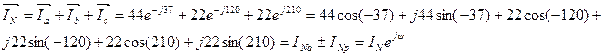8. Построим векторную диаграмму на комплексной плоскости и суммируем векторы.

Выводы:

1. Итак, соединение нагрузки звездой с нейтральным проводом всегда гарантирует равные фазные напряжения, не зависимо от сопротивлений фаз.

2. Для несимметричной нагрузки ток нейтрального провода не равен нулю а значит нейтральный провод необходим.

II. Соединение трёхфазной нагрузки звездой без нейтрального провода (симметричная нагрузка).

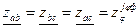
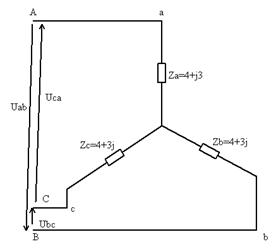
1. В данной схеме генератор задаёт на нагрузку только симметричную систему линейных напряжений U_AB и U_BC.

Так как нагрузка симметричная, то приложенные линейные напряжения распределяются поровну между прилегающими фазами. В результате Ua=U_b=U_c= 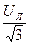а значит, что звезда без нейтрального провода пригодна для включения симметричной нагрузки.

Последовательность расчета смотрите для симметричной нагрузки, включённой по схеме «звезда с нейтральным проводом».

Соединение трёхфазной нагрузки звездой без нейтрального провода (несимметричная нагрузка).

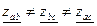
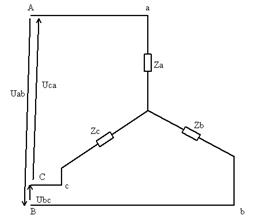
При несимметричной нагрузки, включённой по схеме «звезда без нейтрального провода», линейные напряжения генератора распределяются между прилегающими фазами, пропорционально их сопротивлениям, то есть на большем сопротивлении большее фазное напряжение, а на меньшем меньшее.

Требование обеспечения схемой равных фазных напряжений нарушается. Вывод: несимметричную нагрузку нельзя включать по схеме «звезда без нейтрального провода»