Задачи из лекций. (возможно, в билеты попадут не все они, но какая-то выборка из этих).

Задачи из лекций. (возможно, в билеты попадут не все они, но какая-то выборка из этих).

Лекция № 1

Пример. . Пример. .

Пример. . Пример. .

Пример. Пример. .

Пример. . Пример. .

Лекция № 2

Пример. . Пример. .

Пример. . Пример. .

Пример. . Пример. .

Лекция № 3 , , , , .

Пример. Вычислить .

Пример. Найти площадь фигуры, ограниченной линиями .

Пример. Вывести формулу объёма шара .

Лекция № 4

Вычислить , , .

Выяснить сходимость: , .

Вычислить , где есть квадрат: , .

Вычислить , D треугольник с вершинами (0,0), (1,0), (1,1).

Лекция № 5.

Пример. Сменить порядок интегрирования .

Пример. Вычислить интеграл где D куб .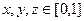

Пример. Вычислить интеграл где D - четверть круга единичного радиуса в первой четверти плоскости.

Пример. Доказать формулу площади круга с помощью полярных координат.

Пример. С помощью сферических координат вывести формулу объёма шара .

Лекция № 6.

Пример. Решить дифференциальное уравнение .

Пример. Решить уравнение .

Пример. Решить линейное уравнение .

Лекция № 7.

Пример. Решить уравнение 2 порядка .

Пример. Решить уравнение 3 порядка .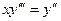

Пример.Решить уравнение .

Пример.Решить уравнение .

Пример. Решить уравнение .

Лекция № 8.

Пример. Решить уравнение методом Лагранжа (вариации произвольных постоянных).

Пример. Решить уравнение методом неопределённых коэффициентов (по виду правой части).

Пример. Решить систему с помощью сведения системы к одному уравнению.

Пример. Решить систему с помощью собственных чисел и векторов.

Лекция № 9.

Пример. Поделить в показательной форме.

Пример. Найти по формуле Муавра.

Пример. Найдите все значения корня .

Лекция № 10

Пример. Исследовать сходимость ряда .

Пример. Исследовать сходимость ряда .

Пример.Выяснить сходимость ряда .

Лекция № 11.

Пример.Выяснить сходимость .

Пример. Выяснить, сходится ли ряд .

Пример.Найти сумму ряда .

Пример. Найти сумму ряда .

Лекция № 12.

Пример. Разложить в ряд Тейлора с помощью геометрической прогрессии: по степеням 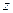, то есть в круге с центром 0.

Пример. Разложить в ряд Тейлора с помощью геометрической прогрессии: по степеням .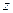

Пример. Разложить в ряд Тейлора с помощью геометрической прогрессии по степеням , то есть в круге с центром в точке 1.

Пример. Найти для .

Пример. решить с помощью степенных рядов.

Пример. Решить дифференциальное уравнение с помощью степенных рядов.

Пример. Найти кольцо сх ряда Лорана .

Лекция № 13

Пример. Разложить функцию :

а) в ряд Лорана в кольце

б) во внешней области

в) в ряд Тейлора в круге .

Пример. Разложить в ряд Лорана по степеням .

Пример. Найти скалярное произведение и на интервале (0,1).

Пример. Доказать, что функции , ортогональны на интервале .

Лекция № 14

Пример. Разложить в тригонометрический ряд Фурье функцию на интервале (-1,1).

Задачи из практики в билеты

(возможно, не все, но выборка из этих).

ПРАКТИКА № 1

Задача 11. Вычислить .

Ответ. .

ПРАКТИКА № 2

Задача 3. Вычислить . Ответ. .

Задача 4. Вычислить . Ответ. .

Задача 5. Вычислить . Ответ. .

Задача 7. Вычислить .

Ответ. .

Задача 8. Вычислить . Ответ. .

Задача 9. Вычислить . Ответ. .

Домашние задачи.

2. Ответ. . Указание. См. № 7.

3. . Ответ. . Указание. См. задачу № 9.

ПРАКТИКА № 3

Задача 2. Вычислить интеграл .

Ответ. .

Задача 3. Вычислить интеграл

Ответ. .

Задача 4.Вычислить интеграл .

Ответ. .

Задача 5. Вычислить интеграл .

Ответ. .

Задача 6. Вычислить интеграл

Ответ. = .

Задача 7. Вычислить .

Ответ. = .

Задача 8. Получить формулу вычисления интегралов вида .

Ответ.

ПРАКТИКА № 4

Задача 4. Вычислить интеграл .

Ответ. .

Задача 6. Вычислить интеграл .

Ответ.

Задача 7. Вычислить интеграл .

Ответ. .

Задача 8. Вычислить интеграл .

Ответ. .

Задача 9. Вычислить интеграл .

Ответ.

ПРАКТИКА № 5.

Задача 2. Вычислить интеграл .

Ответ. .

Задача 3. Вычислить интеграл .

Ответ. .

Задача 4.Вычислить интеграл .

Ответ. .

Ответ. .

Задача 6. Вычислить интеграл .

Ответ. .

Задача 8. Вычислить интеграл .

Ответ. .

Задача 9. Вычислить интеграл .

Ответ. .

Задача 10. Вычислить интеграл .

Ответ. .

ПРАКТИКА № 6.

Задача 1.Вычислить интеграл .

Ответ. .

Задача 2.Вычислить интеграл .

Ответ. .

Задача 5.Вычислить интеграл . Ответ. .

Задача 6.Вычислить интеграл . Ответ. .

ПРАКТИКА № 7

Задача 1. Вычислить интеграл . Ответ. .

Задача 2. Вычислить интеграл . Ответ. .

Задача 3. Вычислить интеграл . Ответ. .

Задача 4. Вычислить интеграл . Ответ. .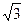

ПРАКТИКА № 8.

Задача 1. Найти площадь фигуры, ограниченной линиями:

и .

Ответ. .

Задача 2.Найти площадь области, ограниченной линиями

Ответ. .

Задача 4. Найти объём, получающийся при вращении кривой , при условии что .

Ответ. .

Задача 5. С помощью основной формулы объёмов тел вращения, доказать формулу объёма конуса .

Задача 6.Найти длину явно заданной кривой: .

Ответ. .

Задача 7.Найти длину 1 витка винтовой линии в пространстве

Ответ. .

Задача 8.Найти длину дуги х = cos³(2t), y =sin³(2t),

Ответ. 3.

Задача 9.Найти длину кривой, заданной в полярных координатах: , .

Ответ. .

ПРАКТИКА № 10.

Задача 2. Вычислить двойной интеграл 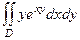, где D квадрат, .

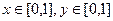Ответ. .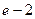

Задача 4. Вычислить интеграл 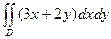по треугольнику D, вершины которого: (0,0),(1,1),(1,2).

Ответ. 2.

Задача 5.Сменить порядок интегрирования .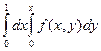

Ответ. .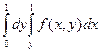

ПРАКТИКА № 11.

Задача 1. Изменить порядок интегрирования: .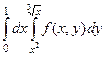

Ответ. .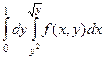

Задача 2. Сменить порядок интегрирования в двойном интеграле:

.

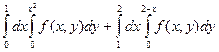Ответ. .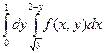

Задача 3. Изменить порядок интегрирования: .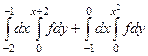

Ответ. .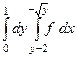

Задача 4.Вычислить 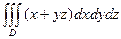по кубу .

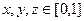Ответ. .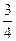

Задача 5. Вычислить тройной интеграл .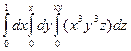

Ответ. .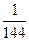

Задача 6. Найти объём тела, ограниченного поверхностями: .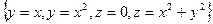

Ответ. .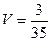

Задача 8. Вычислить 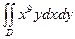, где D - четверть круга радиуса 1 (в первой координатной четверти).

Ответ. .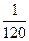

ПРАКТИКА № 12.

Задача 1. Записать в полярных координатах двойной интеграл по треугольнику с вершинами (0,0), (1,0), (1,1).

Ответ. .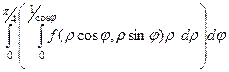

Задача 2. Найти площадь поверхности .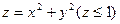

Ответ. .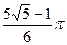

Задача 3. Вычислить объём тела, ограниченного цилиндром 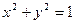и двумя плоскостями 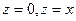в цилиндрических координатах.

Ответ. .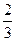

Задача 4.Вычислить определитель Якоби сферических координат.

Ответ. .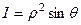

Задача 5. Плотность вещества в шаре радиуса 1 равна расстоянию от начала координат. Вычислить массу (в сферических координатах).

Ответ. .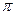

Задача 5-Б. Вычислить массу шара радиуса 1, если плотность равна квадрату расстояния от центра шара.

Ответ. .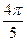

Задача 6.Найти объём тела, ограниченного конусом

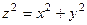и сферой радиуса .

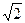Ответ. .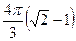

Задача 7.Найти объём тела, ограниченного поверхностями

.

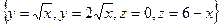Ответ. .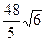

ПРАКТИКА № 13.

Задача 3.Решить дифференциальное уравнение .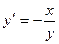

Ответ. .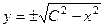

Задача 4. Решить уравнение 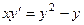, и найти частное решение задачи Коши: .

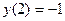Ответ. Общее решение 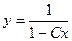, частное решение: .

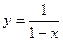ПРАКТИКА № 14.

Задача 1. Решить уравнение .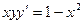

Ответ. .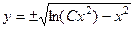

Задача 2. Решить уравнение .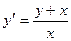

Ответ. .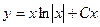

Уравнения Бернулли.

Задача 6. Решить дифференциальное уравнение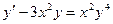

Ответ. .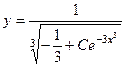

ПРАКТИКА № 15.

Задача 4. Найти общее решение дифф. уравнения .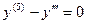

Ответ. .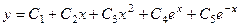

Задача 5.Найти частное решение дифференциального уравнения 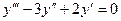при условиях Коши: .

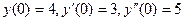Ответ. 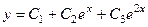, частное реш. .

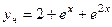Задача 6. Найти частное решение дифференциального уравнения 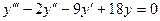при условиях Коши: .

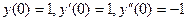Ответ. , .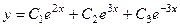

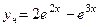Задача 9. Найти общее решение дифф. уравнения .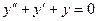

Ответ. .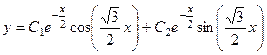

Задача 10. Уравнение 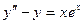решить методом Лагранжа

Ответ. .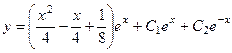

ПРАКТИКА № 16.

Задача 2. Решить уравнение: 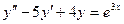методом неопределённых коэффициентов.

Ответ. .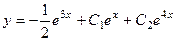

Задача 3.Решить уравнение .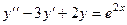

Ответ. .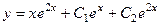

Задача 4.Решить уравнение .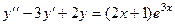

Ответ. .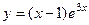

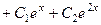Задача 5. Решить уравнение .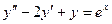

Ответ. .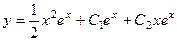

Задача 6. Решить уравнение 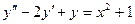методом неопределённых коэффициентов.

Ответ. .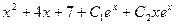

Задача домашняя. Решить уравнение. .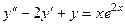

Ответ. .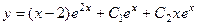

ПРАКТИКА № 17

Задача 6. Вычислить 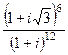Ответ. .

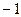Задача 7. Вычислить 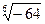. Ответ. 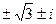и .

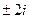Задача 9. Дано: 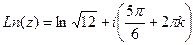. Найти .

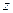Ответ. .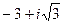

Задача 10. Найти все значения .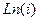

Ответ. .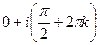

ПРАКТИКА № 19

Задача 1.Найти область сходимости ряда .

Ответ. абсолютно сходится в .

Задача 2. Найти область сходимости ряда .

Ответ. Ряд абсолютно сходится в интервале .

Задача 3. Найти область сходимости ряда .

Ответ. Ряд абсолютно сходится в интервале .

Задача 5. Найти радиус сходимости ряда . Ответ. .

Задача 6. Найти радиус сходимости ряда . Ответ. .

Задача 7. Найти радиус сходимости ряда . Ответ. .

Задача 9. Найти радиус сходимости ряда . Ответ. .

Задача 11. Найти сумму ряда Ответ. = .

Задача 12. Найти сумму ряда . Ответ. = .

Задача 13. Найти сумму ряда .

Ответ. = .

Задача 14. Найти сумму ряда .

Ответ. = .

ПРАКТИКА № 20

Задача 1. Найти сумму ряда . Ответ. = .

Задача 5. Найти для . Ответ.10.

Задача 6. Найти для . Ответ. = 21.

ПРАКТИКА № 21

Задача 1. Найти производную для . Ответ. .

Задача 3. Разложить в ряд Тейлора по степеням 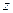и найти .

Ответ.Ряд , = .

Задача 4. Разложить в ряд Тейлора: по степеням .

Ответ. .

Задача 5. Разложить в ряд Тейлора: по степеням z.

Ответ.

Задача 6. Найти кольцо сходимости ряда Лорана:

Ответ. - кольцо сходимости.

Задача 9. Разложить в ряд Лорана во внешней области .

Ответ. .

ПРАКТИКА № 22. Ряды Фурье.

Задача 3. Найти ряд Фурье для

Ответ. Ряд Фурье: .

Ниже показан чертёж к этой задаче, получившийся в результате работы программы. Видно, что чем больше n, тем более точно кривая огибает ломаную.

Задача 4. Разложить в тригонометрический ряд Фурье: .

Ответ. Ряд Фурье: .

Задача 5. Разложить в тригонометрический ряд Фурье на интервале (-1,1).

Ответ. .

Задачи из лекций. (возможно, в билеты попадут не все они, но какая-то выборка из этих).

Лекция № 1

Пример. . Пример. .

Пример. . Пример. .

Пример. Пример. .

Пример. . Пример. .

Лекция № 2

Пример. . Пример. .

Пример. . Пример. .

Пример. . Пример. .

Лекция № 3 , , , , .

Пример. Вычислить .

Пример. Найти площадь фигуры, ограниченной линиями .

Пример. Вывести формулу объёма шара .

Лекция № 4

Вычислить , , .

Выяснить сходимость: , .

Вычислить , где есть квадрат: , .

Вычислить , D треугольник с вершинами (0,0), (1,0), (1,1).

Лекция № 5.

Пример. Сменить порядок интегрирования .

Пример. Вычислить интеграл где D куб .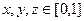

Пример. Вычислить интеграл где D - четверть круга единичного радиуса в первой четверти плоскости.

Пример. Доказать формулу площади круга с помощью полярных координат.

Пример. С помощью сферических координат вывести формулу объёма шара .

Лекция № 6.

Пример. Решить дифференциальное уравнение .

Пример. Решить уравнение .

Пример. Решить линейное уравнение .

Лекция № 7.

Пример. Решить уравнение 2 порядка .

Пример. Решить уравнение 3 порядка .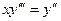

Пример.Решить уравнение .

Пример.Решить уравнение .

Пример. Решить уравнение .

Лекция № 8.

Пример. Решить уравнение методом Лагранжа (вариации произвольных постоянных).

Пример. Решить уравнение методом неопределённых коэффициентов (по виду правой части).

Пример. Решить систему с помощью сведения системы к одному уравнению.

Пример. Решить систему с помощью собственных чисел и векторов.

Лекция № 9.

Пример. Поделить в показательной форме.

Пример. Найти по формуле Муавра.

Пример. Найдите все значения корня .

Лекция № 10

Пример. Исследовать сходимость ряда .

Пример. Исследовать сходимость ряда .

Пример.Выяснить сходимость ряда .

Лекция № 11.

Пример.Выяснить сходимость .

Пример. Выяснить, сходится ли ряд .

Пример.Найти сумму ряда .

Пример. Найти сумму ряда .

Лекция № 12.

Пример. Разложить в ряд Тейлора с помощью геометрической прогрессии: по степеням 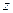, то есть в круге с центром 0.

Пример. Разложить в ряд Тейлора с помощью геометрической прогрессии: по степеням .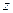

Пример. Разложить в ряд Тейлора с помощью геометрической прогрессии по степеням , то есть в круге с центром в точке 1.

Пример. Найти для .

Пример. решить с помощью степенных рядов.

Пример. Решить дифференциальное уравнение с помощью степенных рядов.

Пример. Найти кольцо сх ряда Лорана .

Лекция № 13

Пример. Разложить функцию :

а) в ряд Лорана в кольце

б) во внешней области

в) в ряд Тейлора в круге .

Пример. Разложить в ряд Лорана по степеням .

Пример. Найти скалярное произведение и на интервале (0,1).

Пример. Доказать, что функции , ортогональны на интервале .

Лекция № 14

Пример. Разложить в тригонометрический ряд Фурье функцию на интервале (-1,1).

Задачи из практики в билеты

(возможно, не все, но выборка из этих).

ПРАКТИКА № 1

Задача 11. Вычислить .

Ответ. .

ПРАКТИКА № 2

Задача 3. Вычислить . Ответ. .

Задача 4. Вычислить . Ответ. .

Задача 5.

Наши рекомендации