Условия равновесия стационарного процесса.

ЛЕКЦИЯ 1.

Химическая технология – область технологии, которая изучает процессы изменения составов внутренней структуры вещества в ходе химического превращения.

Наука о методах и средствах массовой химической переработки сырья, предметах потребления и средства производства.

Типовые стадии химической технологии:

1. Подготовка сырья;

2. Химико-технологический процесс (ХТП);

3. Выделение целевого продукта;

4. Очистка выбросов.

Все типовые стадии могут быть осуществлены за счет типовых процессов.

1 группа типовых процессов – механические (1);

В результате механических процессов изменяется форма и размеры материалов без изменения химических свойств (дробление, сортировка, классификация);

2 группа типовых процессов – гидромеханические (гидростатика и гидромеханика), (3,4);

Расчет основан на законах гидростатики и гидромеханики. Они включают в себя: перемещение жидкости по трубопроводам и аппаратам, гидро- и пневмотранспорт твердых материалов, разделение неоднородных смесей в системах жидкость/твердое, газ/твердое, жидкость/жидкость.

3 группа типовых процессов – тепловые (1,2,3,4);

Процессы переноса тепла от одной среды к другой нагревание и охлаждение, испарение и конденсация, выпаривание, перегонка.

4 группа типовых процессов – массообменные (2,3,4);

Перенос вещества из одной фазы в другую: абсорбция, десорбция, адсорбция, ректификация, дистилляция, сушка

5 группа типовых процессов– химические (2);

Изменение химических свойств и внутреннего строения вещества.

Теоретические основы ПАХТ.

1.Математическое описание процесса (основано на законах сохранения).

Включает:

· Расчет материального баланса процесса (ЗСМ),

· Составление теплового баланса (ЗСЭ),

· Баланс сил,

· Статика и кинетика процесса.

2.Физико-химические основы

· Основы термодинамики,

· Основы гидродинамики и гидростатики,

· Основы теплопередачи,

· Основы массопередачи.

3. Принципы моделирования:

· Физическое моделирование,

· Математическое моделирование,

· Математическое подобие процесса в маленьком процессе и большом.

4.Теория размерности.

Применение основных физических законов к изучению физических процессов.

I. Материальный баланс (основан на законе сохранения масс)

Хсм – концентрация твердого вещества в смеси [кг/кг],

Хосв - концентрация твердого вещества в осветленной жидкости,

Хос - концентрация твердого вещества в осадке.

Gсм,Gосв,Gос –материальные потоки [кг/с].

Gос

Gосв

Gсм

1.Общий вид материального баланса:

Gc=Gocв+Gос

2.Баланс по компоненту (по твердому веществу):

GcXc=GосвХосв+GосХос

3. Баланс по жидкости:

Gc(1-Xc)=Gосв(1-Хосв)+Gос(1-Хос)

4.

II. Тепловой баланс.

Кожухотрубчатый теплообменник.

1.Общий тепловой баланс:

Q₁+Q_п=Q₂+Q_k+Q_пот

Прежде чем составлять тепловой баланс процесса составляют материальный баланс.

Q₁=G₁C₁t_1; Q_п=DI_п;
Q₂=G₂C₂t_2; Q_k=D_ki_k, где D – количество пара,

I(i) - энтальпия
Все физические величины, сопутствующие расчету, могут быть взяты из справочной литературы.

ЛЕКЦИЯ 2.

ЛЕКЦИЯ 3.

Вязкость.

При движении реальных жидкостей или газов в них возникают силы внутреннего трения, которые оказывают сопротивление движению потока. Свойство жидкости или газа оказывать сопротивление усилиям, вызывающим относительное перемещение частиц, называется вязкость.

Материальный поток в виде жидкости или газа движется слоями:

За счет разности скоростей движения слоев возникает касательная сила, которую нужно приложить , чтобы относительно сдвинуть эти слои.

Величина Т пропорциональна поверхности контакта слоев F и отношению приращения величины скорости к расстоянию между слоями.

μ – коэффициент пропорциональности – динамический коэффициент вязкости (динамическая вязкость).

Сила сопротивления сдвигу – напряжение внутреннего трения.

Напряжение внутреннего трения, возникающие между слоями жидкости, пропорционально градиенту скорости.

В системе единиц СГС вязкость измеряется в пуазах (П) или сантипуазах (сП). Единица динамической вязкости в системе СИ в Па·с. Пересчетная формула: 1 Па·с = 10³ сП.

Динамическая вязкость – справочная величина.

Кинематическая вязкость n связана с динамической вязкостью соотношением:

В системе СГС единица кинематической вязкости 1 стокс (ст), в системе СИ 1 м²/с; пересчетная формула: 1 м²/с = 10⁴ ст.

Вязкость зависит от температуры, причем, для капельных жидкостей повышение температуры приводит к снижению вязкости, для газов при повышении температуры вязкость возрастает.

Те жидкости, которые подчиняются закону Ньютона, называются ньютоновскими.

Вязкость газов на практике – вязкость смеси.

,

где m1 ,m2 … mn -	вязкость компонентов смеси, Па·с;
mсм -	вязкость смеси газов, Па·с;
М1 ,М2…Мn , Мсм -	молекулярная масса компонентов смеси и самой смеси, кг/кмоль;
у1 , у2 …уn -	объемная или мольная доля компонентов;
Мсм -	молекулярная масса смеси газов, г/моль.

Молекулярная масса смеси газов рассчитывается по формуле:

Вязкость газа при любой температуре находится по уравнению Сутерленда.

,

где m0 -	вязкость при нормальных условиях (обычно берется из справочной литературы);
С -	константа Сутерленда
T -	абсолютная температура, К.

Гидростатика.

Давление.

Жидкость оказывает давление на дно и стенки сосуда, в котором она находится, а также на поверхность погруженного в нее тела.

Сила давления будет оказывать влияние по всем трем направлениям и направлена по нормали к площадке, на которую она действует. Давление в любой точке жидкости одинакого по всем направлениям (в противном случае происходило бы перемещение жидкости) и направлено по нормали к площадке, на которую оно действует.

В системе СИ давление измеряется в паскалях (Па).

1 Паскаль (Па) = 1 н/м². В системе МКГСС давление измеряется в кгс/м². Давление можно также выражать в метрах столба жидкости, что связано с методами измерения давления. Пересчетная формула:

,

где р -	давление в паскалях, Па;
r -	плотность жидкости, кг/м3;
g -	ускорение свободного падения, м/с2;
Н -	высота столба жидкости в метрах, м.

Разнообразные единицы давления и формулы для их пересчета приведены в литературе. Приведем наиболее важные расчетные соотношения:

1 атм (физическая) = 1,013 ·10⁵ Па = 10 м вод.ст.=1,033 кгс/см² = 760 мм рт.ст.

1 ат (техническая) = 9,81·10⁴ Па = 10 м вод.ст. = 1кгс/см² = 735 мм рт.ст.

1 мм вод.ст = 9,81 Па; 1 мм рт.ст = 133,3 Па.

1бар=10⁵Па.

Наиболее часто давление измеряют дифференциальными манометрами, которые представляют собой U-образную стеклянную трубку, заполненную рабочей жидкостью (вода, спирт, ртуть). Один конец трубки находится внутри аппарата или устройства, а второй открытый конец связан с атмосферой. Рассмотрим две возможные ситуации.

В первом случае, когда столб жидкости в левом колене трубки ниже, чем в правом, в аппарате создается избыточное давление и именно его измеряет манометр. Разность уровней жидкости в левом и правом коленах соответствует разности:

Dр = (р_атм + р_изб) – р_атм = р_изб

Аппарат   ратм – рразр

Аппарат   ратм + ризб

Рат

Рат

Dр = ризб

Dр = рразр

Во втором случае столбик жидкости в левом колене выше, чем в правом, р_атм выше, чем давление в аппарате. Тогда

Dр = р_атм - (р_атм - р_разр) = р_разр

Отсюда важный вывод: манометр никогда не показывает истинное (абсолютное) давление в аппарате, а показывает либо избыточное давление (то есть сверх атмосферного), либо разряжение (то есть недостающее до атмосферного давления).

Таким образом, для получения абсолютного давления в аппарате в первом случае к атмосферному добавляется избыточное давление, измеренное манометром, т.е.

р_абс = р_атм + р_изб ,

а во втором случае

р_абс = р_атм – р_разр.

Если в условиях задачи приводится избыточное давление, либо разряжение, значит для получения истинного абсолютного давления их необходимо пересчитать.

В гидростатике рассматривается равновесие жидкостей, находящихся в покое, при котором в жидкости отсутствует перемещение слоев относительно друг друга. В этом случае жидкости могут быть рассмотрены как идеальные.

Покой бывает: относительный и абсолютный.

Независимо от вида покоя на жидкость действуют сила давления и сила тяжести.

Зависимость между силами, действующими на жидкость, находящуюся в состоянии покоя, и определяющими условия равновесия жидкости, выражается дифференциальными уравнениями Эйлера.

Согласно основному принципу статики, сумма проекций на оси координат всех сил, действующих на элементарный объем жидкости, находящийся в равновесии, равно нулю. В противном случае происходило бы перемещение жидкости.

Ось z:

-gdm Аналогично записываем проекции сил по всем осям

Эти уравнения показывают, что давление в покоящейся жидкости изменяется только по вертикали, остальное одинаково в любой точке горизонтальной плоскости; изменение по оси X и Y равны нулю.

Для получения закона распределения давления во всем объеме покоящейся жидкости следует проинтегрировать данную систему уравнений, интегралом которой является основное уравнение гидростатики.

ЛЕКЦИЯ 4.

Давление на дно сосуда.

. (*)

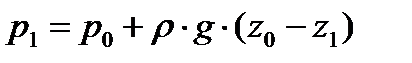Поскольку величина 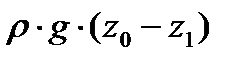постоянна, то при изменении величины р₀ на какую-либо величину, ровно настолько же изменится р₁ в любой другой точке жидкости. Выражение (*) может быть представлено как давление на дне сосуда, т.е.

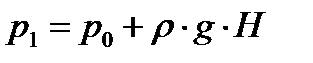, где: Н – высота жидкости в сосуде.

Из этого выражения видно, что давление на дне сосуда не зависит от его формы, а лишь от высоты столба жидкости над ним.

Закон Архимеда также вытекает из основного закона гидростатики и гласит: «на тело, погруженное в жидкость, действует направленная вверх сила, равная весу жидкости в погруженном объеме тела».

Техническое приложение основного закона гидростатики:

Сообщающиеся сосуды. Два сообщающихся сосуда заполнены жидкостями с различной плотностью r1 и r2 ( r1 > r2 ). Точка «а» лежит на границе раздела, которая находится в покое тогда, когда давление слева р1 равно давлению справа р2. Учитывая, что давление в обоих сосудах атмосферное, имеем:

paт

paт

r1

r2

а

h2

h1

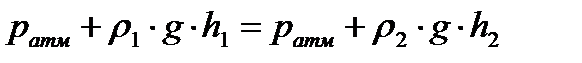, или:

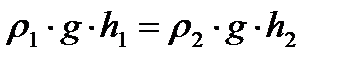, откуда: .

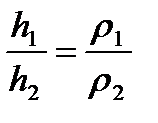Таким образом, в сообщающихся сосудах высота столба различных жидкостей обратно пропорциональна их плотности.

d1

d2

P

поршни

Гидравлический пресс. Давление, создаваемое левым поршнем, передается на правый поршень и, таким образом, на прессуемое тело. Здесь d₁ и d₂ – диаметры левого и правого поршня соответственно, р – гидроста-тическое давление.

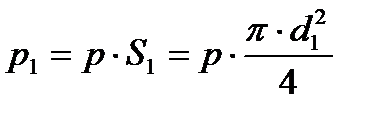
Сила давления на левый поршень,

а сила давления на правый поршень

.

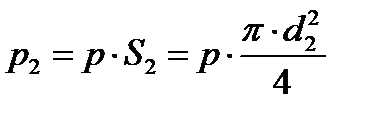Поскольку d₂ > d₁ , p₂ >p₁, то есть сила давления возрастает пропорционально площади сечения поршня. При этом не нужно забывать, что согласно золотому правилу механики мы выигрываем в силе (p₂ >p₁), но проигрываем в расстоянии, то есть правый поршень перемещается на меньшее расстояние, чем левый.

Дымовая труба является обязательным элементом тепловых установок: печей, котлов, сушилок и т.д. Воздух входит в тепловой агрегат за счет естественной тяги и выбрасывается как отработанный газ через дымовую трубу. Рассмотрим давление в точках «а» и «б».

Р0

Р0

печь

Газ

Воздух

h

;

,

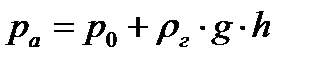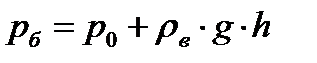где: р₀ – атмосферное давление;

а

б

r_г , r_в – плотность газа и воздуха, соответственно.

Движущая сила, обусловленная разностью плотностей воздуха и газа Dр = р_б – р_в = h ·g ·(r_в - r_г). Таким образом, в дымовой трубе имеет место не «тяга», а передавливание горячего газа в трубе столбом холодного воздуха.

Сифон используется для перемещения жидкости с верхнего уровня на нижний без использования насоса, т.е. самотеком.

Рассмотрим давление, действующее на точку «а» слева и справа. Обозначим через h₁ и h₂ расстояния от точки «а» до уровней жидкости в нижней и верхней емкостях.

h1

h2

P0

P0

а

.

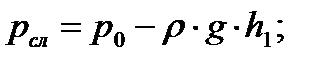
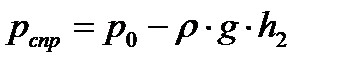Отметим, что знак минус обусловлен тем, что столбики жидкости в правом и левом колене стеклянной трубки находятся не над точкой «а», а под ней.

Движущая сила Dр = р_сл – р_спр = r ·g ·(h₂ – h₁).

Таким образом, благодаря разности столбов жидкости (h₂ – h₁) жидкость самопроизвольно перетекает из верхней емкости в нижнюю.

ГИДРОДИНАМИКА.

Изучает движение жидкости и газа.

Внутренняя задача гидродинамики связана с анализом движения жидкости и газа внутри труб и каналов.

Внешняя задача связана с изучением закономерностей обтекания жидкостью или газом различных тел.

Движущей силой при течении жидкости является разность давлений.

При перемещении жидкости разность давлений создается насосами.

Основные характеристики движения жидкости.

1. Скорость и расход.

· Количество жидкости, протекающей через поперечное сечение потока в единицу времени, называется расходом.

Различают объемный [м³/с] и массовый [кг/с] расход.

По сечению трубопровода скорость движения не одинакова.

· Средняя скорость движения потока жидкости – отношение объемного расхода жидкости к площади поперечного сечения.

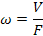
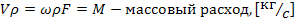
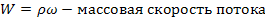
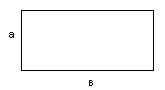
· Эквивалентный диаметр трубопровода.

При движении жидкости в трубах некруглого сечения используют величину эквивалентного диаметра (d_экв)

d_экв – диаметр гипотетического круглого сечения, у которого отношение площади поперечного сечения к смоченному периметру такое же как и трубопровода некруглого сечения.

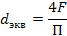
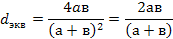
· Установившийся поток.

Движение жидкости в трубопроводе является установившемся или стационарным, если скорость частиц жидкости и другие параметры (плотность, температура, давление) не изменяются во времени для каждого сечения потока

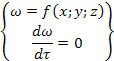
Нестационарный поток.

Все величины зависят не только от координат, но и от времени.

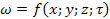
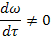
Установившиеся условия движения жидкости характерны для непрерывных процессов.

Неустановившееся движение – для периодических процессов, а также возникает кратковременно в периоды пуска и остановки непрерывных процессов.

· Режимы движения жидкости.

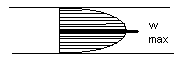
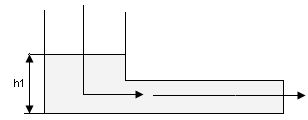Ламинарный режим наблюдается при малых скоростях или высокой вязкости жидкости. При этом жидкость движется параллельными слоями, не смешивающимися друг с другом.

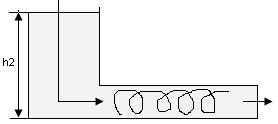
h₂>>h₁

Турбулентный режим – течение жидкости характеризуется вихревым движением потока, в котором присутствуют пульсации и завихрения. Создание турбулентного режима требует больших затрат энергии по сравнению с ламинарным.

Опыты Рейнольдса показали, что переход от ламинарного движения к турбулентному тем легче, чем выше массовая скорость жидкости и длина трубы и чем меньше динамическая вязкость жидкости.

Критерий Рейнольдса:

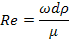
Величина критерия Рейнольдса определяет режим движения жидкости.

Ламинарный режим ω_ср=0,5ω_max

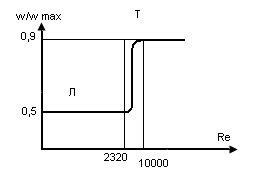
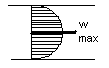Турбулентный режим ω_ср=(0,7÷0,9)ω_max

ЛЕКЦИЯ 5

Режим движения жидкости по трубопроводам оказывает первостепенное влияние на процессы тепло- и массопереноса. Необходима высокая турбулизация потока. Независимо от развитости турбулентного режима у стенки трубы турбулентное движение всегда сопровождается ламинарным. И это определяет сопротивления движению жидкости за счет наличия сил трения.

Уравнение неразрывности потока.

Устанавливает общую зависимость между скоростями в потоке жидкости, для которого соблюдается условие сглаженности (неразрывности) движения.

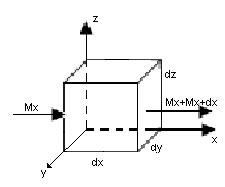
Рассмотрим движение жидкости по трем направлениям.

ОХ: Mx=ρω_xdydzdτ

Mx – количество вещества, зашедшее от х за единицу времени.

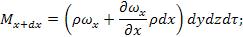
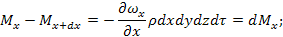
OY:

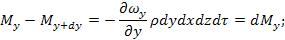
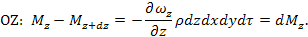
Общее накопление массы вещества в единице объема составит:

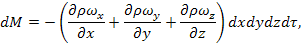
В соответствии с законом сохранения массы сумма накоплений в единице объема dV должна быть равна убыли массы в этом объеме за время dτ, т.е.

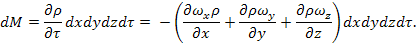
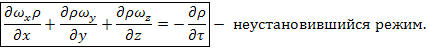
Полученное выражение представляет собой дифференциальное уравнение неразрывности потока для неустановившегося режима движения.

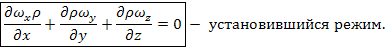
Уравнение неразрывности выражает закон сохранения массы для неустановившегося и установившегося режима движения.

Представим систему: труба, по которой движется материальный поток (установившийся режим).

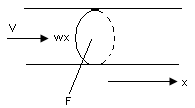
В случае одномерного движения вдоль оси X: 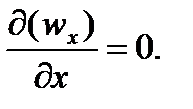После умножения на сечение трубопровода F имеем: 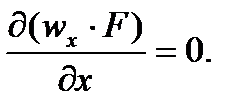Тогда:

w ·F =V = const.

Полученное выражение является уравнением расхода, показывающим, что при движении несжимаемой жидкости объемный расход жидкости (V) остается постоянным в любом сечении трубопровода.

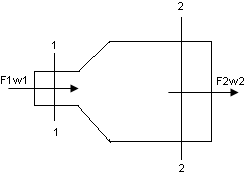Тогда для двух произвольных сечений трубопровода 1 и 2 имеем: w₁F₁=w₂F₂ , а 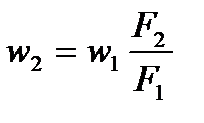, то есть скорость жидкости в трубопроводе изменяется обратно пропорционально сечению. Когда площадь сечения возрастает, скорость падает, и наоборот.

Полученные уравнения позволяют при заданном режиме движения жидкости рассчитать площадь поперечного сечения

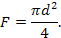
Дифференциальные уравнения Эйлера.

Рассмотрим установившийся поток идеальной жидкости, движущийся через элементарный объем dV=dxdydz

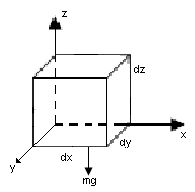Рассмотрим проекции всех действующих сил на соответствующие оси (смотреть уравнение Эйлера для покоящейся жидкости).

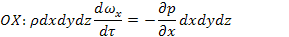
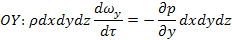
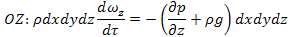
Согласно основному принципу динамики, сумма проекций сил, действующих на движущийся элементарный объем жидкости по трем направлениям, равна произведению массы жидкости на ее ускорение по соответствующим осям.

В итоге:

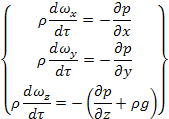
Полученная система уравнений представляет собой дифференциальные уравнения идеальной жидкости для установившегося режима.

ДУ Навье-Стокса.

Описывают движение реальной вязкой жидкости, в которой помимо сил давления и тяжести действуют и силы трения.

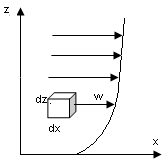
При наличии сил трения имеет место касательная сила и касательное напряжение τ (движение внутреннего трения).

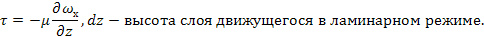
При учете наличия всех сил ДУ Навье-Стокса выглядит следующим образом:

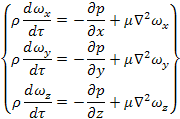
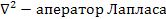
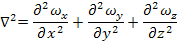
Уравнение Бернулли.

Решение уравнений Эйлера называется уравнением Бернулли.

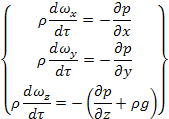
Разделим правую и левую части на ρ и соответственно умножим на dx, dy, dz.

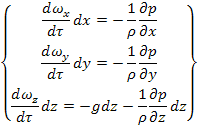
Складываем правую и левую части с учетом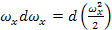

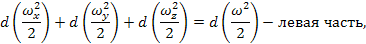
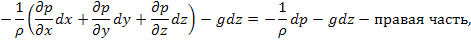
Разделим обе части на g

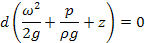
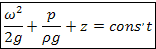
z – геометрический напор;

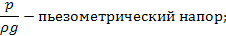
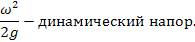
Согласно уравнению Бернулли, сумма статистического и динамического напоров при установившемся движении идеальной жидкости является постоянной, т.е., если по каким-либо причинам изменяется один из напоров, то на ту же величину в сумме изменятся и остальные.

ЛЕКЦИЯ 6.

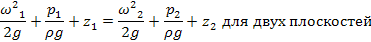
Уравнение Бернулли является частным случаем закона сохранения энергии и выражает энергетический баланс материального потока для идеальных жидкостей.

Для реальных жидкостей, при их движении по трубопроводу, начинают действовать силы внутреннего трения, обусловленные

· Вязкостью жидкости;

· Режимом движения;

· Силами трения о стенки трубы.

Эти силы оказывают сопротивление движению жидкости – гидравлическое сопротивление. На его преодоление должна расходоваться некоторая часть энергии потока. Поэтому общее количество энергии потока, т.е. сумма потенциальной и кинетической, по длине трубопровода будет снижаться.

(Епот+Ек)₁=(Епот+Ек)₂+Еп

Еп – потерянная энергия.

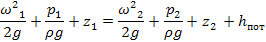
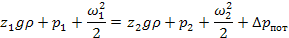
hпот представляет собой удельную энергию, расходуемую на преодоление гидравлического сопротивления при движении реальной жидкости.

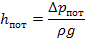
Практические приложения уравнения Бернулли.

1. Определение расхода

V=ωF

ω₁F₁=ω₂F₂

Чтобы найти объемный расход жидкости, необходимо знать скорость и площадь поперечного сечения.

Принципы измерения скорости и расхода жидкости:

· Пневматические трубки (трубка Пито);

· Дроссельные приборы, включающие в себя диафрагму и трубу Вентури.

В трубке Пито-Прандляиспользуется другой принцип измерения. В центре трубопровода помещают две трубки, а и б, соединенные с дифманометром. Размещение трубок в трубопроводе таково, что трубка «а» измеряет статический напор р_ст , а трубка «б» - суммарно статический и скоростной напоры р_ст + р_ск , то есть полный напор.

w

rм

Трубка Пито-Прандля

а

б

Dр

Следовательно, разность уровней в манометре соответствует величине скоростного напора.

.

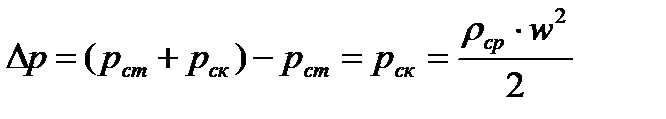Отсюда можно выразить максимальную скорость по оси трубопровода:

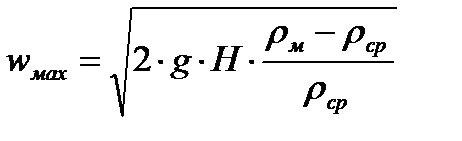м/с.

Зная отношение средней по сечению скорости к максимальной по оси находим среднюю скорость: 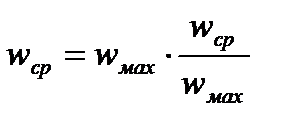, м/с, а затем объемный расход: 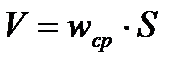, м³/с.

Dp

d1; w1

rср d2; w2

rм

Измерительная диафрагма

Измерительная диафрагмапредставляет собой перегородку в трубопроводе с центральным круглым отверстием. Протекая через отверстие диафрагмы, среда увеличивает свою скорость с w₁ до w₂ . При этом часть статического напора затрачивается на увеличение кинетической энергии по уравнению Бернулли.

Величину Dр можно замерить дифференциальным манометром. Этот манометр измеряет перепад давления Н, который является напором для истечения газа (жидкости) через отверстие диафрагмы. Запишем уравнение Бернулли:

.

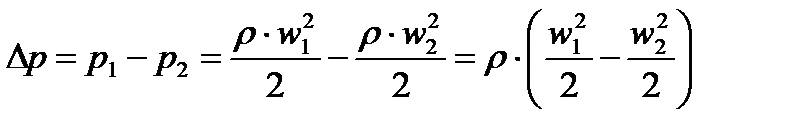Скорость истечения через отверстие:

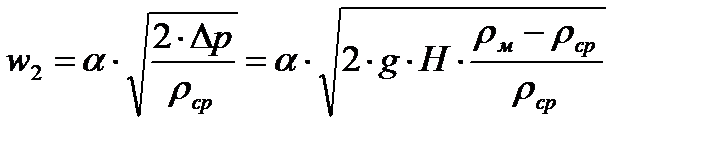, м/с ,

где r_м и r_ср - плотность жидкости в манометре и плотность среды соответственно, кг/м³;

a - коэффициент расхода.

Н - разность уровней жидкости в дифманометре, м.

Объемный расход воздуха:

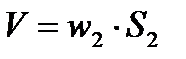, м/с, где 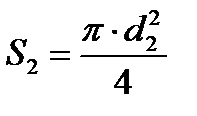- сечение отверстия в диафрагме, м².

Скорость среды в трубопроводе:

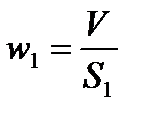, м/с, где 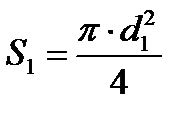- сечение трубопровода, м².

Истечение жидкостей и газов через отверстия также, как и работа насосов, подчиняется уравнению Бернулли. Из открытого бака происходит истечение жидкости через отверстие в днище диаметром d₀. Высота уровня жидкости в баке Н; этот уровень поддерживается постоянным. Скорость перемещения жидкости в баке и в отверстии соответственно w₁ и w₀ . Запишем уравнение Бернулли в точке «а» и в точке «в» (Р₀ – атмосферное давление):

плоскость сравнения

р0

w0

w1

z1

z2

H

р0

d0

Восполнение

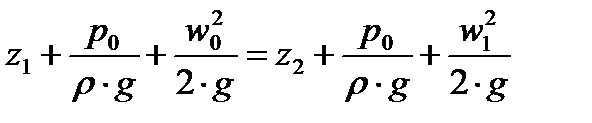;отсюда:

а

.

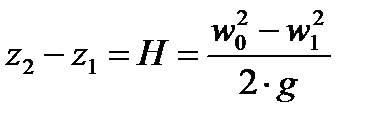в

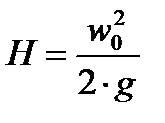Поскольку скорость перемещения жидкости в баке можно принять равной нулю (уровень жидкости постоянный), то Откуда скорость истечения из отверстия:

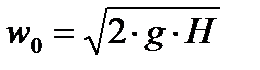,м/с .

Н – высота жидкости в баке, а в более общем случае – напор истечения. Если бак закрытый и давление в нем р отличается от атмосферного, то в выражении вместо величины Н подставляют величину :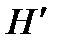

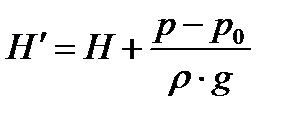, м .

Если в баке избыточное давление, то величина р – р₀ = р_изб , то есть 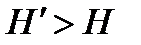. Это означает, что скорость истечения возрастает. Если в баке разряжение, то величина (р – р₀) – отрицательная т.к. р < р₀ , то есть 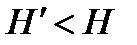. Это означает, что скорость истечения снизится по сравнению с открытым баком, либо жидкость вообще не потечет ( ).

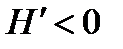Скорость истечения с учетом местных сопротивлений при выходе жидкости из отверстия

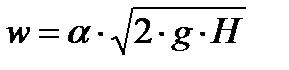, м/с.

ЛЕКЦИЯ 7.

ЛЕКЦИЯ 8.

Подобными называются явления, для которых постоянны отношения характеризующих их сходственных величин.

Необходимые условия подобия:

· Геометрическое подобие, т.е. подобие сходственных геометрических величин.

· Временное подобие.

· Подобие полей физических величин, т.е. в сходных точках пространства физические величины подобны.

· Подобие начальных и граничных условий.

Достаточные условия:

Процессы, происходящие в модели и в натуре, должны описываться одинаковыми дифференциальными уравнениями.

Основные понятия теории подобия.

К_l изменяется при изменении масштаба.

i – представляет собой выражение величины в относительных единицах.

Инвариант, выраженный отношением двух подобных величин, называется симплексом.

Если инвариант выражен отношениями разнородных величин, но является безразмерным, то такой инвариант называется критерием подобия.

· Геометрическое подобие соблюдается при равенстве всех сходных линейных размеров

1 аппарат	2 аппарат
Загрузка	τ1'	τ1''
Перемешивание	τ2'	τ2''
Нагрев	τ3'	τ3''
Выгрузка	τ4'	τ4''

· Временное подобие

При соблюдении геометрического и временного подобия будет соблюдаться и подобие скоростей

т.е. можно заменить отношение одноименных величин отношениями их приращений.

· Подобие полей физических величин.

Оно предполагает, что для двух любых сходных точек натуры и модели, размещенных подобно в пространстве и времени, отношение физических свойств является величиной постоянной.

· Подобие начальных и граничных условий предполагает, что отношение основных параметров в начале и на границе в модели и в натуре является величиной постоянной, т.е. для начальных и граничных условий, а также для других сходных точек пространства, соблюдается геометрическое, временное и физическое подобие.

Теоремы подобия.

1. Подобными являются явления, характеризующиеся численно равными критериями подобия.

m'	m''
ω'	ω''
τ'	τ''
G'	G''

Эти величины взаимодействуют по закону:

Запишем константы подобия:

Если индикатор подобия равен 1, то явления подобны.

Вывод:эта теорема подобия была сформулирована Ньютоном и согласно ей, при подобии систем всегда могут быть найдены такие комплексные величины, которые для сходств точек одинаковы. Первая точка подобия, показывает, какие величины следует измерять при проведении опытов, а именно те величины, которые входят в критерии подобия.

2. Решение любого дифференциального уравнения связывающего между собой. Переменные, влияющие на процесс, могут быть предоставлены в виде зависимости между критериями подобия.

П₁, П₂, П₃…….. П₁=f(П₂;П₃…)

Если процесс описывает несколько критериев подобия П₁, П₂, П_3, … такая зависимость называется критериальным уравнением; причем, П₁ – определяемый критерий, П₂, П_3, - определяющий критерий. П₁ – это такой критерий, в который входят величины, не являющиеся необходимыми для однозначной характеристики процесса. Такие критерии сами зависят от определяющих критериев, в состав которых входят условия однозначности, то есть замеряемые величины.

Для гидродинамических процессов нужно найти ∆р – эта величина будет входить в П₁. Замеряемые величины (вязкость, плотность, диаметр и т.д.) – П₂,П₃

Вывод: Вторая теорема подобия показывает, как обрабатывать результаты опытов, проводимых на моделях. Их нужно представлять