Квантовая статистика. Фазовое пространство. Функция распределения

Рис. 312

Если (Е- Е_F)>> kT («хвост» функции распределения), то единицей в знаменателе (236.2) можно пренебречь по сравнению с экспонентой и тогда распределение Ферми — Дирака переходит в распределение Максвелла — Больцмана. Таким образом, при (Е Е_F)<<kT, т. е. при больших значениях энергии, к электронам в металле применима классическая статистика, в то же время, когда (Е Е_F)<<kT, к ним применима только квантовая статистика Ферми — Дирака.

Выводы квантовой теории электропроводности металлов

Квантовая теория электропроводности металлов — теория электропроводности, основывающаяся на квантовой механике и квантовой статистике Ферми — Дирака, — пересмотрела вопрос об электропроводности металлов, рассмотренный в классической физике. Расчет электропроводности металлов, выполненный на основе этой теории, приводит к выражению для удельной электрической проводимости металла

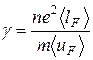(238.1)

которое по внешнему виду напоминает классическую формулу (103.2) для γ, но имеет совершенно другое физическое содержание. Здесь n — концентрация электронов проводимости в металле, < l_F > — средняя длина свободного пробега электрона, имеющего энергию Ферми,

<u_F > — средняя скорость теплового движения такого электрона.

Выводы, получаемые на основе формулы (238.1), полностью соответствуют опытным данным. Квантовая теория электропроводности металлов, в частности, объясняет зависимость удельной проводимости от температуры: γ~1/Т (классическая теория (см. § 103) дает, что γ~1/√Т), а также аномально большие величины (порядка сотен периодов решетки) средней длины свободного пробега электронов в металле (см. § 103).

Квантовая теория рассматривает движение электронов с учетомих взаимодействия с кристаллической решеткой. Согласно корпускулярно-волновому дуализму, движению электрона сопоставляют волновой процесс. Идеальная кристаллическая решетка (в ее узлах находятся неподвижные частицы и в ней отсутствуют нарушения периодичности) ведет себя подобно оптически однородной среде — она «электронные волны» не рассеивает. Это соответствует тому, что металл не оказывает электрическому току — упорядоченному движению электронов — никакого сопротивления. «Электронные вол вы», распространяясь в идеальной кристаллической решетке, как бы огибают узлы решетки и проходят значительные расстояния. В реальной кристаллической решетке всегда имеются неоднородности, которыми могут быть, например, примеси, вакансии; неоднородности обусловливаются также тепловыми колебаниями. В реальной кристаллической решетке происходит рассеяние «электронных волн» на неоднородностях, что и является причиной электрического сопротивления металлов. Рассеяние «электронных волн» на неоднородностях, связанных с тепловыми колебаниями, можно рассматриватькак столкновения электронов с фононами.

Согласно классической теории, <u>~√T, поэтому она не смогла объяснить истинную зависимость γ от температуры (см. § 103). В квантовой теории средняя скорость <u_F> от температуры практически не зависит, так как доказывается, что с изменением температуры уровень Ферми остается практически неизменным. Однако с повышением температуры рассеяние «электронных волн» на тепловых колебаниях решетки (на фононах) возрастает, что соответствует уменьшению средней длины свободного пробега электронов. В области комнатных температур (1_F)~Т^-1, поэтому, учитывая независимость <u> от температуры, получим, что сопротивление металлов (R~1/γ) в соответствии с данными опытов растет пропорционально Т. Таким образом, квантовая теория электропроводности металлов устранила и эту трудность классической теории.

Квантовая статистика. Фазовое пространство. Функция распределения

Квантовая статистика — раздел статистической физики, исследующий системы, которые состоят из огромного числа частиц, подчиняющихся законам квантовой механики.

В отличие от входных положений классической статистической физики, в которой тождественные частицы различимы (частицу можно отличить от всех таких же частиц), квантовая статистика основывается на принципе неразличимости тождественных частиц (см. § 226). При этом оказывается, как будет показано ниже, что коллективы частиц с целым и полуцелым спинами подчиняются разным статистикам.

Пусть система состоит из N частиц. Введем в рассмотрение многомерное пространство всех координат и импульсов частиц системы. Тогда состояние системы определяется заданием 6N переменных, так как состояние каждой частицы определяется тройкой координат x,у, z, t тройкой соответствующих проекций импульса рх, рy, рz.Соответственно число «взаимно перпендикулярных» координатных осей данного пространства равно 6N. Это бN-мерное пространство называется фазовым пространством. Каждому микросостоянию системы отвечает точка в бN-мерном фазовом пространстве, так как задание точки фазового пространства означает задание координат и импульсов всех частиц системы. Разобьем фазовое пространство на малые бN - мерные элементарные ячейки объемом dgdp = dg₁dg₂,…dg_N, где g — совокупность координат всех частиц, р — совокупность проекций их импульсов. Корпускуляр-но-волновой дуализм свойств вещества (см. § 213) и соотношение неопределенностей Гейзенберга (см. § 215) приводят к выводу, что объем элементарной ячейки (он называется фазовым объемом) не может быть меньше чем h³ (А — постоянная Планка).

Вероятность dW данного состояния системы можно представить с помощью функции распределения ƒ(g, р):

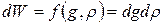(234.1)

Здесь dW—вероятность того, что точка фазового пространства попадет в элемент фазового объема ада/», расположенного вблизи данной точки g,р. Иными словами, а dW представляет собой вероятность того, что система находится в состоянии, в котором ее координаты и импульсы заключены в интервале g, g+dg р, р+dр.

Согласно формуле (234.1), функция распределения есть не что иное, как плотность вероятности определенного состояния системы. Поэтому она должна быть нормирована на единицу:

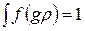
где интегрирование производится по всему фазовому пространству.

Зная функцию распределения ƒ(g, р), можно решить основную задачу квантовой статистики — определить средние значения величин, характеризующих рассматриваемую систему. Среднее значение любой функции

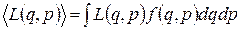(234.2)

Если иметь дело не с координатами и импульсами, а с энергией, которая квантуется, то состояние системы характеризуется не непрерывной, а дискретной функцией распределения.

Явное выражение функции распределения в самом общем виде получил американский физик Д.Гиббс (1839—1903). Оно называется каноническим распределением Гиббса. В квантовой статистике каноническое распределение Гиббса имеет вид

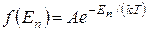(234.3)

где A — постоянная, определяемая из условия нормировки к единице, n — совокупность всех квантовых чисел, характеризующих данное состояние. Подчеркнем, чтоƒ(E_n)есть именновероятность данного состояния, а не вероятность того, что система имеет определенное значение энергииЕ_n так как данной энергии может соответствовать не одно, а несколько различных состояний (может иметь место вырождение).