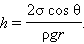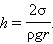Кинематика. Равномерное прямолинейное движения: определение, уравнение перемещения, координаты. Графики зависимости Х (t).
Часть 1
Равноускоренное движение: определение, уравнение перемещения, координаты. Графики зависимости V (t).
Равноускоренное прямолинейное движение — это такое движение, при котором скорость тела за равные промежутки времени изменяется одинаково, другими словами, это движение с постоянным ускорением.
Траектория движения в данном случае— прямая линия.
a=const — уравнение ускорения. Т. е а имеет численное значение, которое не изменяется со временем.
По определению ускорения 
Отсюда мы уже нашли уравнения для зависимости скорости от времени: v = v0 + at.
Посмотрим, как это уравнение можно использовать для графического представления равноускоренного движения.
Изобразим графически зависимости кинематических величин от времени для трех тел
. 
1 тело движется вдоль оси 0Х, при этом увеличивает свою скорость (вектор ускорения а сонаправленн с вектором скорости v). vx >0, ах > 0
2 тело движется вдоль оси 0Х, при этом уменьшает свою скорость (вектор ускорения а не сонаправленн с вектором скорости v). vx >0, ах < 0
2 тело движется против оси 0Х, при этом уменьшает свою скорость (вектор ускорения а не сонаправленн с вектором скорости v). vx < 0, ах > 0
 График ускорения
График ускорения
Ускорение по определению величина постоянная. Тогда для представленной ситуации график зависимости ускорения от времени a(t) будет иметь вид:
Из графика ускорения можно определить как изменялась скорость – увеличивалась или уменьшалась и на какое численное значение изменилась скорость и у какого тела скорость больше изменилась.
График скорости
Если сравнить зависимость координаты от времени при равномерном движении и зависимость проекции скорости от времени при равноускоренном движении, можно увидеть, что эти зависимости одинаковы:
х= х0 + vx t vx = v0x + aхt
Это значит, что и графики зависимостей имеют одинаковый вид.Для построения этого графика на оси абсцисс откладывают время движения, а на оси ординат - скорость (проекцию скорости) тела. В равноускоренном движении скорость тела с течением времени изменяется.
При равноускоренном прямолинейном движении скорость тела определяется формулой
vx = v0x + aхt
В этой формуле υ0 – скорость тела при t = 0 (начальная скорость), a = const – ускорение. На графике скорости υ (t) эта зависимость имеет вид прямой линии (рис. ).
По наклону графика скорости может быть определено ускорение a тела. Соответствующие построения выполнены на рис. для графика I. Ускорение численно равно отношению сторон треугольника ABC:

Масса. Плотность.
Масса— одна из самых фундаментальных физических величин. Масса характеризует сразу несколько свойств тела и обладает рядом важных свойств.
1) Масса служит мерой содержащегося в теле вещества.
2) Масса является мерой инертности тела. Инертностью называется свойство тела сохра- нять свою скорость неизменной (в инерциальной системе отсчёта), когда внешние воз- действия отсутствуют или компенсируют друг друга. При наличии внешних воздействий инертность тела проявляется в том, что его скорость меняется не мгновенно, а постепенно, и тем медленнее, чем больше инертность (т. е. масса) тела.
3) Массы тел являются причиной их гравитационного притяжения друг к другу (см. листок «Закон всемирного тяготения»).
4) Масса тела равна сумме масс его частей. Это так называемая аддитивность массы. Ад- дитивность позволяет использовать для измерения массы эталон — 1 кг.
5) Масса изолированной системы тел не меняется со временем (закон сохранения массы).
6) Масса тела не зависит от скорости его движения. Масса не меняется при переходе от одной системы отсчёта к другой. Перечисленные свойства имеют место в классической механике Ньютона. В теории относи- тельности некоторые из этих утверждений перестают быть справедливыми. Мы обсудим это в соответствующем листке.
Плотностью однородного тела называется отношение массы тела к его объёму: ρ = m/ V .
Плотность не зависит от геометрических свойств тела (формы, объёма) и является характе- ристикой вещества тела. Плотности веществ представлены в справочных таблицах. Желательно помнить плотность воды: 1000 кг/м3.
4)Силы в природе. Виды сил, примеры проявления, формула расчета, коэффициенты пропорциональности.
Сила- векторная величина. Необходимо знать точку приложения и направление каждой силы. Важно уметь определить какие именно силы действуют на тело и в каком направлении. Сила обозначается как  , измеряется в Ньютонах. Для того, чтобы различать силы, их обозначают следующим образом
, измеряется в Ньютонах. Для того, чтобы различать силы, их обозначают следующим образом 
Ниже представлены основные силы, действующие в природе. Придумывать не существующие силы при решении задач нельзя!
Сил в природе много. Здесь рассмотрены силы, которые рассматриваются в школьном курсе физики при изучении динамики. А также упомянуты другие силы, которые будут рассмотрены в других разделах.
Сила тяжести
На каждое тело, находящееся на планете, действует гравитация Земли. Сила, с которой Земля притягивает каждое тело, определяется по формуле


Точка приложения находится в центре тяжести тела. Сила тяжести всегда направлена вертикально вниз.

Сила трения
Познакомимся с силой трения. Эта сила возникает при движении тел и соприкосновении двух поверхностей. Возникает сила в результате того, что поверхности, если рассмотреть под микроскопом, не являются гладкими, как кажутся. Определяется сила трения по формуле:


Сила приложена в точке соприкосновения двух поверхностей. Направлена в сторону противоположную движению.

Так как тело представляем в виде материальной точки, силу можно изображать с центра
Сила реакции опоры
Представим очень тяжелый предмет, лежащий на столе. Стол прогибается под тяжестью предмета. Но согласно третьему закону Ньютона стол воздействует на предмет с точно такой же силой, что и предмет на стол. Сила направлена противоположно силе, с которой предмет давит на стол. То есть вверх. Эта сила называется реакцией опоры. Название силы "говорит" реагирует опора. Эта сила возникает всегда, когда есть воздействие на опору. Природа ее возникновения на молекулярном уровне. Предмет как бы деформировал привычное положение и связи молекул (внутри стола), они, в свою очередь, стремятся вернуться в свое первоначальное состояние, "сопротивляются".
Абсолютно любое тело, даже очень легкое (например,карандаш, лежащий на столе), на микроуровне деформирует опору. Поэтому возникает реакция опоры.
Специальной формулы для нахождения этой силы нет. Обозначают ее буквой  , но эта сила просто отдельный вид силы упругости, поэтому она может быть обозначена и как
, но эта сила просто отдельный вид силы упругости, поэтому она может быть обозначена и как 
Сила приложена в точке соприкосновения предмета с опорой. Направлена перпендикулярно опоре.

Так как тело представляем в виде материальной точки, силу можно изображать с центра
Сила упругости
Это сила возникает в результате деформации (изменения первоначального состояния вещества). Например, когда растягиваем пружину, мы увеличиваем расстояние между молекулами материала пружины. Когда сжимаем пружину - уменьшаем. Когда перекручиваем или сдвигаем. Во всех этих примерах возникает сила, которая препятствует деформации - сила упругости.
Закон Гука


 Сила упругости направлена противоположно деформации.
Сила упругости направлена противоположно деформации.
Так как тело представляем в виде материальной точки, силу можно изображать с центра
При последовательном соединении, например, пружин жесткость рассчитывается по формуле
 При параллельном соединении жесткость
При параллельном соединении жесткость

Вес тела
 Вес тела - это сила, с которой предмет воздействует на опору. Вы скажете, так это же сила тяжести! Путаница происходит в следующем: действительно часто вес тела равен силе тяжести, но это силы совершенно разные. Сила тяжести - сила, которая возникает в результате взаимодействия с Землей. Вес - результат взаимодействия с опорой. Сила тяжести приложена в центре тяжести предмета, вес же - сила, которая приложена на опору (не на предмет)!
Вес тела - это сила, с которой предмет воздействует на опору. Вы скажете, так это же сила тяжести! Путаница происходит в следующем: действительно часто вес тела равен силе тяжести, но это силы совершенно разные. Сила тяжести - сила, которая возникает в результате взаимодействия с Землей. Вес - результат взаимодействия с опорой. Сила тяжести приложена в центре тяжести предмета, вес же - сила, которая приложена на опору (не на предмет)!
Формулы определения веса нет. Обозначается эта силы буквой  .
.
Сила реакции опоры или сила упругости возникает в ответ на воздействие предмета на подвес или опору, поэтому вес тела всегда численно одинаков силе упругости, но имеет противоположное направление.
 Сила реакции опоры и вес - силы одной природы, согласно 3 закону Ньютона они равны и противоположно направлены. Вес - это сила, которая действует на опору, а не на тело. Сила тяжести действует на тело.
Сила реакции опоры и вес - силы одной природы, согласно 3 закону Ньютона они равны и противоположно направлены. Вес - это сила, которая действует на опору, а не на тело. Сила тяжести действует на тело.
Вес тела может быть не равен силе тяжести. Может быть как больше, так и меньше, а может быть и такое, что вес равен нулю. Это состояние называется невесомостью. Невесомость - состояние, когда предмет не взаимодействует с опорой, например, состояние полета: сила тяжести есть, а вес равен нулю!

Определить направление ускорения возможно, если определить, куда направлена равнодействующая сила
Обратите внимание, вес - сила, измеряется в Ньютонах. Как верно ответить на вопрос: "Сколько ты весишь"? Мы отвечаем 50 кг, называя не вес, а свою массу! В этом примере, наш вес равен силе тяжести, то есть примерно 500Н!
Перегрузка - отношение веса к силе тяжести
Сила Архимеда
Сила возникает в результате взаимодействия тела с жидкость (газом), при его погружении в жидкость (или газ). Эта сила выталкивает тело из воды (газа). Поэтому направлена вертикально вверх (выталкивает). Определяется по формуле:


В воздухе силой Архимеда пренебрегаем.
Если сила Архимеда равна силе тяжести, тело плавает. Если сила Архимеда больше, то оно поднимается на поверхность жидкости, если меньше - тонет.

Электрические силы
Существуют силы электрического происхождения. Возникают при наличии электрического заряда. Эти силы, такие как сила Кулона, сила Ампера, сила Лоренца, подробно рассмотрены в разделе Электричество.
Размеры
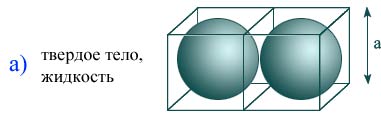
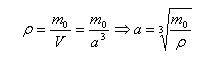 Оценка размера молекулы может быть сделана как размер кубика a в котором содержится одна молекула, исходя из плотности твердых или жидких веществ и массы одной молекулы:
Оценка размера молекулы может быть сделана как размер кубика a в котором содержится одна молекула, исходя из плотности твердых или жидких веществ и массы одной молекулы:
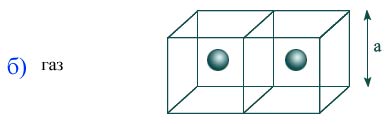
Масса молекулОтношение массы вещества m к числу молекул N в данном веществе: 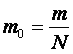
Относительная молекулярная массаОтношение массы молекулы (или атома) данного вещества к 1/12 массы атома углерода:
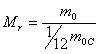
Количество вещества
Количество вещества равно отношению числа частиц N в теле (атомов – в атомарном веществе, молекул – в молекулярном) к числу молекул в одном моле веществаNА:
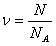
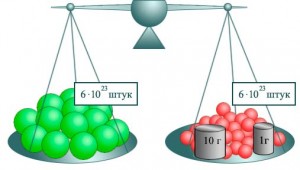 Постоянная Авогадро
Постоянная Авогадро
Количество молекул, содержащихся в 1 моль вещества.
Молярная масса
Молярной массой вещества называют массу вещества, взятого в количестве 1 моля.
В Международной системе единиц молярная масса вещества выражается в кг/моль.
Взаимодействие (количественно на основе опытов)
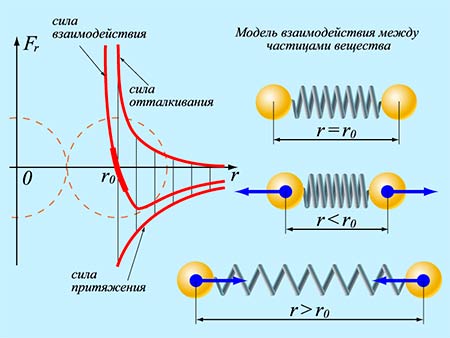 Для взаимодействия молекул характерно одновременно и притяжение, и отталкивание: на расстояниях r<r0доминирует отталкивание, на расстоянииr>r0 – притяжение, причем оно быстро убывает. На расстоянииr0 система двух молекул обладает минимумом потенциальной энергии (сила взаимодействия равна нулю) – это состояние устойчивого равновесия
Для взаимодействия молекул характерно одновременно и притяжение, и отталкивание: на расстояниях r<r0доминирует отталкивание, на расстоянииr>r0 – притяжение, причем оно быстро убывает. На расстоянииr0 система двух молекул обладает минимумом потенциальной энергии (сила взаимодействия равна нулю) – это состояние устойчивого равновесия
Молекулярно-кинетическая теория дает возможность понять, почему вещество может находиться в газообразном, жидком и твердом состояниях. С точки зрения МКТ агрегатные состояния различаются по значению среднего расстояния между молекулами и характеру движения молекул друг относительно друга.
Основные положения молекулярно-кинетической теории неоднократно подтверждались различными физическими экспериментами. Например, исследованием:
Диффу́зия — процесс взаимного проникновения молекул или атомов одного вещества между молекулами или атомами другого, приводящий к самопроизвольному выравниванию их концентраций по всему занимаемому объёму. В некоторых ситуациях одно из веществ уже имеет выравненную концентрацию и говорят о диффузии одного вещества в другом. При этом перенос вещества происходит из области с высокой концентрацией в область с низкой концентрацией (вдоль вектора градиента концентрации).
Шкала температур Кельвина
Основная статья:Кельвин
Понятие абсолютной температуры было введено У. Томсоном (Кельвином), в связи с чем шкалу абсолютной температуры называют шкалой Кельвина или термодинамической температурной шкалой. Единица абсолютной температуры — кельвин (К).
Абсолютная шкала температуры называется так, потому что мера основного состояния нижнего предела температуры — абсолютный ноль, то есть наиболее низкая возможная температура, при которой в принципе невозможно извлечь из вещества тепловую энергию.
Абсолютный ноль определён как 0 K, что равно −273,15 °C и -459,67 °F.
Шкала температур Кельвина — это шкала, в которой начало отсчёта ведётся от абсолютного нуля.
Важное значение имеет разработка на основе термодинамической шкалы Кельвина Международных практических шкал, основанных на реперных точках — фазовых переходах чистых веществ, определенных методами первичной термометрии. Первой международной температурной шкалой являлась принятая в 1927 г. МТШ-27. С 1927 г. шкала несколько раз переопределялась (МТШ-48, МПТШ-68, МТШ-90): менялись реперные температуры, методы интерполяции, но принцип остался тот же — основой шкалы является набор фазовых переходов чистых веществ с определенными значениями термодинамических температур и интерполяционные приборы, градуированные в этих точках. В настоящее время действует шкала МТШ-90. Основной документ (Положение о шкале) устанавливает определение Кельвина, значения температур фазовых переходов (реперных точек)[43] и методы интерполяции.
Используемые в быту температурные шкалы — как Цельсия, так и Фаренгейта (используемая, в основном, в США), — не являются абсолютными и поэтому неудобны при проведении экспериментов в условиях, когда температура опускается ниже точки замерзания воды, из-за чего температуру приходится выражать отрицательным числом. Для таких случаев были введены абсолютные шкалы температур.Одна из них называется шкалой Ранкина, а другая — абсолютной термодинамической шкалой (шкалой Кельвина); температуры по ним измеряются, соответственно, в градусах Ранкина (°Ra) и кельвинах (К). Обе шкалы начинаются при температуре абсолютного нуля. Различаются они тем, что цена одного деления по шкале Кельвина равна цене деления шкалы Цельсия, а цена деления шкалы Ранкина эквивалентна цене деления термометров со шкалой Фаренгейта. Температуре замерзания воды при стандартном атмосферном давлении соответствуют 273,15 K, 0 °C, 32 °F.
Масштаб шкалы Кельвина привязан к тройной точке воды (273,16 К), при этом от неё зависит постоянная Больцмана. Это создаёт проблемы с точностью интерпретации измерений высоких температур. Сейчас Международное бюро мер и весов рассматривает возможность перехода к новому определению кельвина, основанному на фиксации численного значения постоянной Больцмана, вместо привязки к температуре тройной точки[44].
Шкала Цельсия
Основная статья: Градус Цельсия
В технике, медицине, метеорологии и в быту в качестве единицы измерения температуры используется шкала Цельсия. В настоящее время в системе СИ термодинамическую шкалу Цельсия определяют через шкалу Кельвина: t(°С) = Т(К) — 273,15 (точно), т. е. цена одного деления в шкале Цельсия равна цене деления шкалы Кельвина. По шкале Цельсия температура тройной точки воды равна приблизительно 0,008 °C,[45] и, следовательно, точка замерзания воды при давлении в 1 атм очень близка к 0 °C. Точка кипения воды, изначально выбранная Цельсием в качестве второй реперной точки со значением, по определению равным 100 °C, утратила свой статус одного из реперов. По современным оценкам температура кипения воды при нормальном атмосферном давлении в термодинамической шкале Цельсия составляет около 99,975 °C. Шкала Цельсия очень удобна с практической точки зрения, поскольку вода очень распространена на нашей планете и на ней основана наша жизнь. Ноль Цельсия — особая точка для метеорологии, поскольку связана с замерзанием атмосферной воды. Шкала предложена Андерсом Цельсием в 1742 г.
Шкала Фаренгейта
Основная статья: Градус Фаренгейта
В Англии и, в особенности, в США используется шкала Фаренгейта. Ноль градусов Цельсия — это 32 градуса Фаренгейта, а 100 градусов Цельсия — 212 градусов Фаренгейта.
В настоящее время принято следующее определение шкалы Фаренгейта: это температурная шкала, 1 градус которой (1 °F) равен 1/180 разности температур кипения воды и таяния льда при атмосферном давлении, а точка таяния льда имеет температуру +32 °F. Температура по шкале Фаренгейта связана с температурой по шкале Цельсия (t °С) соотношением t °С = 5/9 (t °F — 32), t °F = 9/5 t °С + 32. Предложена Г. Фаренгейтом в 1724 году.
Шкала Реомюра
Основная статья:Градус Реомюра
Предложена в 1730 году Р. А. Реомюром, который описал изобретённый им спиртовой термометр.
Единица — градус Реомюра (°Ré), 1 °Ré равен 1/80 части температурного интервала между опорными точками — температурой таяния льда (0 °Ré) и кипения воды (80 °Ré) 1 °Ré = 1,25 °C.
В настоящее время шкала вышла из употребления, дольше всего она сохранялась во Франции, на родине автора.
Виды деформации
· растяжение-сжатие,
· сдвиг,
· изгиб,
· кручение.
В большинстве практических случаев наблюдаемая деформация представляет собой совмещениенескольких одновременных простых деформаций. В конечном счёте, однако, любую деформацию можносвести к двум наиболее простым: растяжению (или сжатию) и сдвигу.
Механическое напряжение.
Состояние упруго деформированного тела характеризуют величиной σ, называемой механическим напряжением.
Механическое напряжение σ равно отношению модуля силы упругости Fупр к площади поперечного сечения тела S:
σ=FynpS σ=FynpS .
Измеряется механическое напряжение в Па: [σ] = Н/м2 = Па.
Наблюдения показывают, что при небольших деформациях механическое напряжение σ пропорционально относительному удлинению ε:
σ=E⋅|ε| σ=E⋅|ε| . (2)
Эта формула является одним из видов записи закона Гука для одностороннего растяжения (сжатия). В этой формуле относительное удлинение взято по модулю, так как оно может быть и положительным и отрицательным.
Коэффициент пропорциональности Е в законе Гука называется модулем упругости (модулем Юнга). Экспериментально установлено, что
модуль Юнга численно равен такому механическому напряжению, которое должно было бы возникнуть в теле при увеличении его длины в 2 раза.
Докажем это: Из закона Гука получаем, что E=σε E=σε . Если модуль Юнга E численно равен механическому напряжению σ, то ε=Δll0=1 ε=Δll0=1 . Тогда Δl=l−l0=l0;l=2l0 Δl=l−l0=l0;l=2l0 .
Измеряется модуль Юнга в Па: [E] = Па/1 = Па.
Практически любое тело (кроме резины) при упругой деформации не может удвоить свою длину: значительно раньше оно разорвется. Чем больше модуль упругости Е, тем меньше деформируется стержень при прочих равных условиях (l0, S, F). Таким образом, модуль Юнга характеризует сопротивляемость материала упругой деформации растяжения или сжатия.
Закон Гука, записанный в форме (2), легко привести к виду (1). Действительно, подставив в (2) σ=FynpS σ=FynpS и ε=Δll0 ε=Δll0 , получим:
FynpS=E⋅Δll0 FynpS=E⋅Δll0 или Fynp=E⋅Sl0⋅Δl Fynp=E⋅Sl0⋅Δl ,
где E⋅Sl0=k E⋅Sl0=k .
Термодинамика
Раздел молекулярной физики, который изучает передачу энергии, закономерности превращения одних видов энергии в другие. В отличие от молекулярно-кинетической теории, в термодинамике не учитывается внутреннее строение веществ и микропараметры.
Термодинамическая система
Это совокупность тел, которые обмениваются энергией (в форме работы или теплоты) друг с другом или с окружающей средой. Например, вода в чайнике остывает, происходит обмен теплотой воды с чайником и чайника с окружающей средой. Цилиндр с газом под поршнем: поршень выполняет работу, в результате чего, газ получает энергию, и изменяются его макропараметры.
Количество теплоты
Это энергия, которую получает или отдает система в процессе теплообмена. Обозначается символом Q, измеряется, как любая энергия, в Джоулях.
В результате различных процессов теплообмена энергия, которая передается, определяется по-своему.
Нагревание и охлаждение
Этот процесс характеризуется изменением температуры системы. Количество теплоты определяется по формуле
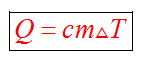
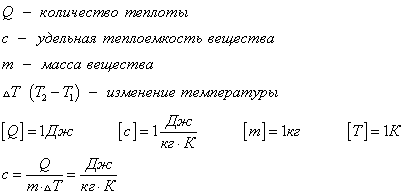
Удельная теплоемкость вещества с измеряется количеством теплоты, которое необходимо для нагревания единицы массы данного вещества на 1К. Для нагревания 1кг стекла или 1кг воды требуется различное количество энергии. Удельная теплоемкость - известная, уже вычисленная для всех веществ величина, значение смотреть в физических таблицах.
Теплоемкость вещества С - это количество теплоты, которое необходимо для нагревания тела без учета его массы на 1К.
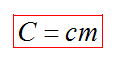
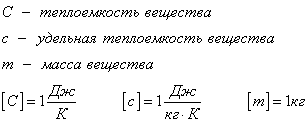
Плавление и кристаллизация
Плавление - переход вещества из твердого состояния в жидкое. Обратный переход называется кристаллизацией.
Энергия, которая тратится на разрушение кристаллической решетки вещества, определяется по формуле
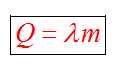
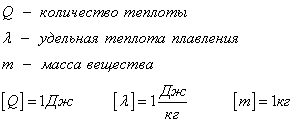
Удельная теплота плавления известная для каждого вещества величина, значение смотреть в физических таблицах.
Парообразование (испарение или кипение) и конденсация
Парообразование - это переход вещества из жидкого (твердого) состояния в газообразное. Обратный процесс называется конденсацией.
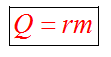
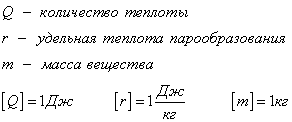
Удельная теплота парообразования известная для каждого вещества величина, значение смотреть в физических таблицах.
Горение
Количество теплоты, которое выделяется при сгорании вещества
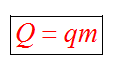
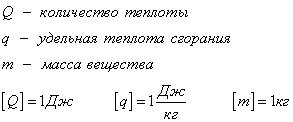
Удельная теплота сгорания известная для каждого вещества величина, значение смотреть в физических таблицах.
Для замкнутой и адиабатически изолированной системы тел выполняется уравнение теплового баланса. Алгебраическая сумма количеств теплоты, отданных и полученных всеми телами, участвующим в теплообмене, равна нулю:
Q1+Q2+...+Qn=0
23) Строение жидкостей. Поверхностный слой. Сила поверхностного натяжения: примеры проявления, расчет, коэффициент поверхностного натяжения.
Время от времени любая молекула может переместиться в соседнее вакантное место. Такие перескоки в жидкостях происходят довольно часто; поэтому молекулы не привязаны к определенным центрам, как в кристаллах, и могут перемещаться по всему объему жидкости. Этим объясняется текучесть жидкостей. Из-за сильного взаимодействия между близко расположенными молекулами они могут образовывать локальные (неустойчивые) упорядоченные группы, содержащие несколько молекул. Это явление называется ближним порядком (рис. 3.5.1).
Вследствие плотной упаковки молекул сжимаемость жидкостей, т. е. изменение объема при изменении давления, очень мала; она в десятки и сотни тысяч раз меньше, чем в газах. Например, для изменения объема воды на 1 % нужно увеличить давление приблизительно в 200 раз. Такое увеличение давления по сравнению с атмосферным достигается на глубине около 2 км.
Жидкости, как и твердые тела, изменяют свой объем при изменении температуры. Для не очень больших интервалов температур относительное изменение объема ΔV / V0пропорционально изменению температуры ΔT:
|
Коэффициент β называют температурным коэффициентом объемного расширения. Этот коэффициент у жидкостей в десятки раз больше, чем у твердых тел. У воды, например, при температуре 20 °С βв ≈ 2·10–4 К–1, у стали βст ≈ 3,6·10–5 К–1, у кварцевого стекла βкв ≈ 9·10–6 К–1.
Тепловое расширение воды имеет интересную и важную для жизни на Земле аномалию. При температуре ниже 4 °С вода расширяется при понижении температуры (β < 0). Максимум плотности ρв = 103 кг/м3 вода имеет при температуре 4 °С.
При замерзании вода расширяется, поэтому лед остается плавать на поверхности замерзающего водоема. Температура замерзающей воды подо льдом равна 0 °С. В более плотных слоях воды у дна водоема температура оказывается порядка 4 °С. Благодаря этому жизнь может существовать в воде замерзающих водоемов.
Наиболее интересной особенностью жидкостей является наличие свободной поверхности. Жидкость, в отличие от газов, не заполняет весь объем сосуда, в который она налита. Между жидкостью и газом (или паром) образуется граница раздела, которая находится в особых условиях по сравнению с остальной массой жидкости.. Следует иметь ввиду, что вследствие крайне низкой сжимаемости наличие более плотно упакованного поверхностного слоя не приводит к сколь-нибудь заметному изменению объема жидкости. Если молекула переместится с поверхности внутрь жидкости, силы межмолекулярного взаимодействия совершат положительную работу. Наоборот, чтобы вытащить некоторое количество молекул из глубины жидкости на поверхность (т. е. увеличить площадь поверхности жидкости), внешние силы должны совершить положительную работу ΔAвнеш, пропорциональную изменению ΔS площади поверхности:
| ΔAвнеш = σΔS. |
Коэффициент σ называется коэффициентом поверхностного натяжения (σ > 0). Таким образом, коэффициент поверхностного натяжения равен работе, необходимой для увеличения площади поверхности жидкости при постоянной температуре на единицу.
В СИ коэффициент поверхностного натяжения измеряется в джоулях на метр квадратный (Дж/м2) или в ньютонах на метр (1 Н/м = 1 Дж/м2).Следовательно, молекулы поверхностного слоя жидкости обладают избыточной по сравнению с молекулами внутри жидкости потенциальной энергией. Потенциальная энергия Eр поверхности жидкости пропорциональна ее площади:
|
Из механики известно, что равновесным состояниям системы соответствует минимальное значение ее потенциальной энергии. Отсюда следует, что свободная поверхность жидкости стремится сократить свою площадь. По этой причине свободная капля жидкости принимает шарообразную форму. Жидкость ведет себя так, как будто по касательной к ее поверхности действуют силы, сокращающие (стягивающие) эту поверхность. Эти силы называются силами поверхностного натяжения.
Наличие сил поверхностного натяжения делает поверхность жидкости похожей на упругую растянутую пленку, с той только разницей, что упругие силы в пленке зависят от площади ее поверхности (т. е. от того, как пленка деформирована), а силы поверхностного натяжения не зависят от площади поверхности жидкости.
Некоторые жидкости, как, например, мыльная вода, обладают способностью образовывать тонкие пленки. Всем хорошо известные мыльные пузыри имеют правильную сферическую форму – в этом тоже проявляется действие сил поверхностного натяжения. Если в мыльный раствор опустить проволочную рамку, одна из сторон которой подвижна, то вся она затянется пленкой жидкости (рис. 3.5.3).
Силы поверхностного натяжения стремятся сократить поверхность пленки. Для равновесия подвижной стороны рамки к ней нужно приложить внешнюю силу 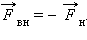 Если под действием силы
Если под действием силы 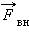 перекладина переместится на Δx, то будет произведена работа ΔAвн = FвнΔx = ΔEp = σΔS, где ΔS = 2LΔx – приращение площади поверхности обеих сторон мыльной пленки. Так как модули сил
перекладина переместится на Δx, то будет произведена работа ΔAвн = FвнΔx = ΔEp = σΔS, где ΔS = 2LΔx – приращение площади поверхности обеих сторон мыльной пленки. Так как модули сил 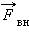 и
и 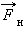 одинаковы, можно записать:
одинаковы, можно записать:
|
Таким образом, коэффициент поверхностного натяжения σ может быть определен как модуль силы поверхностного натяжения, действующей на единицу длины линии, ограничивающей поверхность.
Из-за действия сил поверхностного натяжения в каплях жидкости и внутри мыльных пузырей возникает избыточное давление Δp. Если мысленно разрезать сферическую каплю радиуса R на две половинки, то каждая из них должна находиться в равновесии под действием сил поверхностного натяжения, приложенных к границе разреза длиной 2πR и сил избыточного давления, действующих на площадь πR2 сечения (рис. 3.5.4). Условие равновесия записывается в виде
| σ2πR = ΔpπR2. |
Отсюда избыточное давление внутри капли равно
|
Избыточное давление внутри мыльного пузыря в два раза больше, так как пленка имеет две поверхности:
|
Если эти силы больше сил взаимодействия между молекулами самой жидкости, то жидкость смачивает поверхность твердого тела. В этом случае жидкость подходит к поверхности твердого тела под некоторым острым углом θ, характерным для данной пары жидкость – твердое тело. Угол θ называется краевым углом. Если силы взаимодействия между молекулами жидкости превосходят силы их взаимодействия с молекулами твердого тела, то краевой угол θ оказывается тупым (рис. 3.5.5). В этом случае говорят, что жидкость не смачивает поверхность твердого тела. При полном смачиванииθ = 0, при полном несмачиванииθ = 180°.
Капиллярными явлениями называют подъем или опускание жидкости в трубках малого диаметра – капиллярах. Смачивающие жидкости поднимаются по капиллярам, несмачивающие – опускаются.
На рис. 3.5.6 изображена капиллярная трубка некоторого радиуса r, опущенная нижним концом в смачивающую жидкость плотности ρ. Верхний конец капилляра открыт. Подъем жидкости в капилляре продолжается до тех пор, пока сила тяжести 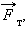 действующая на столб жидкости в капилляре, не станет равной по модулю результирующей Fнсил поверхностного натяжения, действующих вдоль границы соприкосновения жидкости с поверхностью капилляра: Fт = Fн, где Fт = mg = ρhπr2g, Fн = σ2πr cos θ.
действующая на столб жидкости в капилляре, не станет равной по модулю результирующей Fнсил поверхностного натяжения, действующих вдоль границы соприкосновения жидкости с поверхностью капилляра: Fт = Fн, где Fт = mg = ρhπr2g, Fн = σ2πr cos θ.
Отсюда следует:
|
При полном смачивании θ = 0, cos θ = 1. В этом случае
|
При полном несмачивании θ = 180°, cos θ = –1 и, следовательно, h < 0. Уровень несмачивающей жидкости в капилляре опускается ниже уровня жидкости в сосуде, в которую опущен капилляр.
Вода практически полностью смачивает чистую поверхность стекла. Наоборот, ртуть полностью не смачивает стеклянную поверхность. Поэтому уровень ртути в стеклянном капилляре опускается ниже уровня в сосуде.
24) Парообразование: определение, виды (испарение, кипение), расчет количества теплоты на парообразование и конденсацию, удельная теплота парообразования.
Испарение и конденсация. Объяснение явления испарения на основе представлений о молекулярном строении вещества. Удельная теплота парообразования. Ее единицы.
Явление превращения жидкости в пар называется парообразованием.
Испарение-процесс парообразования, происходящий с открытой поверхности.
Молекулы жидкости движутся с разными скоростями. Если какая-нибудь молекула окажется у поверхности жидкости, она может преодолеть притяжение соседних молекул и вылететь из жидкости. Вылетевшие молекулы образуют пар. У оставшихся молекул жидкости при соударении меняются скорости. Некоторые молекулы при этом приобретают скорость, достаточную для того, чтобы вылететь из жидкости. Этот процесс продолжается, поэтому жидкости испаряются медленно.
*Скорость испарения зависит от рода жидкости. Быстрее испаряются те жидкости, у которых молекул притягиваются с меньшей силой..
*Испарение может происходить при любой температуре. Но при высоких температурах испарение происходит быстрее.
*Скорость испарения зависит от площади ее поверхности.
*При ветре (потоке воздуха) испарение происходит быстрее.
При испарении внутренняя энергия уменьшается, т.к. при испарении жидкость покидают быстрые молекулы, следовательно, средняя скор

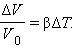
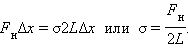
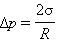 (капля жидкости).
(капля жидкости). 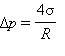 (мыльный пузырь).
(мыльный пузырь).