Теплопроводность через плоскую стенку. Термические сопротивления

1. Однородная стенка. Рассмотрим однородную стенку толщиной (рис. 1-7), коэффициент теплопроводности , которой постоянен. На наружных поверхностях стенки поддерживаются постоянные температуры . Температура изменяется только в направлении оси х. В этом случае температурное поле одномерно, изотермические поверхности плоские и располагаются перпендикулярно оси х.

На расстоянии х выделим внутри стенки слой толщиной ограниченный двумя изотермическими поверхностями. На основании закона Фурье [уравнение (1-1)] для этого случая можно написать:

Термическое сопротивление — тепловое сопротивление, способность тела (его поверхности или какого-либо слоя) препятствовать распространению теплового движения молекул.

Теплопроводность через цилиндрическую стенку. Линейное термическое сопротивление

Передача теплоты через цилиндрическую стенку имеет большое практиче­ское значение, так как многие теплотехнические агрегаты (теплообменные аппараты, гильзы цилиндров двигателей внутреннего сгорания и другие) имеют элементы в виде цилиндрических труб. Передача теплоты теплопро­водностью в цилиндрической стенке происходит по тем же законам, что и в плоской стенке. Различие заключается лишь в том, что плоская стенка имеет поверхности одинаковые по площади, а у цилиндрической площадь внутренней поверхности всегда меньше наружной.

Рассмотрим цилиндр длиной L (рис. 14.4). Внутренняя и внешняя пло­щади поверхностей цилиндра Si и 52 имеют температуры соответственно Ti иТ2, причем Ti > Т2. Тепловой поток направлен по нормали к поверх­ности цилиндра (по радиусам ее сечений) изнутри наружу. Внутренний и наружный диаметры равны соответственно D\ и d2. Теплопроводность материала стенки постоянна и равна А.

У , Рис. 14.4. К расчету теплопроводности цилиндрической стенки

Q

Ш

Для того чтобы воспользоваться законом Фурье, выделим внутри стен­ки кольцевой слой радиусом г и толщиной dr. Тепловой поток, проходящий

Через этот слой, равен

Ф = A(-gradT)L = — А ^ 2тгг£, [Вт], (14.11)

Аг

Где L — высота (длина) цилиндра.

Разделив переменные в выражении (14.11), получаем

27ГА L Г

Интегрируя это уравнение в пределах изменения радиуса от Г\ до г2 и температуры от Ti до Т2 получим:

Та г2

Ti п

Отсюда определяем тепловой поток, прошедший через стенку,

Ф = |^(Г1_Т2) = ^:(Г1_Г2)) [Вт]. (14.12)

RL Dl Так как площади внутренней и внешней поверхностей различны, то различными оказываются и соответствующие плотности потока. По этой причине в теплотехнических расчетах тепловой поток относится к единице длины цилиндрической стенки:

Где (рь — линейная плотность теплового потока; iLCT = In~ — терми-

27ГА di

Ческое сопротивление цилиндрической стенки, м2 — К/Вт.

Определить термическое сопротивление цилиндрической стенки доста­точно сложно, поэтому для приближенного расчета его часто определяют по более простой формуле плоской стенки:

R = 6/ А.

Чем меньше отношение диаметров d2/di, тем меньше ошибка в вычис­лении термического сопротивления по упрощенной формуле. Установлено, что при отношении rf2/di = 2 формула (14.13) дает ошибку, равную 4%, а при rf2/di = 1.5 ошибка уменьшается до 1.4%.

Обычно в трубчатых теплообменных аппаратах, в цилиндрах двигате­лей внутреннего сгорания отношение диаметров не превышает 1.5, поэтому при расчете теплопроводности в этих случаях можно пользоваться форму­лами для плоской стенки.

Количество теплоты, прошедшее через цилиндрическую стенку длиной L за t секунд, определяется как обычно:

Q = *t, Щж]. (14.14)

Поток энергии в тепловой форме

Ь3 ь2 Bj

Ь2 Ьз

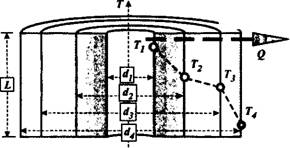
Рис. 14.5. К определению теплопроводности трехслойной цилиндрической стенки

Для трехслойной цилиндрической стенки (рис. 14.5) на основании вы­ражения (14.13) можно записать:

In — ln^ In —

D\ da

Решая эти уравнения относительно разностей температур, а затем, почленно складывая, получим

4>l ( 1 , d2 , 1 , d3 , 1 , dA

1 4 27Г (Ai d\ A3 da A3

Отсюда

2Ж • (Тх — T4) VL J-ln^ + J-ln^ + i-ln^i"

Ai D\ Aa D2 A3 d3

Обобщая формулу (14.15) на n-слойную стенку, найдем

(14.15) (14.16)

_ 2п • (Тх — Tn+I)

А< di

Где i — порядковый номер слоя.

Уравнение Ньютона-Рихмана

Закон Нью́тона — Ри́хмана — эмпирическая закономерность, выражающая тепловой поток между разными телами через температурный напор

10.2. Закон Ньютона-РихманаПроцесс теплообмена между поверхностью тела и средой описывается законом Ньютона-Рихмана, которая гласит, что количество теплоты, передаваемая конвективным теплообменом прямо пропорционально разности температур поверхности тела (t'ст)и окружающей среды (t'ж):Q = α · (t'ст - t'ж)·F , (10.1)илиq = α · (t'ст - t'ж) , (10.2)где: коэффициент теплоотдачи [Вт/(м2К)], характеризует интенсивность теплообмена между поверхностью тела и окружающей средой.

Факторы, которые влияют на процесс конвективного теплообмена, включают в этот коэффициент теплоотдачи. Тогда коэффициент теплоотдачи является функцией этих параметров и можно записать эту зависимость в виде следующего уравнения:α = f1(Х; Ф; lo; xc; yc; zc; wo; θ; λ; а; ср; ρ; ν; β) , (10.3)где: Х – характер движения среды (свободная, вынужденная);

Ф – форма поверхности;

lo – характерный размер поверхности (длина, высота, диаметр и т.д.);

xc; yc; zc – координаты;

wo – скорость среды (жидкость, газ);

θ = (t'ст - t'ж) – температурный напор;

λ – коэффициент теплопроводности среды;

а – коэффициент температуропроводности среды;

ср –изобарная удельная теплоемкость среды;

ρ –плотность среды;

ν – коэффициент кинематической вязкости среды;

β – температурный коэффициент объемного расширения среды.

Уравнение (10.3) показывает, что коэффициент теплоотдачи величина сложная и для её определения невозможно дать общую формулу. Поэтому для определения коэффициента теплоотдачи применяют экспериментальный метод исследования.

Достоинством экспериментального метода является: достоверность получаемых результатов; основное внимание можно сосредоточить на изучении величин, представляющих наибольший практический интерес.

Основным недостатком этого метода является, что результаты данного эксперимента не могут быть использованы, применительно к другому явлению, которое в деталях отличается от изученного. Поэтому выводы, сделанные на основании анализа результатов данного экспериментального исследования, не допускают распространения их на другие явления. Следовательно, при экспериментальном методе исследования каждый конкретный случай должен служить самостоятельным объектом изучения.