Политропные процессы идеального газа. Уравнение процесса. Показатель политропы. Изображение на диграммах

1. Политропный процесс. 1.1. Уравнение процесса. В лекции 2 довольно кратко уже говорилось о политропе, теперь – подробнее. Уравнение политропического процесса имеет вид: pvn = const, n = const. Но это не единственная форма связи параметров состояния, возможны комбинации: pTn΄ = const, n΄ = const или vTn΄΄= const, n΄΄= const. Далее, для примера, будем работать с уравнением pvn = const, n = const. На практике показатель политропы n находят экспериментально следующим образом: pvn = const → lnp + nlnv = const → lnp = - nlnv + const. Последнее выражение представляет собой уравнение прямой линии в координатах lnp – lnv. В эксперименте с каким-то веществом для различных условий измеряют давление р и удельный объем v с какой-то инструментальной точностью. Далее строят график в осях lnp – lnv (см. рис. 3. 1) и по нему находят показатель политропы n. Рис. 3. 1. Иллюстрация к экспериментальному определению показателя политропы n – индикаторная диаграмма в логарифмических координатах. n = - tgα. · - обозначение экспериментальных точек. Истоки вывода уравнения pvn = const уходят в анализ работы реальных поршневых машин (паровых и компрессоров). При анализе их работы снимали индикаторную диаграмму p = f(x), где х – ход поршня. От индикаторной диаграммы всего один шаг до p – v диаграммы. Показатель политропы n в уравнении pvn = const в сущности отражает интенсивность изменения параметров в процессе, т.е. характер смены состояний. А параметры изменяются под влиянием внешних воздействий q и w на термодеформационную систему. Поэтому мы в праве ожидать, что n = n(q,w). Проверим это ожидание. Исходное уравнение политропы pvn = const в логарифмической форме lnp = -nlnv + const после дифференцирования принимает вид: dp/p = -n dv/v или n = -vdp/pdv (3.1) Иными словами: показатель политропы n есть отношение элементарной работы проталкивания к элементарной работе деформации (сжатия или расширения), и наши ожидания подтвердились. Далее, вспомним первый закон термодинамики в форме du = dq – dw → du = dq – pdv → pdv = dq – du; (3.2.1) dh = dq +dw΄ → dh = dq +vdp → vdp = dh – dq; (3.2.2) Подстановка (3.2.1) и (3.2.2) в (3.1) дает результат: n = (dq – dh) / (dq –du). (3.3) В лекции 2 подробно рассматривалось понятие теплоемкости и было показано, что dq = cdT. Одновременно, для идеального газа и любого процесса были получены связи du = cvdT и dh = cpdT. Тогда зависимость (3.3) для идеального газа принимает вид: n = (cdT – cpdT) / (cdT – cvdT) = (c – cp)/(c – cv). (3.4) Следовательно, показатель политропы n для идеального газа получил вполне определенный смысл – это функция теплоемкостей. Из (3.4) попутно получим зависимость истинной политропной теплоемкости сn от показателя политропы n , чтобы можно было рассчитывать количество теплоты так, как это принято в калориметрии dq = cndT. Действительно (см. (3.4)), c ≡ cn = (ncv –cp) / (n – 1) = cv (n – k) / (n – 1). (3.5) В (3.5) величина k ≡ ср/сv носит название коэффициента Пуассона и является показателем адиабаты. Для двухатомных газов k ≈ 1,4. Так как n = const и k = const, то (3.5) справедливо и для средней политропной теплоемкости: cn|t1 t2 = cv|t1 t2 (n – k) / (n – 1), k = cp|t1 t2 / cv|t1 t2 . (3.6)

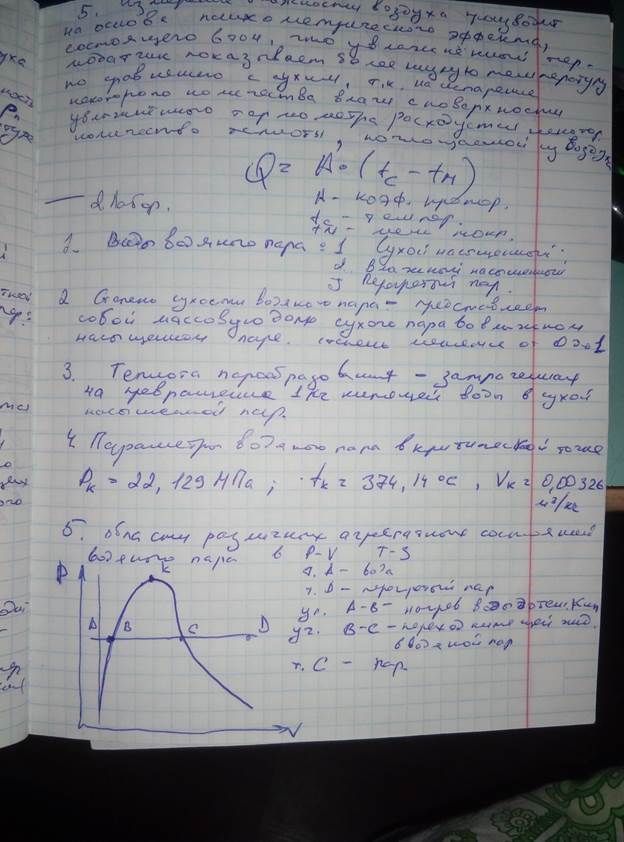
Реальные газы

9. простые и сложные виды теплообмена. стационарный теплообменник

Всего существует три простых (элементарных) механизма передачи тепла:

• Теплопроводность
• Конвекция
• Тепловое излучение

Существуют также различные виды сложного переноса тепла, которые являются сочетанием элементарных видов. Основные из них:

• теплоотдача (конвективный теплообмен между потоками жидкости или газа и поверхностью твёрдого тела);
• теплопередача (теплообмен от горячей среды (жидкость, газ или твердое тело) к холодной через разделяющую их стенку);
• конвективно-лучистый перенос тепла (совместный перенос тепла излучением и конвекцией);
• термомагнитная конвекция

Внутренние источники теплоты - понятие теории теплопередачи, которое описывает процесс производства (реже поглощения) тепловой энергии внутри материальных тел без какого-либо подвода или переноса тепловой энергии извне. К внутренним источникам теплоты относятся:

• тепловыделение при работе электрического тока
• тепловыделение при ядерных реакциях
• тепловыделение при химических реакциях

Рекуперат́ивный теплообме́нник — теплообменник, в котором горячий и холодный теплоносители движутся в разных каналах, теплообмен происходит через стенку. При этом тепловой поток в каждой точке стенки сохраняет одно и то же направление. Если параметры теплоносителей на входах в теплообменник не изменяются, то при ламинарных течениях внутри параметры теплоносителей будут независимы от времени. В этом случае, процесс теплопередачи имеет стационарный характер, и такие теплообменники называют также стационарными, в противоположность, например, от регенеративных теплообменников.^[1]

В зависимости от направления движения теплоносителей рекуперативные теплообменники могут быть прямоточными при параллельном движении в одном направлении, противоточными при параллельном встречном движении, а также перекрестноточными при взаимно перпендикулярном движении двух взаимодействующих сред