Случай прямоугольной области

Пусть дана функция двух переменных f(x, y) и ограничения для D: D = {(x; y) | a ≤ x ≤ b; c ≤ y ≤ d}, означающие, что фигуру D слева и справа ограничивают прямые x = a и x = b, а снизу и сверху - прямые y = c и y = d. Здесь a, b, c, d - числа.

Пусть для такой функции существует двойной интеграл

.

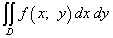Чтобы вычислить этот двойной интеграл, нужно свести его к повторному интегралу, который имеет вид

.

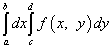Здесь пределы интегрирования a, b, c, d - числа, о которых только что упоминалось.

Сначала нужно вычислять внутренний (правый) определённый интеграл, затем - внешний (левый) определённый интеграл.

Можно и поменять ролями x и y. Тогда повторный интеграл будет иметь вид

.

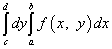Такой повторный интеграл нужно решать точно так же: сначала - внутренний (правый) интеграл, затем - внешний (левый).

24)
Пусть снова дана функция двух переменных f(x, y), а ограничения для D: уже несколько другого вида:

.

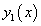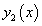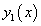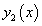Эта запись означает, что фигуру D слева и справа ограничивают, как и в случае прямолинейной области - прямые x = a и x = b, но снизу и сверху - кривые, которые заданы уравнениями и . Иными словами, и - функции.

Пусть для такой функции также существует двойной интеграл

.

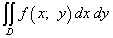Чтобы вычислить этот двойной интеграл, нужно свести его к повторному интегралу, который имеет вид

.

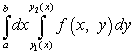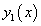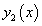Здесь пределы интегрирования a и b - числа, а и - функции. В случае треугольной области одна из функци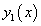й или 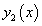- это уравнение прямой линии. Такой случай будет разобран в примере 3.

Как и в случае прямолинейной области, сначала нужно вычислять правый определённый интеграл, затем - левый определённый интеграл.

Точно так же можно поменять ролями x и y. Тогда повторный интеграл будет иметь вид

.

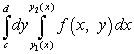Такой повторный интеграл нужно решать точно так же: сначала - внутренний (правый) интеграл, затем - внешний (левый).

25)

26)

27) Тройным интегралом от функции f(x, y, z) по области V называется конечный предел трехмерной интегральной суммы при стремлении к нулю ранга разбиения, порождающего эту сумму (если этот предел существует и не зависит ни от способа разбиения области V на элементарные части, ни от выбора точек на каждой из этих элементарных частей):

Свойство 1 (линейность тройного интеграла по подынтегральной функции)

,

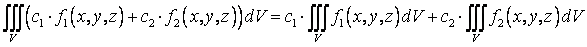где 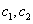— постоянные множители по x, y, z.

Свойство 2 (аддитивность тройного интеграла по области интегрирования)

Если V = V₁ È V₂, то .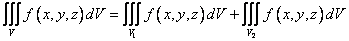

Свойство 3 (о значении тройного интеграла от функции, тождественно равной единице)

Если подынтегральная функция f(x,y,z) º 1 для 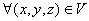, то тройной интеграл от неё по области V равен объему (мере) области интегрирования:

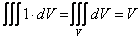
(здесь область V и её объём V обозначены одной буквой).

Свойство 4 (оценки значения тройного интеграла)

Если m и M — наименьшее и наибольшее значения функции f(x,y,z) в замкнутой области V, то

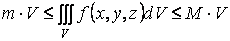
Если |f(x,y,z)| 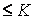при "(x,y,z)ÎV, то

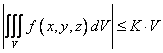
Свойство 5 (теорема о среднем значении подынтегральной функции)

Если функция f (x,y,z) непрерывна в области V, то существует хотя бы одна точка P₀(x₀;y₀;z0)ÎV такая, что

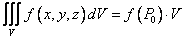
При этом число 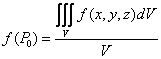называется средним значением

функции f(x,y,z) по области V.

28) Вычисление тройного интеграла сводится к вычислению трехкратного интеграла.
В декартовых координатах область V, правильная в направлении оси OZ, записывается системой неравенств

,

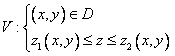где D – это проекция области V на плоскость XOY, а поверхност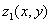и и 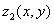ограничивают область V соответственно снизу и сверху (Рис. 6).

Если двумерную область D также записать системой неравенств 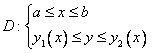, то трехмерная область V запишется системой трех неравенств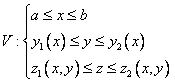

Тогда тройной интеграл сводится сначала к двойному, а затем к трёхкратному с учётом того, что в декартовых координатах dV = dx×dy×dz;

формула сведения тройного интеграла к трехкратному интегралу имеет следующий вид:

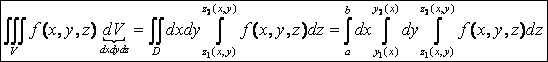29) Замена переменных в тройном интеграле 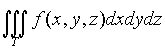состоит в переходе от переменных x, y, z к новым переменным u, v, w по формулам

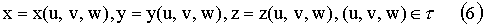
Если выполняются условия

1?. Отображение (6) взаимно однозначно;

2?. Функции в (6) непрерывно - дифференцируемы в области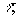

3?. Якобиан отображения

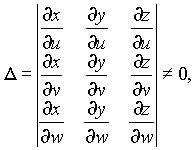
то имеет место формула

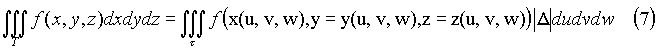
Цилиндрические координаты представляют соединение полярных координат в плоскости xy с обычной декартовой аппликатой z (рис. 3).

Пусть M(x, y, z) - произвольная точка в пространстве xyz, P - проекция точки M на плоскость xy. Точка M однозначно определяется тройкой чисел 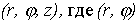- полярные координаты точки P, z - аппликата точки M. Формулы, связывающие их с декартовыми, имеют вид

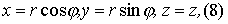
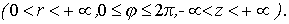
30) Сферические координаты.Пусть M(x, y) - произвольная точка в пространстве xyz, P - проекция точки M на плоскость xy. Точка M однозначно задаётся тройкой чисел 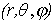, где r - расстояние точки M до точки 0, 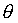- угол между лучами OM и OZ, 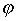- полярный угол точки P на плоскости xy. Тройка чисел 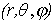называется сферическими координатами точки M.

Они связаны с прямоугольными формулами

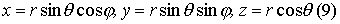
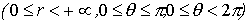
Якобиан отображения 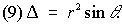. Иногда используются обобщённые сферические координаты.

Объём V кубируемой области T (кубического тела) в пространстве xyz выражается формулой

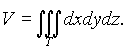
31) 1. Вычисление объемов тел с помощью двойного интеграла.

1.1. Пусть 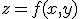-неотрицательная, непрерывная функция в замкнутой области 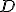. Если 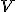- тело, ограниченное сверху поверхностью 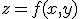, снизу - областью 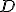, а сбоку - соответствующей цилиндрической поверхностью с образующей параллельной оси OZ и направляющей, совпадающей с границей области 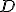, то объем этого тела равен

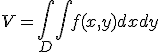(1)

1.2. Пусть 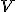- тело, ограниченное сверху поверхностью 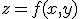, снизу - поверхностью 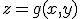, причем проекцией обеих поверхностей на плоскость 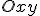служит область 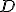, в которой функци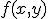и и 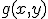непрерывны (и 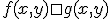), то объем этого тела равен

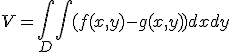(2)