Электростатика. постоянный ток

3.1.Закон Кулона

,

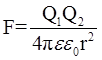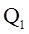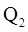где F – сила взаимодействия точечных зарядов и ; r– расстояние между зарядами; 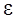– диэлектрическая проницаемость среды; 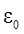– электрическая постоянная.

3.2.Напряженность электрического поля 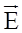и сила 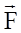, действующая на точечный заряд, находящийся в электрическом поле

; .

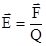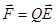3.3. Напряженность Е и потенциал поля φ, создаваемого точечным зарядом:

; ,

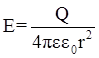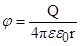где r - расстояние от заряда до точки, в которой определяется напряженность и потенциал (при условии, что потенциал в точке, удаленной в бесконечность, равен нулю).

3.4.Напряженность и потенциал поля, создаваемого системой точечных зарядов (принцип суперпозиции электрических полей)

; ,

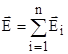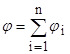где 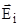и φ_i - соответственно напряженность и потенциал в данной точке поля, создаваемого i–м разрядом.

3.5. Напряженность поля, создаваемого равномерно заряженной линией

,

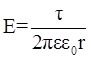где 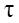- линейная плотность заряда, т.е. величина заряда, приходящего на единицу длины нити l (τ = Q/l); r – расстояние от нити до точки, в которой вычисляется напряженность поля.

3.6. Напряженность поля равномерно заряженной плоскости и плоского конденсатора соответственно

; ,

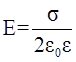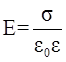где 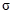- поверхностная плотность заряда, т.е. величина заряда, приходящегося на единицу площади поверхности S ( 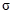=Q/S).

3.7. Связь потенциала с напряженностью

а) для однородного поля (например, поля, создаваемого равномерно заряженной плоскостью):

;

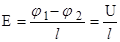где φ₁ – φ₂ - разность потенциалов в двух точках, стоящих друг от друга на расстоянии l вдоль силовой линии;

б) для поля, обладающего центральной симметрией (например, поле заряженной прямой линией):

;

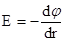где r – расстояние вдоль силовой линии.

3.8. Работа кулоновских сил по перемещению заряда (Q) из точки поля потенциалаφ₁в точку поля с потенциаломφ₂

A=Q(φ₁ – φ₂).

3.9. Электроемкость

а) уединенного проводника:

,

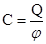где Q – заряд проводника, φ - потенциал проводника (при условии, что в бесконечности потенциал проводника принимается равным нулю);

б) конденсатора (совокупность двух проводников):

;

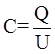где U - разность потенциалов проводников, составляющих конденсатор.

3.10. Электроемкость плоского конденсатора

;

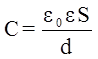где S – площадь пластины (одной) конденсатора; d – расстояние между пластинами.

3.11. Электроемкость батареи конденсаторов

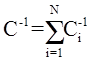(при последовательном соединении);

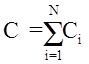(при параллельном соединении),

где N – число конденсаторов в батарее.

3.12. Энергия заряженного конденсатора

.

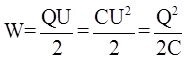3.13. Сила постоянного тока

,

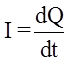где dQ – заряд, прошедший через сечение проводника за время dt.

3.14.Плотность тока

,

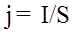где S – площадь поперечного сечения проводника.

3.15. Связь плотности тока со средней скоростью < и > направленного движения заряженных частиц

,

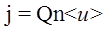где n – концентрация заряженных частиц.

3.16.Закон Ома в дифференциальной форме

j = γE = E/ρ,

где γ- удельная проводимость, Е – напряженность электрического поля, ρ – удельное сопротивление.

3.17. Связь удельной проводимости с подвижностью ионов (заряженных частиц)

,

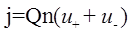где Q – заряд ионов, n – концентрация ионов, 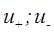- подвижности положительных и отрицательных ионов соответственно.

3.18. Закон Ома:

a) 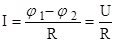- для участка цепи, не содержащего ЭДС,

где φ₁ – φ₂ =U - разность потенциалов (напряжение) на концах участка цепи; R – сопротивление участка;

б) 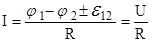- для участка цепи, содержащего ЭДС,

где ε₁₂ - ЭДС источника тока; R₁₂ - полное сопротивление участка (сумма внешних и внутренних сопротивлений);

в) 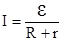- для замкнутой цепи,

где R – внешнее сопротивление цепи, r – внутреннее сопротивление.

3.19. Законы Кирхгофа

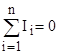- для узлов;

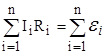- для контуров.

3.20. Сопротивление R и проводимость G проводника

; ,

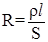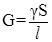где ρ – удельное сопротивление; γ - удельная проводимость; l - длина проводника; S – площадь поперечного сечения.

3.21. Сопротивление системы проводников

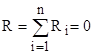- при последовательном соединении;

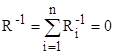- при параллельном соединении,

где 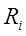- сопротивление i–го проводника.

3.22. Работа тока

.

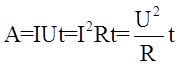3.23. Мощность тока

.

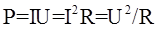3.24. Закон Джоуля - Ленца

;

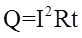3.25.Закон Фарадея для электролиза

;

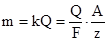где F – число Фарадея; А – атомная масса; Z – валентность.

ЭЛЕКТРОМАГНИТНЫЕ ЯВЛЕНИЯ

И КВАНТОВЫЕ ЭФФЕКТЫ

Основные формулы

4.1.Связь магнитной индукции 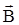с напряженностью 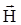магнитного поля

,

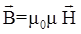где μ₀ - магнитная постоянная; μ - магнитная проницаемость среды (μ = 1 для вакуума, μ ≈ 1 для воздуха).

4.2.Магнитная индукция поля прямого тока

,

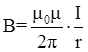где r – расстояние от оси проводника до точки, в которой определяется магнитная индукция.

4.3. Магнитная индукция поля соленоида

,

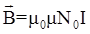где N₀ - отношение числа векторов соленоида к его длине.

4.4. Сила, действующая на проводник с током в магнитном поле (Закон Ампера)

,

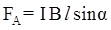где l - длина проводника; α - угол между направлениями тока в проводнике и вектором магнитной индукции.

4.5. Магнитный момент плоского контура с током

,

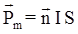где 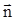- единичный вектор нормали (положительной) к плоскости контура; I – сила тока, протекающего по контуру; S – площадь контура.

4.6. Механический (вращательный) момент, действующий на контур с током, помещенный в однородное магнитное поле

;

,

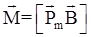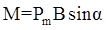где α - угол между векторами .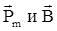

4.7. Магнитный поток (в случаи однородного магнитного поля и плоской поверхности)

;

,

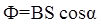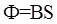где S – площадь контура; α – угол между нормалью к плоскости контура и вектором магнитной индукции.

4.8. Работа по перемещению замкнутого контура в магнитном поле

,

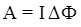где ΔФ – изменение магнитного потока.

4.9. Электродвижущая сила индукции

,

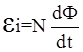где N – число витков в контуре.

4.10. Сила Лоренца

;

,

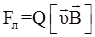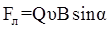где υ - скорость заряженной частицы; α – угол между векторами .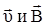

4.11. Формула Томсона для периода колебания в колебательном контуре

,

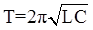где L – индуктивность контура, С – емкость контура.

4.12. Связь между длинной волны и скоростью ее распространения

;

,

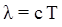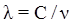где ν – частота колебаний, с – скорость электромагнитной волны в вакууме (С =3·10⁸ м/с).

4.13. Энергия фотона

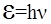
где h – постоянная планка, ν - частота фотона.

4.14. Формула Эйнштейна для фотоэффекта

,

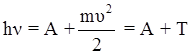где А – работа выхода электрона; Т – максимальная кинетическая энергия фотоэлектрона.