В дальнейшем будем рассматривать изменения состояния только этой части воздуха.

Процесс А → В → 1. Состояние 1.

Для того чтобы перевести газ М₀ из состояния А в состояние 1

(т.е. уменьшить его объём), с помощью компрессора через напускной кран К₁ (см. рис. 2) в баллон нагнетается некоторое количество m воздуха. Эта часть воздуха (ее можно назвать рабочей массой или рабочим телом) играет роль своеобразного «сплошного поршня», заполняющего часть объёма баллона. По окончании этого процесса кран К1 переводят в положение «Закрыто».

При вводе в баллон рабочего массы газа внешние силы совершают над газом М0 и mположительную работу, что приводит к увеличению внутренней энергии системы (давления и температуры в ней). Новое состояние воздуха описать сложно, так как возникающий теплообмен между газом в баллоне и стенками баллона (между баллоном и атмосферным воздухом) приводит к обратному эффекту. Таким образом, значения температуры и давления в системе, при завершении нагнетания рабочего массы газа m, определяются скоростью нагнетания. С этой точки зрения, процесс нагнетания можно осуществить одним из следующих способов.

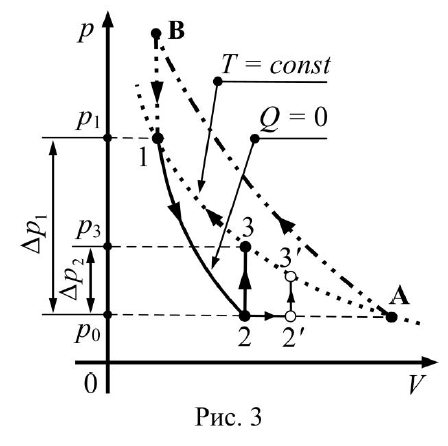
Первый - это способ «быстрого» нагнетания (процесс А → В на рис. 3). При завершении этого процесса кран К₁ переводится в положение «Закрыто» и воздух в баллоне начинает изохорно остывать (процесс В → 1 на рис. 3) до температуры окружающей среды (T₁ = Т₀), при этом его давление уменьшится до величины p₁ > р₀ и уровень жидкости в коленах манометра перестанет

меняться. Давление р₁, в соответствии с (1), можно определить из соотношения

где Н = H₁ - Н₂ - разность уровней воды в коленах манометра.

Второй способ перевода газа М₀ из состояния А в состояние 1 - это способ квазистатического изотермического нагнетания (процесс А → 1). При осуществлении такого процесса воздух в баллоне все время находится в тепловом и механическом равновесии с окружающей средой.

Таким образом, в состоянии 1 воздух М₀ характеризуется следующими параметрами: p₁ > p₀, T₁ = T₀, V₁ < V₀.

Процесс 1 → 2. Состояние 2.

Для осуществления процесса 1 → 2 воздух в баллоне с помощью крана К₂ (см. рис. 2) кратковременно соединяют с атмосферой. При этом часть рабочей массы воздуха mвыпускается в атмосферу и давление в баллоне падает до значения р₂, равного атмосферному (p₂ = p₀). Между газом в баллоне и атмосферой устанавливается механическое равновесие. С другой стороны, при выводе части рабочего тела из системы, газ в баллоне совершает положительную работу против сил внешнего давления (процесс 1 → 2), что приводит к понижению температуры системы до величины Т₂.

Таким образом, воздух М₀ в состоянии 2 характеризуется следующими параметрами: p₂ = p₀, Т₂ < T₀, V₁ < V₂ < V₀.

Очевидно, что длительность процесса l → 2 и его вид зависят как от величины избыточного давления ∆p_l = pgH, так и от сечении выпускного крана К₂. В методе Клемана и Дезорма этот процесс считается адиабатическим. Это возможно, если ∆р₁ << р₀, а также если сечение выпускного крана К₂ достаточно велико. Только в этом случае процесс 1 → 2 произойдёт достаточно быстро, так, что можно пренебречь теплообменом между газом в баллоне и окружающей средой. В лабораторной установке длительность этого процесса составляет ∆τ₂ ≈ 0,1 с. Для сравнения, одно моргание человеческого глаза длится приблизительно 0,05 секунды.

Процесс 2 → 3. Состояние 3.

Допустим, что в конце адиабатического процесса 1 → 2 кран сброса воздуха К₂ закрывается. Далее воздух в баллоне начнёт изохорически медленно нагреваться (процесс 2 → 3) до температуры окружающей среды (T₃ = Т₀), при этом его давление возрастет до величины р₃ > р₀ и уровень жидкости в коленах манометра перестанет меняться. В соответствии с (1) давление воздуха в баллоне р₃ можно определить из соотношения

где h = h₁ - h₂ - разность уровней воды в коленах манометра.

Таким образом, в состоянии 3 газ М₀ находится в тепловом и механическом равновесии с окружающей средой и характеризуется следующими параметрами: р₃ > р₀, T₃ = T₀, V₃ = V₂ < V₀.

Используя описанный выше процесс 1 → 2 → 3, законы идеального газа и уравнение адиабатического процесса, выведем расчетную формулу для определения величины γ.

Давление и температура воздуха М₀ в процессе 1 → 2 → 3 (см. рис. 3) связаны следующими соотношениями:

адиабатический процесс 1 → 2:

изохорический процесс 2 → 3:

Решая совместно (4) и (5), получим следующее уравнение:

В лабораторной установке манометр позволяет измерить величину избыточного давления воздуха в баллоне. Поэтому в уравнение (6) следует подставить соотношения (2) и (3):

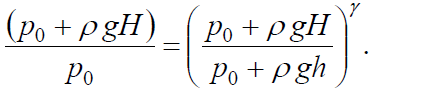
После логарифмирования этого равенства и простых математических преобразований получаем следующее соотношение для показателя адиабаты γ воздуха:

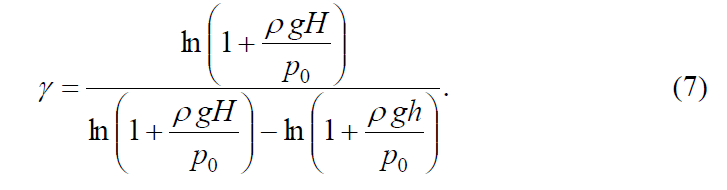
В вышеописанном методе предполагается, что атмосферное давление р₀ много больше избыточного давления, т.е. р₀ >> pgH и pgh. Тогда можно принять что ln(1+x) ≈ х (первый член в разложении соотношения ln (1 + х) в ряд Маклорена), где х это (pgH)/p₀ и pgh/p₀. С учетом этого из (7) получаем следующую простую формулу для определения показателя адиабаты воздуха:

Учитывая, что H = H₁ - H₂, а h = h₁ - h₂, окончательно получаем рабочую формулу для расчета показателя адиабаты воздуха:

В формуле (8) под величиной h понимается разность уровней воды в коленах манометра, возникающая в предположении, что кран К₂ закрывается в момент окончания адиабатического расширения 1 → 2 (см. рис. 3).

Если кран К₂ закрыть спустя некоторое время после завершения процесса 1 → 2, то за это время температура в баллоне изобарно повысится (процесс 2 → 2' на рис. 3). В этом случае соответствующая разность высот (H - h) увеличится, что приведет к уменьшению значения у Если же кран закрыть до завершения этого процесса, то разность высот (H - h) уменьшается, что приводит к увеличению величины у по сравнению с ее действительным значением.

Таким образом, для получения «хороших» результатов выпускной кран К2 необходимо закрыть в момент окончания адиабатного процесса 1 → 2.