Физические свойства жидкости
Жидкость. Основные понятия.физические свойства
Жидкость представляет собой физическое тело, в котором силы межмолекулярного сцепления меньше, чем у твердых тел. Поэтому частицы жидкости легкоподвижны и приобретают как поступательное, так и вращательное движение, различают капельные и газообразные жидкости. Капельные жидкости характеризуются большим сопротивлением сжатию, практически полной несжимаемостью, малым сопротивлением растягивающим и касательным усилиям, что обусловлено незначительностью сил сцепления и сил трения между частицами жидкости и незначительной температурной расширяемостью. К капельным жидкостям относят воду, нефть, глицерин, бензин, спирт и т. д. Газообразные жидкости изменяют свой объем под влиянием указанных факторов в значительной степени, поэтому в гидравлике рассматривают обычно капельные жидкости, а газообразные рассматриваются в термодинамике и аэродинамике. При изменении давления или температуры жидкое тело может переходить в твердое или газообразное.
Таким образом, жидкость есть физическое тело, обладающее двумя отличительными свойствами:
1. Она весьма мало изменяет свой объем при изменении давления или температуры (сходна в этом с твердыми телами).
2. Она обладает текучестью, благодаря чему жидкость не имеет собственной формы и принимает форму того сосуда, в который она помещена (в этом она сходна с газом).
Жидкость настолько подвижна, что может течь под действием силы тяжести. Текучесть обусловлена тем, что в покоящемся состоянии она не способна сопротивляться внутренним касательным усилиям. Жидкость в покое не может иметь касательных напряжений и поэтому принимает форму сосуда, в который заключена.
Как показывает опыт, жидкости, встречающиеся в природе, столь мало изменяют объем при изменении давления р и температуры Т, что этим изменением можно пренебречь и рассматривать ее как абсолютно несжимаемое тело. В газах же этими свойствами пренебрегать нельзя.
В движущейся жидкости касательные напряжения имеют место. Именно при движении по поверхности скольжения жидких слоев друг по другу возникает трение, которое уравновешивает внутренние касательные силы.
Свойство жидкости, обусловливающее возникновение в ней при движении касательных напряжении, называется вязкостью.
При аналитических исследованиях для облегчения решения многих задач гидравлики часто пользуются понятием идеальной жидкости. Идеальной жидкостью называют воображаемую жидкость, которая характеризуется:
- абсолютной неизменяемостью объема при изменении давления или температуры (абсолютно несжимаемое тело);
- абсолютной подвижностью частиц, т. е. полным отсутствием вязкости, сил трения при ее движении.
Идеальная жидкость в отличие от реальной жидкости в природе не существует. Ее создают в воображении как чисто отвлеченную модель жидкой среды.
Но рассматривая вместо реальной жидкости идеальную, мы в ряде случаев не делаем большой ошибки. Только пренебрежение вязкостью может дать более или менее существенное расхождение с действительными условиями.
Число Рейнольдса
Режим движения жидкости в трубе изменяется примерно при определенной средней по сечению скорости 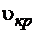 , которую называют критической. Значение этой скорости прямо пропорционально кинематической вязкости и обратно пропорционально диаметру трубы:
, которую называют критической. Значение этой скорости прямо пропорционально кинематической вязкости и обратно пропорционально диаметру трубы:
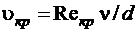 .
.
Входящий в эту формулу безразмерный коэффициент пропорциональности 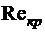 (критическое число Рейнольдса) одинаков для всех жидкостей и газов, а также для любых диаметров труб. Это означает, что изменение режима течения происходит при определенном соотношении между скоростью, диаметром и кинематической вязкостью:
(критическое число Рейнольдса) одинаков для всех жидкостей и газов, а также для любых диаметров труб. Это означает, что изменение режима течения происходит при определенном соотношении между скоростью, диаметром и кинематической вязкостью:
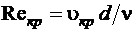 . (1.5.1)
. (1.5.1)
для труб круглого сечения 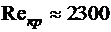 .
.
С физической точки зрения, критерий Рейнольдса 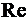 есть отношение сил инерции потока к силам трения при движении жидкости.
есть отношение сил инерции потока к силам трения при движении жидкости.
При 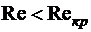 движение жидкости является ламинарным, при
движение жидкости является ламинарным, при 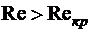 - турбулентным.
- турбулентным.
В гидравлических приводах технологического оборудования устойчивое турбулентное течение жидкости в трубах наблюдается при 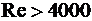 , а при
, а при 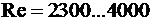 имеет место переходная, критическая область, в которой в разные периоды времени возможен ламинарный или турбулентный режим движения. Это объясняется тем, что на практике обычно имеются причины, способствующие турбулизации потока жидкости: вибрация труб и других гидравлических устройств, местные гидравлические сопротивления, неравномерность (пульсация) подачи объемных насосов и др.
имеет место переходная, критическая область, в которой в разные периоды времени возможен ламинарный или турбулентный режим движения. Это объясняется тем, что на практике обычно имеются причины, способствующие турбулизации потока жидкости: вибрация труб и других гидравлических устройств, местные гидравлические сопротивления, неравномерность (пульсация) подачи объемных насосов и др.
В приводах технологического оборудования, в которых в качестве рабочей жидкости используют минеральные масла, турбулентный режим возникает при скоростях более 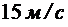 , тогда как при проектировании предусматривают скорости до
, тогда как при проектировании предусматривают скорости до 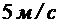 . Режим движения в таких трубопроводах, как правило, ламинарный.
. Режим движения в таких трубопроводах, как правило, ламинарный.
Для труб и каналов некруглой формы характерным линейным размером является гидравлический радиус 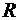 , определяемый соотношением (1.3.1), тогда число Рейнольдса для любой формы поперечного сечения потока, в том числе для случая безнапорного движения, можно определить по формуле
, определяемый соотношением (1.3.1), тогда число Рейнольдса для любой формы поперечного сечения потока, в том числе для случая безнапорного движения, можно определить по формуле
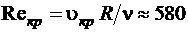 .
.
Режим движения жидкости оказывает существенное влияние на гидравлическое сопротивление и потери давления. Так, потери давления по длине трубы при ламинарном режиме движения пропорциональны средней скорости течения в первой степени, а при турбулентном режиме – в степени 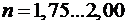 . С увеличением числа Рейнольдса показатель степени увеличивается, достигая максимального значения
. С увеличением числа Рейнольдса показатель степени увеличивается, достигая максимального значения 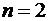 (рис. 1.5.1).
(рис. 1.5.1).
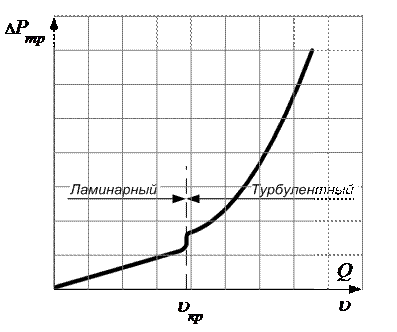 |
Рис. 1.5.1. Зависимость потерь давления 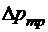 на преодоление сил жидкостного трения по длине трубы от скорости на преодоление сил жидкостного трения по длине трубы от скорости 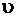 и объемного расхода и объемного расхода 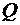 жидкости жидкости |
Следовательно, при определении потерь давления надо знать вид движения жидкости и затем уже выбирать соответствующую формулу для расчета.
Ударное давление
Разновидности гидроудара
Теоретическое и экспериментальное исследованиегидравлического удара в трубопроводах впервые было проведено известным русским учёным Николаем Егоровичем Жуковским в 1899 году. Это явление связано с тем, что при быстром закрытии трубопровода, по которому течёт жидкость, или быстром его открытии (т.е. соединении тупикового трубопровода с источником гидравлической энергии) возникает резкое, неодновременное по длине трубопровода изменение скорости и давления жидкости. Если в таком трубопроводе измерять скорость жидкости и давление, то обнаружится, что скорость меняется как по величине, так и по направлению, а давление - как в сторону увеличения, так и в сторону уменьшения по отношению к начальному. Это означает, что в трубопроводе возникает колебательный процесс, характеризующийся периодическим повышением и понижением давления. Такой процесс очень быстротечен и обусловлен упругими деформациями стенок трубы и самой жидкости.
Подробно рассмотрим его картину для случая полногои прямого гидравлич  еского удара.
еского удара.
Будем считать, что в исходном состоянии трубопровод открыт. Жидкость движется по трубе со скоростью V>0. Д  авление в жидкости равноРо.
авление в жидкости равноРо.
Трубопровод мгновенно закрывается. Слои жидкости, натолкнувшись на заслонку крана, останавливаются. Кинетическая энергия жидкости переходит в деформацию стенок трубы (труба у заслонки расширится), и жидкости (давление у заслонки повысится на величину 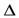 Р). На остановившиеся у заслонки слои жидкости будут набегать следующие, вызывая сжатие жидкости и рост давления, который будет с некоторой скоростью распространяться в сторону противоположную направлению скорости движения жидкости. Переходная область в сечении A-Aназывается ударной волной. Скорость перемещения сечения A-A(фронта волны) называется скоростью распростран
Р). На остановившиеся у заслонки слои жидкости будут набегать следующие, вызывая сжатие жидкости и рост давления, который будет с некоторой скоростью распространяться в сторону противоположную направлению скорости движения жидкости. Переходная область в сечении A-Aназывается ударной волной. Скорость перемещения сечения A-A(фронта волны) называется скоростью распростран  ения ударной волны и обозначается буквойа. Такой процесс проходит в период времени
ения ударной волны и обозначается буквойа. Такой процесс проходит в период времени 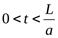 .
.
В момент времени 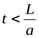 весь трубопровод окажется расширенным, а жидкость сжатой и неподвижной. Но такое состояние неравновесное. Поскольку у источника давление Ро, а в трубе Р = Ро+
весь трубопровод окажется расширенным, а жидкость сжатой и неподвижной. Но такое состояние неравновесное. Поскольку у источника давление Ро, а в трубе Р = Ро+ 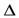 Р, то жидкость начнёт двигаться в сторону меньшего давления, т.е. из трубы в резервуар.
Р, то жидкость начнёт двигаться в сторону меньшего давления, т.е. из трубы в резервуар.
Э 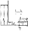 тот процесс начинается от начала трубы. Жидкость будет вытекать из трубы в резервуар с некоторой скоростьюV. Сечение A-A(ударная волна) начнёт перемещаться к концу трубы со скоростью а.При этом давление в трубе будет снижаться до P0.
тот процесс начинается от начала трубы. Жидкость будет вытекать из трубы в резервуар с некоторой скоростьюV. Сечение A-A(ударная волна) начнёт перемещаться к концу трубы со скоростью а.При этом давление в трубе будет снижаться до P0.
Этот процесс будет происходить в период времени 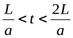 .
.
Э 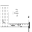 нергия деформации жидкости переходит в кинетическую энергию, и жидкость приобретает некоторую скоростьV, но направленную в обратную сторону. Во всём трубопроводе устанавливается давление Ро. По инерции жидкость продолжает двигаться к началу трубы и начинает испытывать деформации растяжения, что приводит к уменьшению давления вблизи заслонки.
нергия деформации жидкости переходит в кинетическую энергию, и жидкость приобретает некоторую скоростьV, но направленную в обратную сторону. Во всём трубопроводе устанавливается давление Ро. По инерции жидкость продолжает двигаться к началу трубы и начинает испытывать деформации растяжения, что приводит к уменьшению давления вблизи заслонки.
В 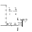
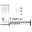 озникает отрицательная ударная волна, движущаяся от конца трубы к началу со скоростьюа, и за фронтом волны остается сжатая труба. Кинетическая энергия снова превращается в энергию деформации (сжатия).
озникает отрицательная ударная волна, движущаяся от конца трубы к началу со скоростьюа, и за фронтом волны остается сжатая труба. Кинетическая энергия снова превращается в энергию деформации (сжатия).
В момент времени 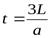 вся труба окажется сжатой, а волна достигает начала трубы. Давление вблизи источника выше, чем во фронте. Из-за этого слои жидкости под действием перепада давления начинают двигаться к концу трубы (к заслонке) с некоторой скоростью V>0, а давление поднимается до Ро.
вся труба окажется сжатой, а волна достигает начала трубы. Давление вблизи источника выше, чем во фронте. Из-за этого слои жидкости под действием перепада давления начинают двигаться к концу трубы (к заслонке) с некоторой скоростью V>0, а давление поднимается до Ро.
П 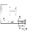 оэтому период времени
оэтому период времени 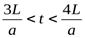 происходит процесс выравнивания давления в трубопроводе. При этом происходит движение ударной волны со скоростью а от начала трубы к её концу.
происходит процесс выравнивания давления в трубопроводе. При этом происходит движение ударной волны со скоростью а от начала трубы к её концу.
В момент времени  ударная волна достигает конца трубы.
ударная волна достигает конца трубы.
Д 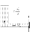 алее весь процесс начинается сначала. При исследовании этого процесса возникает три основных вопроса. Первый - какова скорость протекания этого колебательного процесса и от чего она зависит? Второй вопрос – как сильно меняется давление в трубопроводе за счёт описанного процесса? И третий – как долго может протекать этот процесс?
алее весь процесс начинается сначала. При исследовании этого процесса возникает три основных вопроса. Первый - какова скорость протекания этого колебательного процесса и от чего она зависит? Второй вопрос – как сильно меняется давление в трубопроводе за счёт описанного процесса? И третий – как долго может протекать этот процесс?
Скорость распространения гидравлической ударной волны в трубопроводе
И  зменения давления и скорости потока в трубопроводах происходят не мгновенно в связи с упругостью твёрдых стенок трубы и сжимаемостью рабочей среды, а с некоторой конечной скоростью, обусловленной необходимостью компенсации упругих деформаций жидкости и трубы. Рассмотрим случай когда в трубопроводе длинойL и площадью сечения ωпод давлением Р находится жидкость, плотность которойρ.Предположим, что в момент времени t в сечении 1 – 1 давление повысится на величину dp. Это повышение вызывает увеличение плотности на величину dρ, а также расширение внутреннего диаметра трубы. Следовательно, площадь проходного сечения увеличится на величину dω. В результате увеличится объём W участка трубы на величину dW. За счёт этого произойдет увеличение массы жидкости находящейся в трубе на участке длиной L. Масса увеличится за счёт увеличения, во-первых, плотности жидкости, во-вторых, за счёт увеличения объёма W.
зменения давления и скорости потока в трубопроводах происходят не мгновенно в связи с упругостью твёрдых стенок трубы и сжимаемостью рабочей среды, а с некоторой конечной скоростью, обусловленной необходимостью компенсации упругих деформаций жидкости и трубы. Рассмотрим случай когда в трубопроводе длинойL и площадью сечения ωпод давлением Р находится жидкость, плотность которойρ.Предположим, что в момент времени t в сечении 1 – 1 давление повысится на величину dp. Это повышение вызывает увеличение плотности на величину dρ, а также расширение внутреннего диаметра трубы. Следовательно, площадь проходного сечения увеличится на величину dω. В результате увеличится объём W участка трубы на величину dW. За счёт этого произойдет увеличение массы жидкости находящейся в трубе на участке длиной L. Масса увеличится за счёт увеличения, во-первых, плотности жидкости, во-вторых, за счёт увеличения объёма W.
Такая ситуация рассматривалась при выводе уравнения неразрывности потока в дифференциальной форме, с той только разницей, что там рассматривалось лишь изменение массы во времени, без учёта вызвавших это изменение причин 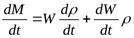 . По аналогии с приведённым уравнением запишем выражение, описывающее изменение массы за счёт изменения давления
. По аналогии с приведённым уравнением запишем выражение, описывающее изменение массы за счёт изменения давления
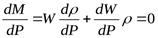 .
.
Жидкость под действием указанного повышения давления устремится с некоторой скоростью а в слои с меньшим давлением, в которых также будет повышаться плотность и увеличиваться напряжение в стенках трубопровода, способствующее увеличению площади трубопровода. В связи с этим потребуется некоторое время на распространение этих деформаций вдоль трубопровода.
С другой стороны, перемещение массы dm за время dtпроисходит под влиянием результирующей Fр сил давления, действующих вдоль линии движения на торцовые поверхности цилиндрического объёма длиной L
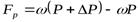
В этом случае уравнение импульса силы может быть представлено в следующем виде
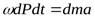 .
.
Отсюда
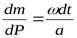 .
.
Имея в виду, что 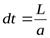 , и подставив это в предыдущее выражение, получим
, и подставив это в предыдущее выражение, получим
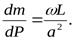
Заметим, что произведение
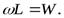
Приравняем оба выражения для 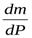 и получим:
и получим:
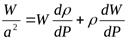 .
.
Выразим из последнего равенства величину a2
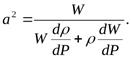
Разделим числитель и знаменатель на W, а первое слагаемое в знаменателе искусственно умножим и разделим на ρ:
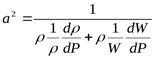 .
.
Обратим внимание на то, что 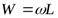 а
а 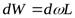 . После подстановки этих равенств в последнее выражение и извлечения корня получим выражение для скорости распространения ударной волны, которая, по сути, является скоростью распространения упругих деформаций жидкости в трубе.
. После подстановки этих равенств в последнее выражение и извлечения корня получим выражение для скорости распространения ударной волны, которая, по сути, является скоростью распространения упругих деформаций жидкости в трубе.
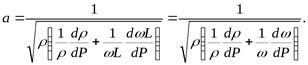
Здесь первое слагаемое под корнем характеризует упругие свойства рабочей среды (жидкости), а – второе упругие силы материала трубы.
Р  ассмотрим подробнее эти слагаемые.
ассмотрим подробнее эти слагаемые.
Как известно из гидростатики, сила, действующая на цилиндрическую поверхность, равна произведению давления на проекцию площади этой поверхности в направлении действия силы. На рассматриваемый участок трубы с толщиной стенок δ, длиной L и диаметром D действует изнутри давление P. Вследствие этого возникает разрывающая сила F, равная
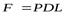 .
.
В стенках трубы возникает сила сопротивления 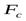 , равная произведению площади сечения стенок трубы
, равная произведению площади сечения стенок трубы 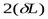 на внутренние напряжения
на внутренние напряжения 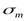 в материале стенок трубы, т.е.
в материале стенок трубы, т.е.
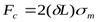 .
.
Если приравнять две эти силы, получим равенство
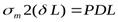 ,
,
из которого найдём выражение, определяющее внутреннее напряжение в стенках трубы 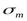 :
:
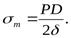
Полагая, что относительное увеличение диаметра трубы, равное 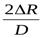 , прямо пропорционально напряжению в стенках трубы, можно записать
, прямо пропорционально напряжению в стенках трубы, можно записать
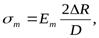
где Ет - коэффициент пропорциональности, который является модулем упругости материала трубы.
Из двух последних выражений следует, что абсолютное приращение радиуса сечения трубы может быть выражено формулой
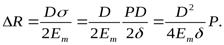
Запишем выражение, определяющее увеличение площади сечения трубы:
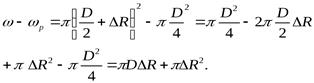
где ω – начальная площадь сечения трубы,
ωр – площадь сечения трубы при давлении P.
Пренебрегая малой величиной высшего порядка ΔR2 и подставив выражение для ΔR, получим
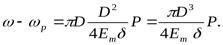
Продифференцировав это выражение по P и рассматривая ω как функцию, зависящую от P, получим:
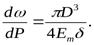
В итоге слагаемое, описывающее упругие свойства материала трубы в выражении для скорости распространения ударной волны, можно представить в следующем виде:
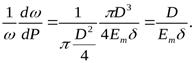
Теперь рассмотрим слагаемое, описывающее упругость жидкости 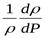 . Ранее при рассмотрении свойств жидкости было установлено, что если изменение объёма происходит за счёт изменения плотности, то можно определить коэффициент сжимаемости жидкостиβw:
. Ранее при рассмотрении свойств жидкости было установлено, что если изменение объёма происходит за счёт изменения плотности, то можно определить коэффициент сжимаемости жидкостиβw:
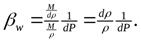
Часто этот коэффициент выражают через обратную величину, называемую модулем упругости жидкости Eж, т. е.:
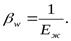
Отсюда следует, что второе слагаемое, характеризующее упругие свойства рабочей среды, может быть представлено в виде:
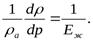
Таким образом, окончательно выражение для скорости распространения ударной волны в упругом трубопроводе можно переписать в следующем виде:
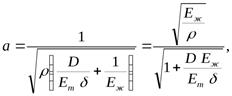
где 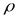 - плотность жидкости,
- плотность жидкости,
D - диаметр трубопровода,
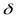 - толщина стенки трубопровода,
- толщина стенки трубопровода,
Ет – объёмный модуль упругости материала трубы,
Еж - объёмный модуль упругости жидкости.
Из формулы следует, что скорость распространения ударной волны зависит от сжимаемости жидкости и упругих деформаций материала трубопровода.
Ударное давление
Для выяснения величины подъёма давления 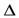 Рприменим теорему о сохранении количества движения (импульса силы). Для этого рассмотрим элементарное перемещение участка жидкости длинной dL за время dt. Учтём, что при прямом гидроударе кинетическая энергия ударной волны полностью превращается в потенциальную, т.е. скорость жидкости V становится равной нулю 0.
Рприменим теорему о сохранении количества движения (импульса силы). Для этого рассмотрим элементарное перемещение участка жидкости длинной dL за время dt. Учтём, что при прямом гидроударе кинетическая энергия ударной волны полностью превращается в потенциальную, т.е. скорость жидкости V становится равной нулю 0.
Импульс силы, под действием которого происходит это движение, равен:
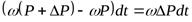 .
.
Изменение количества движения рассматриваемого объёма длиной dL будет:
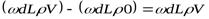 ,
,
Повторимся: скорость во второй скобке равна 0, т.к. рассматриваемый объём жидкости останавливается.
Приравнивая эти выражения по теореме о сохранении количества движения, получим:
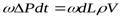 .
.
Отсюда выразим величину повышения давления ΔP:
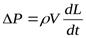 .
.
После замены дроби скоростью a, окончательно будем иметь:
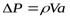 ,
,
где V - скорость жидкости в трубопроводе до возникновения гидроудара,
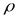 - плотность жидкости,
- плотность жидкости,
а – скорость распространения ударной волны.
Если в эту формулу подставить выражение описывающее a, то придём к формуле, носящей имя Жуковского:
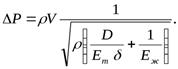
Протекание гидравлического удара во времени
Рассмотренный ранее процесс распространения ударной волны в трубопроводе не происходит бесконечно долго. В опытах Жуковского было зарегистрировано по 12 полных циклов. При этом величина ударного давления ∆P постепенно уменьшалась.
Уменьшение давления вызвано трением в трубе и рассеиванием энергии в резервуаре, обеспечивающем исходный напор. На графике сплошной заштрихованной областью показано теоретическое изменение давления при гидроударе. Прерывистой линией показан примерный вид действительной картины изменения давления.
Разновидности гидроудара
Если трубопровод перекрыть не полностью, то скорость жидкости изменится не до нуля, а до значения V1 . В этом случае может возникнуть неполный гидроудар, при котором величина повышения давления (ударное давление) будет меньше, чем в первом случае, а формула Жуковского примет вид
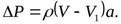
Приведённые формулы справедливы только в том случае, если время закрытия крана tЗАК меньше фазы гидравлического удара 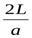 , т.е.
, т.е. 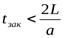 .
.
В том случае, если 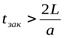 , возникает непрямойгидроудар. Для него характерно то, что отразившаяся от резервуара в начале трубы ударная волна возвращается к заслонке крана раньше, чем он будет полностью закрыт. Величина
, возникает непрямойгидроудар. Для него характерно то, что отразившаяся от резервуара в начале трубы ударная волна возвращается к заслонке крана раньше, чем он будет полностью закрыт. Величина 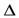 Р в этом случае будет меньше, чем при прямом гидроударе. Её приближенно (считая, что изменение Р в трубопроводе происходит по линейному закону) можно определить по формуле:
Р в этом случае будет меньше, чем при прямом гидроударе. Её приближенно (считая, что изменение Р в трубопроводе происходит по линейному закону) можно определить по формуле:
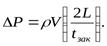
В  гидроприводах технологических машин, станков и т.п. очень часто возникает так называемыйгидроудар в тупиковом трубопроводе. В этом случае возможно увеличение ударного давления в два раза. Пояснить это можно следующим рисунком.
гидроприводах технологических машин, станков и т.п. очень часто возникает так называемыйгидроудар в тупиковом трубопроводе. В этом случае возможно увеличение ударного давления в два раза. Пояснить это можно следующим рисунком.
Т  рубопровод с низким начальным давлением отделён от источника гидравлической энергии высокого давления. При мгновенном (в реальных гидросистемах0,008 – 0,001с) открытии заслонки крана давление в начале трубопровода внезапно возрастает на величину
рубопровод с низким начальным давлением отделён от источника гидравлической энергии высокого давления. При мгновенном (в реальных гидросистемах0,008 – 0,001с) открытии заслонки крана давление в начале трубопровода внезапно возрастает на величину  Р =Р1 - РО.
Р =Р1 - РО.
В  озникает волна повышенного давления, которая движется к концу трубопровода со скоростьюа. Скорость же движения жидкости становится равной
озникает волна повышенного давления, которая движется к концу трубопровода со скоростьюа. Скорость же движения жидкости становится равной 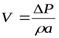 , а давление отличается отР0 на величину
, а давление отличается отР0 на величину 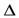 Р. В момент времени
Р. В момент времени 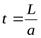 волна достигнет тупика, и вся труба окажется расширенной.
волна достигнет тупика, и вся труба окажется расширенной.
Т.к. дальнейшее движение жидкости невозможно, то передние её слои остановятся, а последующие по инерции будут набегать на них. Это вызовет дополнительное повышение давления в конце трубы на величину 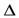 Р. Возникнет вторая, отражённая волна, которая движется к началу трубопровода со скоростью а.Давление за фронтом ударной волны становится Р2=Ро+2
Р. Возникнет вторая, отражённая волна, которая движется к началу трубопровода со скоростью а.Давление за фронтом ударной волны становится Р2=Ро+2 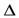 Р, а скорость жидкости V=0.
Р, а скорость жидкости V=0.
Далее весь процесс продолжается как в случае полного гидроудара, но колебания давления происходят относительно величины Р1=Ро+  Р, а не относительноРо.
Р, а не относительноРо.
Способы борьбы с ударным повышением давления.
Самый эффективный способ заключается в оборудовании сети регулирующими устройствами ( вентили и задвижки), которые не позволяют осуществлять быстрое и изменение скорости в трубах.
Воздушные колпаки или компенсаторы ограничивают распространение удара и ослабляют действие.
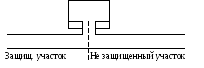
На незащищенном участке трубы ударное повышение давления действует только в течении 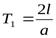
Вместо 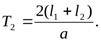 Таким образом импульс силы ослабевает (уменьшается) и трубы не рвутся.
Таким образом импульс силы ослабевает (уменьшается) и трубы не рвутся.
Лекция №10. Истечение жидкости из отверстий и насадков
Сжатие струи
Истечение через насадки
Истечение жидкости из отверстий и насадков (коротких трубок различной формы и сечений) характерно тем, что в этом процессе потенциальная энергия жидкости на очень коротком расстоянии и за очень короткое время превращается в кинетическую энергию струи (или капель в общем случае). При этом происходят какие-то, большие или не очень, потери напора. Подобные режимы течения жидкости возникают при вытекании жидкости из резервуаров, баков, котлов в атмосферу или пространство, заполненное жидкостью. Аналогичные явления происходят при протекании жидкости через малые отверстия и щели в направляющей, контрольной и регулирующей аппаратуре различных гидравлических систем.
Основной вопрос, на который нужно найти ответ, состоит в том, как определить расход и скорость истечения через отверстия или насадки различной формы.
Сжатие струи
П  ри вытекании жидкости из резервуара через отверстие в тонкой стенке, диаметр которого значительно меньше размеров резервуара, а края отверстия имеют прямоугольную форму, диаметр вытекающей струи будет меньше размеров диаметра отверстия. Это происходит потому, что жидкость, вытекающая из резервуара, попадает в отверстие со всех направлений, а после прохождения отверстия направление движения всех частиц жидкости становится одинаковым. Изменение направления движения частиц жидкости в силу их инерционности мгновенно произойти не может. Поэтому сжатие струи обусловлено необходимостью постепенного изменения направления движения жидкости при прохождении отверстия. Так как размеры резервуара много больше размеров отверстия, боковые поверхности и свободная поверхность не могут оказывать влияния на направление входа жидкости в отверстие, то в этом случае наблюдаетсясовершенное сжатие струи. Такое сжатие является наибольшим, и оно достигается на расстоянии примерно равном диаметру отверстия. Степень сжатия выражается коэффициентом сжатия
ри вытекании жидкости из резервуара через отверстие в тонкой стенке, диаметр которого значительно меньше размеров резервуара, а края отверстия имеют прямоугольную форму, диаметр вытекающей струи будет меньше размеров диаметра отверстия. Это происходит потому, что жидкость, вытекающая из резервуара, попадает в отверстие со всех направлений, а после прохождения отверстия направление движения всех частиц жидкости становится одинаковым. Изменение направления движения частиц жидкости в силу их инерционности мгновенно произойти не может. Поэтому сжатие струи обусловлено необходимостью постепенного изменения направления движения жидкости при прохождении отверстия. Так как размеры резервуара много больше размеров отверстия, боковые поверхности и свободная поверхность не могут оказывать влияния на направление входа жидкости в отверстие, то в этом случае наблюдаетсясовершенное сжатие струи. Такое сжатие является наибольшим, и оно достигается на расстоянии примерно равном диаметру отверстия. Степень сжатия выражается коэффициентом сжатия 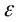 :
:

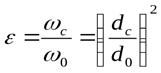 ,
,
 где
где 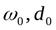 - площадь и диаметр отверстия,
- площадь и диаметр отверстия,

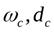 - площадь и диаметр совершенно сжатой струи.
- площадь и диаметр совершенно сжатой струи.
В том случае, если истечение происходит из резервуара такой формы, что его стенки влияют на траекторию движения частиц при входе в отверстие, наблюдается несовершенное сжатие струи.
В  следствие того, что боковые стенки резервуара перед отверстием формируют направление движения жидкости, струя после отверстия сжимается в меньшей степени, чем при вытекании из практически бесконечного резервуара. По этой причине меняется коэффициент сжатия струи. Формулы для определения этого сжатия для разных жидкостей и разных условий истечения - эмпирические. Например, для круглого центрального отверстия в тонкой торцовой стенке трубы и для маловязких жидкостей коэффициент сжатия
следствие того, что боковые стенки резервуара перед отверстием формируют направление движения жидкости, струя после отверстия сжимается в меньшей степени, чем при вытекании из практически бесконечного резервуара. По этой причине меняется коэффициент сжатия струи. Формулы для определения этого сжатия для разных жидкостей и разных условий истечения - эмпирические. Например, для круглого центрального отверстия в тонкой торцовой стенке трубы и для маловязких жидкостей коэффициент сжатия 
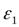 можно находить по следующей эмпирической формуле в долях от коэффициента сжатия
можно находить по следующей эмпирической формуле в долях от коэффициента сжатия 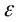 при совершенном сжатии струи
при совершенном сжатии струи
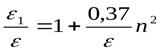 ;
;
где 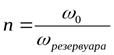 ;
;
где, в свою очередь, 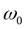 - площадь отверстия,
- площадь отверстия,
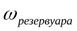 - площадь сечения резервуара (в приведённом примере площадь поперечного сечения трубы).
- площадь сечения резервуара (в приведённом примере площадь поперечного сечения трубы).
Истечение через малое отверстие в тонкой стенке
Рассмотрим большой резервуар с жидкостью, из которого через малое отверстие в боковой стенке вытекает струйка. Термины «большой резервуар» и «малое отверстие» означает, что эти размеры не сказываются на изменении высоты жидкости (напора) в резервуаре при вытекании из него жидкости. Термин «тонкая стенка» означает, что после сжатия струя вытекающей жидкости не касается цилиндрической поверхности отверстия.
Рассмотрим два сечения в этом резервуаре, обозначенные индексами 0 и С. Запишем уравнение Бернулли для этих условий:
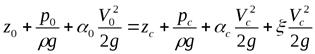 .
.
Д  ля описанных условий можно считать, что движения жидкости в сечении0 нет, следовательно, скоростной напор равен нулю. Разницей нивелирных высот, из-за их малого влияния можно пренебречь. Коэффициентом
ля описанных условий можно считать, что движения жидкости в сечении0 нет, следовательно, скоростной напор равен нулю. Разницей нивелирных высот, из-за их малого влияния можно пренебречь. Коэффициентом 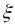 в данном случае обозначено сопротивление отверстия. Этот коэффициент учитывает потери энергии жидкости на сжатие струи и трение в струйках жидкости вблизи отверстии при формировании вытекающей струи. С учетом этого уравнение примет вид:
в данном случае обозначено сопротивление отверстия. Этот коэффициент учитывает потери энергии жидкости на сжатие струи и трение в струйках жидкости вблизи отверстии при формировании вытекающей струи. С учетом этого уравнение примет вид:

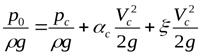 .
.
После перегруппировки членов получим
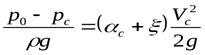 .
.
Выразим отсюда скорость
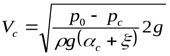 .
.
Заменим скорость отношением расхода к площади живого сечения потока и вновь перегруппируем
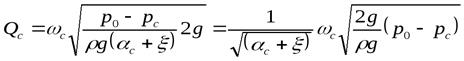 .
.
Проанализируем полученное выражение. Заметим, что индекс « с » относится к струе, и это единственный индекс, относящийся к движущейся жидкости «на выходе» рассматриваемого проходного сечения (определение приведено ниже). Опустим этот индекс. Величина 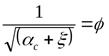 - называетсякоэффициентом скорости. Если считать распределение скоростей в струе равномерным (
- называетсякоэффициентом скорости. Если считать распределение скоростей в струе равномерным ( 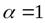 ), а жидкость идеальной, в которой нет потерь на трение, то коэффициент
), а жидкость идеальной, в которой нет потерь на трение, то коэффициент 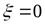 . Тогда коэффициент скорости
. Тогда коэффициент скорости 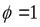 .
.
Отсюда становится понятным физический смысл коэффициента скорости. Он выражает отношениедействительного расхода через проходное сечение к теоретическому расходу.Действительным расходом называют расход, который на самом деле проходит через проходное сечение. Теоретический расход это такой, который мог бы протекать через проходное сечение при отсутствии потерь. Учтём, что 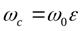 , где
, где 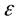 - коэффициент сжатия струи. После подстановки этих обозначений в коэффициент перед знаком радикала получим
- коэффициент сжатия струи. После подстановки этих обозначений в коэффициент перед знаком радикала получим 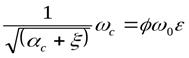 . Произведение
. Произведение 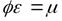 носит названиекоэффициент расхода. Тогда окончательно будем иметь формулу
носит названиекоэффициент расхода. Тогда окончательно будем иметь формулу
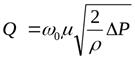 ,
,
или в другой форме, с учётом того, что 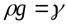
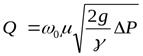 .
.
В этих формулах 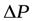 - разность давлений до проходного сечения и после него.
- разность давлений до проходного сечения и после него.
С помощью полученного выражения решается задача определения расхода для всех случаев течения жидкости под действием разности давлений. Кроме того, из данного выражения видно, что причиной течения жидкости является разность давлений. Жидкость всегда движется из области высокого давления область низкого давления. По существу приведённое выражение можно считатьинженерной формой уравнения Бернулли.
При прохождении жидкости через малое отверстие происходит «смятие» струи. На немецком языке «мятие» - «drosseln». Поэтому в технике истечение через малое отверстие называют дросселированием. Гидравлический аппарат, предназначенный для дросселирования, называется дросселем, а отверстие в этом гидроаппарате называется проходным сечением.
Наиболее сложной задачей практического применения этого уравнения является определение коэффициента 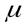 , значение которого зависит от степени сжатия струи и режима её течения, структуры распределения скоростей вблизи проходного сечения, которая в свою очередь зависит от формы входа в проходное сечение. Этот коэффициент определён экспериментально. Он, как и коэффициентыφ и ε, зависит от числа Рейнольдса и эти зависимости можно представить с помощью графика.
, значение которого зависит от степени сжатия струи и режима её течения, структуры распределения скоростей вблизи проходного сечения, которая в свою очередь зависит от формы входа в проходное сечение. Этот коэффициент определён экспериментально. Он, как и коэффициентыφ и ε, зависит от числа Рейнольдса и эти зависимости можно представить с помощью графика.
На графике буквамиReт обозначено число Рейнольдса, посчитанное по теоретической скорости, соответствующей теоретическому расходу.
С увеличением скорости истечения и связанным с этим увеличением Reт коэффициент скорости φ быстро нарастает и при Reт→ ∞стремится к значению φ =1,0. Это свидетельствует о значительном уменьшении гидравлического сопротивления отверстия за счёт снижения влияния вязкости.
Коэффициент сжатия струи ε с увеличением Reт уменьшается и при Reт→ ∞ стремится к значениюε = 0,6.
Коэффициент расхода μ, являясь произведением коэффициентов φ и ε, на первом этапе растёт, достигая максимального значения μ = 0,69 при Reт ≈ 350, а затем плавно снижается до μ ≈0,6.
Таким образом, только за счёт коэффициента μ величина расхода уменьшается на 30 – 40 %относительно теоретически возможного.
Истечение через насадки
Н  асадком называется короткая трубка длиной от двух до шести диаметров, присоединённая к выходу отверстия, через которое истекает жидкость. Роль насадка может выполнять и отверстие в толстой стенке, когда диаметр отверстия зна
асадком называется короткая трубка длиной от двух до шести диаметров, присоединённая к выходу отверстия, через которое истекает жидкость. Роль насадка может выполнять и отверстие в толстой стенке, когда диаметр отверстия зна
