Глава 3. Влияние диполь-дипольного взаимодействия на динамику двухкубитного перепутанного состояния
Основная проблема, которая возникает при физической реализации протоколов в физике квантовых вычислений является декогеренция, возникающая за счет взаимодействия с окружением. Однако, даже при отсутствии взаимодействия кубитов с окружением, степень перепутывания кубитов может меняться с течением времени, при этом возможны эффекты мгновенной смерти и рождения, перепутывания на временах меньших времени декогеренции, в частности для кубитов, взаимодействующих с квантовыми электромагнитными полями, в идеальных резонаторах изменение степени перепутывания кубитов вызвано осцилляциями Раби. Поэтому важной проблемой современной квантовой информатики является разработка эффективных механизмов, обеспечивающих стабилизацию перепутывания кубитов. Как уже отмечалось в главе 2, сверхпроводящие кубиты являются в настоящее время наиболее перспективными физическими системами для реализации протоколов квантовой информатики. Одной из важных отличительных черт сверхпроводящих кубитов, отличающих их от естественных атомов, являются большие значения эффективного дипольного момента, это позволяет реализовать для сверхпроводящих кубитов эффективное диполь-дипольное взаимодействие, которое может быть использовано для генерации и стабилизации перепутывания сверхпроводящих кубитов. Чтобы управлять и контролировать состояния перепутывания кубитов используется их взаимодействие с квантовыми полями копланарных резонаторов. В настоящее время имеется большое число работ, в которых как теоретически, так и экспериментально исследована динамика перепутывания кубитов взаимодействующих с копланарныи резонаторами. Однако преимущественно рассматривалось взаимодействие кубитов с общим полем единственного резонатора. Представляет интерес изучить динамику перепутывания кубитов взаимодействующих с различными резонаторами, при этом взаимодействие кубитов может быть реализовано за счет эффективного диполь дипольного взаимодействия.
Для этих целей рассмотрим два сверхпроводящих кубита, каждый из которых резонансно взаимодействует с изолированной модой микроволнового поля копланарного резонатора в вакуумном состоянии.
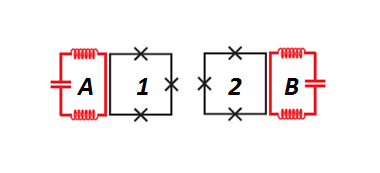
Рис.9 Схематическое изображение двух сверхпроводящих кубита, каждый из которых резонансно взаимодействует с изолированной модой микроволнового поля копланарного резонатора в вакуумном состоянии.
Взаимодействие между кубитами осуществляется за счет эфективно диполь-дипольного взаимодействия. Гамильтаниан данной системы можно записать в виде:
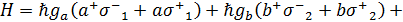
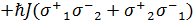 . (5.1)
. (5.1)
Где первые два слагаемых представляют эффективный гамильтониан невырожденного двухфотонного взаимодействия двухуровневых кубитов с полями резонаторов, 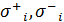 -повышающий и понижающий операторы в i-том двухуровневом кубите (i=1,2),
-повышающий и понижающий операторы в i-том двухуровневом кубите (i=1,2), 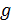 − эффективная константа двухфотонного взаимодействия кубита и резонатрного поля, третье слагаемое описывает эффективное диполь-дипольное взаимодействие кубитов,
− эффективная константа двухфотонного взаимодействия кубита и резонатрного поля, третье слагаемое описывает эффективное диполь-дипольное взаимодействие кубитов, 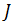 − параметр этого взаимодействия.
− параметр этого взаимодействия.
В дальнейшем для простоты будем рассматривать идентичные атомы и идентичные резонаторы, то есть 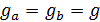 .
.
Выберем начальные состояние системы в виде:
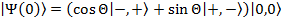 (5.2)
(5.2)
где 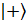 -возбужденное состояние i-го атома,
-возбужденное состояние i-го атома, 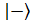 -основное состояние i-го атома,
-основное состояние i-го атома, 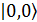 -вакуумное состояние двух резонаторов. Такое состояние может быть реализовано за счет взаимодействия кубитов общим полем третьего копланарного резонатора.
-вакуумное состояние двух резонаторов. Такое состояние может быть реализовано за счет взаимодействия кубитов общим полем третьего копланарного резонатора.
Временную функцию системы найдем из уравнения Шредингера:
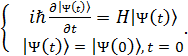 (5.3)
(5.3)
Будем искать решение уравнения в виде:
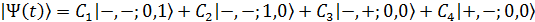 ,(5.4)
,(5.4)
где коэффициенты будут удовлетворять следующим уравнениям:
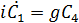 ,
,
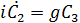 ,
,
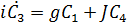 ,
,
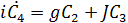 .
.
Найдем коэффициенты. После вычислений, получим следующие результаты:
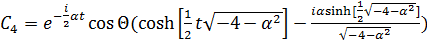 ,
,
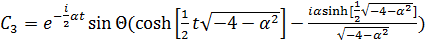 ,
,
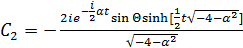 ,
,
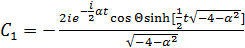 .
.
Для определения меры перепутывания воспользуемся параметром Переса-Хородецких:
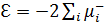 , (5.5)
, (5.5)
где 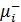 -отрицательные собственные значения транспонированной по
-отрицательные собственные значения транспонированной по
переменным одного кубита атомной матрицы плотности 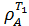 . Для неперепутанных состояний
. Для неперепутанных состояний 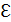 = 0. Для перепутанных состояний:
= 0. Для перепутанных состояний: 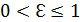 Максимальной степени перепутывания соответствует значение
Максимальной степени перепутывания соответствует значение 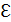 = 1.
= 1.
Запишем атомную матрицу плотности, соответствующему (5.3).
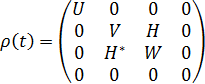 , (5.6)
, (5.6)
где 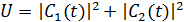 ,
, 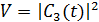 ,
, 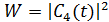 ,
, 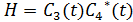 .
.
Частично транспонируя по переменным одного кубита, получим
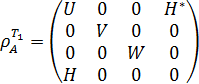 , (5.7)
, (5.7)
Тогда параметр Переса-Хородецких будет иметь вид:
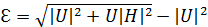 . (5.8)
. (5.8)
В таблице 1 показаны параметры экспериментов для сверхпроводящих кубитов, взаимодействующих с копланарными резонаторами. Из таблицы хорошо видно, что константа атом-полевого взаимодействия в таких экспериментах составляет несколько ГГц. Вместе с тем, в последнее время удалось реализовать эффективное взаимодействие кубитов g>3 ГГц. Это означает что в современных экспериментах достижимое значение параметра 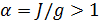 .
.
Таблица 1.Взаимодействие кубитов с копланарным микроволновым резонатором.
| Автор, год |  , (ГГц) , (ГГц) | 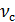 , (ГГц) , (ГГц) | T, (мК) | 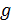 , (ГГц) , (ГГц) |
| M. Hofheinz, | 6-9 | 6.57 | 2,26 | |
| M. A Sillanpa, | 8,74 | 5,40 |
Результаты численного моделирования параметра перепутывания для начальных состояний двухатомной системы вида (5.2) и различных значений интенсивности диполь-дипольного взаимодействия представлены на рисунках 10 ,11 и 12. Из рисунков хорошо видно, что для начального состояния (5.2) диполь-дипольное взаимодействие во всех случаях приводит к значительной стабилизация степени перепутывания кубитов.
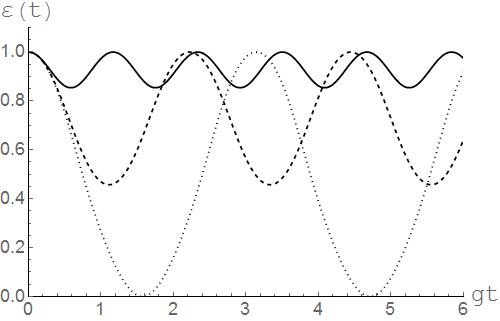
Рисунок 10. Временная зависимость параметра перепутывания 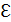 (t) для двухатомной системы с начальным состоянием (5.2) и значением параметра
(t) для двухатомной системы с начальным состоянием (5.2) и значением параметра 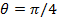 , параметр прямого диполь- дипольного взаимодействия J=0 (точки), J=2(тире), J=5 (сплошная линия).
, параметр прямого диполь- дипольного взаимодействия J=0 (точки), J=2(тире), J=5 (сплошная линия).
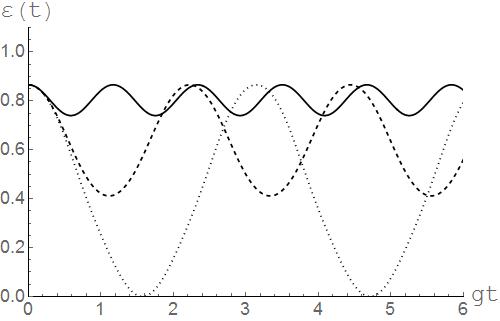
Рисунок 11. Временная зависимость параметра перепутывания 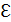 (t) для двухатомной системы с начальным состоянием (5.2) и значением параметра
(t) для двухатомной системы с начальным состоянием (5.2) и значением параметра 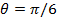 , параметр прямого диполь- дипольного взаимодействия J=0 (точки), J=2(тире), J=5 (сплошная линия).
, параметр прямого диполь- дипольного взаимодействия J=0 (точки), J=2(тире), J=5 (сплошная линия).
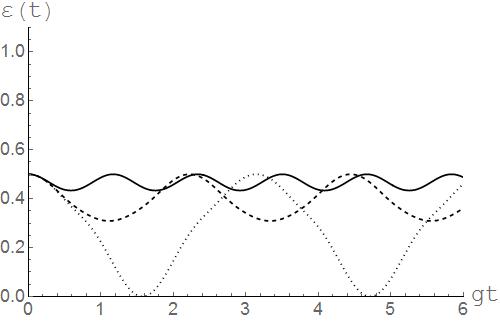
Рисунок 12. Временная зависимость параметра перепутывания 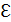 (t) для двухатомной системы с начальным состоянием (5.2) и значением параметра
(t) для двухатомной системы с начальным состоянием (5.2) и значением параметра 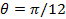 , параметр прямого диполь- дипольного взаимодействия J=0 (точки), J=2(тире), J=5 (сплошная линия).
, параметр прямого диполь- дипольного взаимодействия J=0 (точки), J=2(тире), J=5 (сплошная линия).
Таким образом компьютерное моделирование показало, что наведенное изначально перепутывание кубитов рассматриваемой модели может быть существенно стабилизировано, при наличии между сверхпроводящими кубитами интенсивного диполь-дипольного взаимодействия.
Заключение
В выпускной квалификационной работе было рассмотрено влияние диполь-дипольного взаимодействия на динамику двухкубитного перепутанного состояния.
При выполнении работы были достигнуты следующие результаты:
1. Найдены точные выражения для операторов эволюции для модели двух сверхпроводящих кубитов, каждый из которых резонансно взаимодействует с изолированной модой микроволнового поля копланарного резонатора в вакуумном состоянии.
2. Найдено точное решение уравнения Шредингера для временной функции.
3. Вычислен критерий перепутывания Переса-Хородецких.
4. Показано что наведенное изначально перепутывание кубитов рассматриваемой модели может быть существенно стабилизировано, при наличии между сверхпроводящими кубитами интенсивного диполь-дипольного взаимодействия.
Библиографический список
[1] Башаров, А.М. Квантовые Корреляции в системе двух двухуровневых атомов/ А.М. Башаров, А.А. Башкеев// Оптика и Спектроскопия. - 2004. - Т. 96. №5, С.716-723.
[2] Bashkirov, E.K. Entanglement induced by the two-mode thermal noise / E.K. Bashkirov// Laser Physics Letters. - 2006. – V.3, №3. – P.145-150.
[3] Башкиров, Е.К. Перепутывание двух дипольно связанных атомов/ Е.К. Башкиров, М.П. Ступацкая// Физика волновых процессов и радиотехнические системы - 2009. – Т.12, №2. – C.85-90.
[4] Башкиров, Е.К. Влияние штарковского сдвига на перепутывание двух атомов с вырожденными двухфотонными переходами/ Е.К. Башкиров, Ю.А. Никифорова// Вестник СамГУ. Естественнонаучная серия. - 2012. - №6(97) - С.174-178
[5] Башкиров, Е.К. Влияние диполь-дипольного взаимодействия на перепутывание в многофотонной модели Тависа-Каммингса / Е.К. Башкиров, М.С. Мастюгин // Вестник Самарского государственного университета. - 2011. № 8 (89). - С.153-156.
[6] Башкиров, Е.К. Перепутывание двух дипольно-связанных атомов, взаимодействующих с двухмодовым тепловым полем в резонаторе с высокой температурой / Е.К. Башкиров, М.С. Мастюгин // Вестник Самарского государственного университета. - 2012. - № 9 (100). - С. 151-158
[7] Башкиров, Е.К. Перепутывание в невырожденной двухфотонной модели Тависа-Каммингса / Е.К. Башкиров, М.С. Мастюгин // Вестник Самарского Государственного университета. - 2011. - № 5 (86). - С.109-114.61.
[8] Башкиров, Е.К. Влияние диполь-дипольного взаимодействия на динамику перепутанных сверхпроводящих потоковых кубитов, взаимодействующих с тепловым полем / Е.К. Башкиров, М.С. Мастюгин // Физика волновых процессов и радиотехнические системы. - 2013. - Т.16, № 2. -С.19-24.
[9] Башкиров, Е.К. Динамика перепутанных атомов с двухфотонными переходами при наличии штарковского сдвига энергетических уровней / Е.К. Башкиров, М.С. Мастюгин // Физика волновых процессов и радиотехнические системы. - 2014. - Т. 17, № 1. - С. 7-12. 133 64
[10] Скалли, М.О. Квантовая оптика/ М.О. Скалли, М.С. Зубайри: пер. с анг. под ред. В.В. Самарцева - Москва: ФИЗМАТЛИТ, 2003. - 512с.
[11] Алискендеров, А.И. Квантовые эффекты взаимодействия атома с излучением/ А.И. Алискендеров, A.C. Шумовский, Xo Чунг Зунг // Физика элементарных частиц и атомного ядра. - 1993. - Т. 24. Часть 2. - С. 409-463.
[12] Кондрашкин, М.П. Элементы квантовой информатики: учебное пособие / М.П. Кондрашкин, В.П. Яковлев - Москв, 2004. - 84с.
[13] Башкиров, Е.К. Перепутывание кубитов при наличии атомной когерентности/ Е.К. Башкиров, Д.В. Литвинова// Компьютерная оптика. − 2014. − Т.38, №4. – С. 663 – 669.
[14] DiCarlo L. et al. 2010 Preparation and measurement of three-qubit entanglement in a superconducting circuit Nature 467574
[15] Neeley M et al 2010 Generation of three-qubit entangled states using superconducting phase qubits Nature 467570.
[16] You J.Q, Nori F. Atom physics andquantum optics using superconducting cicuits // Nature. 2011. V. 474. P.589.
[17] Bylander J. et al. 2011 Noise spectroscopy through dynamical decoupling with a superconducting flux qubit Nature Phys. 7 565–70
[18] Hanson R, Kouwenhoven L P, Petta J R, Tarucha S and Vandersypen L M K 2007 Spins in few-electron quantum dots Rev. Mod. Phys. 791217
[19] Monz T. et al. 2011 14-qubit entanglement: creation and coherence Phys. Rev. Lett. 106130506
[20] Wilk T. et al. 2010 Entanglement of two individual neutral atoms using Rydberg blockade Phys.Rev. Lett. 104010502
[21] Zhang X L. et al. 2010 Deterministic entanglement of two neutral atoms via Rydberg blockade Phys. Rev. A 82030306
[22] Schumacker D., Westmoreland M.D. Quantum Processes, Systems, and Information - New York: Cambridge University Press, 2010.
[23] / M.B Plenio, S.F. Huelda, A. Beige A., P.L Knight. Cavity-loss-induced generation of entangled atoms // Phys. Rev.,1999. – Vol. A59. – №. 3. – P. 2468 - 2475.
[24] S. Bose, I. Fruentes-Guridi., P.L. Knight, V. Vedral.Subsystem purity as an enforcer of entanglement / // Phys. Rev. Lett., 2001. – Vol. 87. – 050401.
[25] M.S. Kim, J. Lee, D. Ahn, P.L. Knight. Entanglement induced by a single-mode heat environment / // Phys. Rev., 2002. – Vol. A65. – 040101.
[26] Zhou, L. Entanglement induced by a single-mode thermal field and criteria for entanglement / L. Zhou, H.S. Song // J. Opt., 2002. – Vol. B4. – P. 425 - 429.
[27] Peres A. // Phys. Rev. Lett. 1996. V. 77. P. 1413-1415.
[28] Horodecki R., Horodecki. M., Horodecki P. // Phys. Lett. 1996. V. A223. P. 333-339.
[29] Башкиров Е.К., Гришина Е. В., Сочкова Е. Ю. Атом-полевое перепутывание для модели Джейнса–Каммингса с зависящей от интенсивности константой взаимодействия // Вестн. Сам. гос. техн. ун-та. Сер.: Физ.-мат. науки. 2013. №2 (31) С.169-176.
[30] Наука и предельная реальность: квантовая теория, космология и сложность. Барроу Дж., Дэвис П., Харпер Ч. мл. (ред.-сост.); Мацарские В. и О. (пер. с англ.); Окунь Л.Б. (общ. науч. ред.). - М. Ин-т компьютер. исслед.; Ижевск: R&C Dynamics, 2013. - XVIII, 642 c.: ил. - Пер. изд.: Science and ultimate reality. Cambridge: Cambridge univ. press, cop. 2004. На обл. перед загл.: Барроу Дж., Дэвис П., Харпер Ч. мл. Библиогр. в конце ст. Предм. указ.: с. 611-642.
[31] Калашников Д. А. Пространственно-неоднородные источники бифотонных полей с контролируемыми спектральными и поляризационными свойствами: - Казань, 2009. - 134 с.
[32] Perfectly and imperfectly controlled quantum operations on a charge qubit Tsukanov A.V., Valiev K.A. Russian Microelectronics. 2007. Т. 36. № 2. С. 67-80.
[33] Балашов В.В., В.К.Долинов - Курс квантовой механики. Ижевск, РХД, 2001. - 336 стр.
[34] Барабанов, А. Л. Симметрии и спин-угловые корреляции в реакциях и распадах: Москва, 2008. – 662 с.
[35] Федоров М.В, П. А. Волков, Ю. М. Михайлова. Кутриты и кукварты в спонтанном параметрическом рассеянии света, корреляции и перепутывание состояний // Журнал экспериментальной и теоретической физики. - 2012. - Т. 142, вып. 1. - С. 20-43.
[36] Чернявский, А. Ю. Минимум энтропии измерений как вычислимая мера запутанности многочастичных квантовых состояний. Москва,2010. – 130 с.
[37] Омельянчук А. Н., Ильичев Е.В., Шевченко С.Н. Квантовые когерентные явления в джозефсоновских кубитах. – Киев. – 2013. – 184 с.
[38] Я. С. Гринберг, Ильичев, Е. В. Квантовая информатика и квантовые биты на основе сверхпроводниковых джозефсоновских структур: учеб. / Я. С. Гринберг, Е. В. Ильичев. — Новосибирск: Изд-во НГТУ, 2013. — ISBN 978-5-7782-2287-8
[39] Старобогатов Р.О. Сверхпроводящие модели кубитов // Вестник ИНЖЭКОНа, 2009. т.Вып. 8 (35). -с.27-32
[40] Кайе Ф., Лафламм Р., Моска М. Введение в квантовые вычисления //Учеб. пособие/Ф. Кайе, Р. Лафламм Ижевск: РХД. – 2009.
[41] Башкиров, Е.К. Перепутывание двух сверхпроводящих кубитов, взаимодействующих с двухмодовым тепловым полем / Е.К. Башкиров, М.С.Мастюгин // Компьютерная оптика. - 2013. - Т.37, № 3. - С. 278-285.
[42] Башкиров Евгений Константинович, Литвинова Дарья Вадимовна Перепутывание кубитов при наличии атомной когерентности // КО. 2014. №4 С.663-669.
Приложение
Программа, для выполнения математического моделирования:


