Квантование состояний электрона в канале полевого транзистора

КВАНТОВАНИЕ СОСТОЯНИЙ ЭЛЕКТРОНА В КАНАЛЕ ПОЛЕВОГО ТРАНЗИСТОРА

Выпускная квалификационная работа

Выполнил студент 4 курса

Орищенко Никита Сергеевич

____________

Научный руководитель

к.ф. – м.н., доцент

Цирова И.С.

____________

Допустить к защите

Зав. кафедрой общей

теоретической физики

д. ф. – м. н., профессор

Бирюков А.А.

___________

«__» _______ 2017 г.

Самара 2017

Оглавление

Введение. 3

Глава 1. Модель Джейнса-Каммингса. Кубит. 7

1.1. Модель Джейнса-Каммингса. 7

1.2. Кубит. 10

1.2.1. Матрица плотности чистого состояния. 11

1.2.2. Матрица плотности смешанного состояния. 12

1.2.3. Матрица плотности кубита. 12

Глава 2. Сверхпроводящие кубиты.. 14

2.1. Свойства сверхпроводников. 14

2.2. Эффект Брайана Джозефсона. 17

2.3. Сверхпроводящие кубиты.. 19

Глава 3. Влияние диполь-дипольного взаимодействия на динамику двухкубитного перепутанного состояния. 22

Заключение. 28

Библиографический список. 29

Приложение. 34

Введение

В начале 2000-х годов была выдвинута гипотеза о возможности использования так называемых "искусственных" атомов (сверхпроводящие джозефсоновские кольца, квантовые точки, примесные спины и т.д.), для создания новых уникальных квантовых приборов, таких как квантовый компьютер, квантовая сеть, одноэлектронный транзистор и т.д. Наиболее востребованными для практического применения "искусственными" атомами являются сверхпроводящие джозефсоновские кубиты.

Следующим шагом стали эксперименты, описанные в статьях [3]-[11], с различными видами искусственных атомов, которые активно проводятся последние 10 лет. В России сотрудники Московского физико-технического института, Российского квантового центра, Национального исследовательского технологического университета МИСиС, Института физики твердого тела РАН и ряда других организаций под руководством Олега Астафьева, Алексея Устинова и Валерия Рязанова смогли впервые получить сверхпроводящий кубит в 2015 году. В настоящее время в различных странах реализуются долгосрочные программы [12]-[18] по использованию искусственных атомов для создания различных квантовых приборов для квантовых вычислений, квантовых телекоммуникаций и т.д. В частности, в работе [18] представлена программа работ по реализации протоколов квантовой криптографии между космическим спутником и наземной станции.

Однако, для работы квантовых приборов, базирующихся на использовании "искусственных" атомов (нейтральных атомов, ионов, сверхпроводящих кубитов, квантовых точек и т.д.) необходимо использовать перепутанные состояния таких объектов. В настоящее время проведено большое количество экспериментов [3]-[11], в которых были реализованы перепутанные состояния для различных искусственных атомов, а также разработаны эффективные схемы управления и контроля степени их перепутанности.

Перепутанные состояния [15] это основная составляющая квантовой информатики, они будут широко использованы для квантовой телепортации и коммуникаций, для решения вычислительных задач, связанных с многочастичными системами и т.д. Для управления перепутанных естественных и искусственных атомов используют их взаимодействие с классическими, квантовыми электромагнитным полями и другими бозонными полями [16]-[24].

Для теоретического описания таких систем используется Модель Джейнса-Каммингса и ее обобщения [4], [9]-[13]. Но для создания квантовых приборов наиболее интересными являются многокубитные системы. В таком случае при теоретическом описании удобнее пользоваться моделью Тависа-Каммингса. С ее помощью можно более полно описать особенности перепутывания, в следствие взаимодействия различных полей с атомами. Модели многокубитных систем [8] на сегодняшний день, вызывают наибольший интерес из-за возможности аналитически описать квантовые эффекты взаимодействия излучения и вещества [28], а также их практическую реализацию. Изучение перепутанных состояний в многокубитных системах является приоритетной задачей квантовой информатики и лазерной физики в связи с практическими потребностями физики квантовых вычислений, создания квантовых сетей и др.

При взаимодействии окружающей среды и системы перепутанных кубитов происходит декогеренция и распад перепутанных состояний. Перепутывание также может исчезать и возрождаться на временах, меньших, чем время релаксации системы [28]. Такой эффект называется «мгновенной смертью» перепутывания. Исходя из этого важнейшей задачей при описании динамики кубитов является предотвращение, минимизация и использование влияния шума. Было выдвинуто много решений данной задачи, но многие из них требовали подключения дополнительных источников, либо были эффективны только при особых условиях.

С другой стороны, в целом ряде работ [22]-[25] была высказана гипотеза о том, что, напротив, шум и диссипация являются источниками перепутывания. Так же было рассмотрены различное схемы влияния разных видов шума и процессов диссипации на исчезновение и возникновение перепутанных состояний. Возможность генерации перепутывания кубитов в следствие взаимодействия теплового поля и системы была описана в целом ряде работ. В работе Питера Найта [23] была впервые описана возможность перепутывания двух идентичных кубитов взаимодействующих с общей модой теплового поля идеального резонатора. В последствие указанная модель была обобщена на случай неидентичных атомов, двухфотонных взаимодействий, наличия диполь-дипольного взаимодействия и др. Представляют интерес рассмотреть возможность перепутывания двух идентичных дипольно-связанных кубитов, каждая из которых взаимодействует с модой теплового электромагнитного поля в отдельном резонаторе. В квантовой оптике такая модель часто называется двойной двухатомной моделью Джейнса-Каммингса [29]. Такая модель наиболее просто может быть реализована для системы двух сверхпроводящих кубитов, каждый их которых взаимодействует со своим копланарным микроволновым резонатором или сверхпроводящим LC контуром.

Целью работы является изучение особенностей динамики перепутывания двух дипольно-связанных сверхпроводящих потоковых кубитов, каждый из которых взаимодействует с изолированной модой микроволнового поля копланарного резонатора в вакуумном состоянии.

Для достижения данных целей в ходе работы были поставлены следующие задачи:

- Найти точное решение модели.

- Вычислить параметр перепутывания кубитов – отрицательность.

-Исследовать путем численного моделирования зависимость отрицательности от параметров модели и начального состояния атомов.

Структура и объем работы

Работа изложена на 34 страницах печатного текста. Состоит из введения, 3 глав, заключения и библиографический список, который включает 41 наименования. Общий объем работы 34 траниц текста.

Модель Джейнса-Каммингса

Модель Джейнса- Каммнгса была предложена в 1963 году Эдвином Джейнсом и Фредом Каммингсом при сравнении полуклассической теории спонтанного излучения и квантовой теории излучения. В полуклассической теории взаимодействия атом-поле, поле рассматривалось как функция времени, а не как оператор, атом же квантовался. Многие явления в современной оптике описываются полуклассической теорией (например, цикл Раби).

Модель Джейнса-Каммингса показала, что на эволюцию состояния двухуровневой системы влияет квантование поля излучения по сравнению с полуклассической теорией взаимодействия света и атомов. Так же было обнаружено, дискретность состояния поля влечет за собой распад и возрождение атомной инверсии. Такой чисто квантовый эффект может быть описан моделью Джейнса-Каммингса, но только в случае полуклассической теории. В 1987 году Ремпе, Вальтер, и Кляйн продемонстрировали случай квантовых коллапсов (распадов) и ревайвэлов (возрождений) в одноатомном мазере.

Рассмотрим модель Джейнса-Каммингса подробнее. Для данной системы можно записать гамильтониан с помощью гамильтониана из классической электродинамики. Нерелятивистский электрон взаимодействует с потенциальным полем U(r) и электромагнитным полем с потенциалом A(r). Классический гамильтониан для такой системы будет иметь вид:

, (1.1)

Каждое слагаемое распишем:

.

здесь p-импульс электрона, m-его масса, e-заряд. ,

,электромагнитное поле поперечное. Член описывает возмущение, а гамильтониан невозмущенной системы, в рамках теории возмущения.

Само представление о двухуровневом атоме построено на предположении о том, что из всех возможных состояний мы можем ограничится лишь двумя, и ограничение накладывается так же моду поля, в данном случае рассматривается одна мода поля.

Состояние атома, как известно, ограничивается правилами отбора и характеризуется значениями момента и четности. В модели Джейнса-Каммингса всевозможные типы переходов, в частности дипольные переходы.

Задача сводится к вычислению члена в выбранном базисе, но обычно этим членом пренебрегают, а более точное вычисление приводит к перенормировке массы.

Запишем векторный потенциал в рамках вторичного квантования для одной моды поля:

, (1.2)

где e-единичный вектор поляризации, - частота, -объем квантования.

Так как объемы атома намного меньше чем длина волны оптического излучения, то мы можем прибегнуть к следующему приближению: . Тогда для матричных элементов в данном приближении:

Беря в учет соотношение , заменим матричные элементы импульса на радиус-вектор. Так же введем атомные операторы

Тогда гамильтониан будет иметь вид:

, (1.3)

где , , , , .

Дальше нужно из исключить члены , . В итоге мы приходим к модели Джейнса-Каммингса:

. (1.4)

Можно подчеркнуть, что аналогичный по структуре гамильтониан можно получить при приближении , подробнее этот вопрос можно рассмотреть в работе [16].

Кубит

Квантово-механические процессы, как правило, описываются переходами между энергетическими уровнями [37]. Один из уровней описывает начальное состояние до перехода, второй уровень-конечное состояние после перехода. Нужно отметить, что такой переход так же может осуществляться через несколько промежуточных состояний.

Существует система, называемая кубитом, в которой можно ограничится рассмотрением двух уровней.

Применим постулаты квантовой механики к описанию кубита. Пространство состояний кубита является двумерным гильбертовым пространством. Вектор произвольного состояния кубита есть когерентная линейная суперпозиция базисных состояний:

, (2.1)

где - комплексные числа, удовлетворяющие условию нормировки: ; векторы и – ортонормированные базисные состояния. При этом положении кубит находится в обоих состояниях одновременно. Базисные состояния кубита могут быть выбраны произвольным образом, различается лишь поворот в двухмерном базисном состоянии. Выбор базиса определяется измерительным процессом.

С помощью вектора состояния 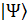описывается «чистое» состояние, состояние замкнутой квантовой системы. На самом деле данная система рассматривается в совокупности квантовой системы, которая взаимодействует с окружением (Рисунок 1).

Рис. 1. Смешанное состояние ,являющаяся частью системы.

Чтобы описать отельные подсистемы нужно пользоваться матрицей плотности 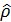. Опишем систему, состояние которой нам не полностью известно, для этого воспользуемся понятием статистического ансамбля чистых состояний, вероятность нахождения системы в них равна . Таким состоянием системы называют смешанное состояние.

Матрица плотности кубита

При учете, что: 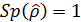, матрица плотности кубита будет иметь вид:

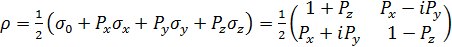. (2.8)

Вектор 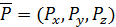показывает координаты точки внутри сферы Блоха, которые соответствуют состоянию кубита 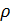. Все точки, представляющие смешанные состояния лежат внутри сферы Блоха. Например, 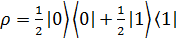полностью смешанное состояние, находится в точке центра сферы Блоха.

Свойства сверхпроводников

Одним из наиболее ярких открытий 20 века стала сверхпроводимость. Камерлинг Оннес в 1911 обнаружил данное свойство. Главным параметров сверхпроводников является критическая температура 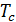, если показание температуры будет ниже данного показателя, то его сопротивление становится равным нулю. Показатель критической температуры очень низок, из-за этого многие физики поставили перед собой задачу о повышении показателя критической температуры.

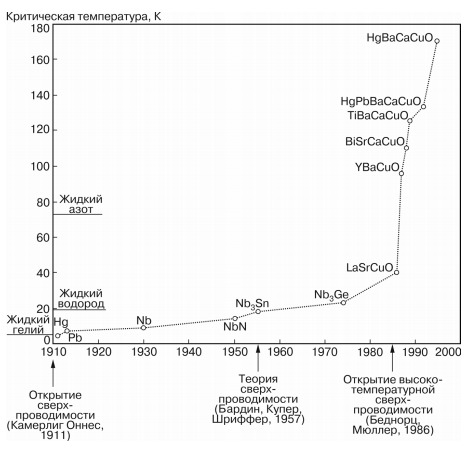
Рис. 3. Хронология повышения температуры сверхпроводящего провода.

В 1986 году произошел настоящий скачек Дж. Борнорец и К. Мюллер открыли сверхпроводимость при высоких температурах, которая превысила температуру кипения жидкого азота (-196 ⁰C).

Рассмотрим фундаментальные свойства сверхпроводников, установленные теоретически и подтверждённые на опыте.

Бесконечная проводимость

Проводимость сверхпроводника будет стремиться к бесконечности, так как сопротивление будет равно нулю. При температуре 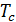и с понижением температуры происходит переход в сверхпроводящее состояние. Если рассмотреть ток, протекающий через сверхпроводник, то мы увидим, что он будет являться бездиссипативным. Тогда исходя из закона Джоуля-Ленца

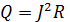, мы можем сделать вывод, что мощность будет равна нулю.

Идеальный дагмагнетизм

Бесконечная проводимость не могла объяснить особое поведение сверхпроводника в магнитном поле. Вальтер Мейсснер и Роберт Оксенфельд выяснили что магнитное поле не проходит сквозь толщу сверхпроводника. По всей области сверхпроводника, кроме области близкой к поверхности, магнитная индукция равна нулю.

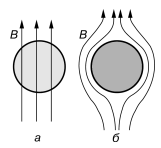
Рис. 4. Эффект Вальтера Мейсснера. Магнитное поле выталкивается из сверхпроводника. (а)-нормальный металл, (б)-сверхпроводник

Энергетическая щель

По сравнению с термодинамическими свойствами металлов, термодинамические свойства сверхпроводников так же отличаются. В спектре квазичастичных электронных возбуждений есть запрещенный интервал энергии, так же называемый щелью Δ. Значение температуры существенно влияет на величину щели.

Квантование магнитного потока

Рассмотрим массивное кольцо, состоящее из сверхпроводника. В таком кольце циркулирующий ток, а также создаваемое им магнитное поле не могут принимать произвольные значения. Другими словами, в отверстии поток магнитного поля Φ принимает лишь дискретные значения:

.

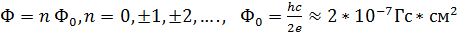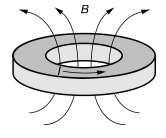
Рис. 5. Магнитное поле, создаваемое циркулирующим током в сверхпроводящем кольце.

Квазистатичные возбуждения

Вследствии уменьшения температуры сверхпроводника процессы диссипации и декогерентности существенно подавляются. Для обеспечения в сверхпроводниках низкого уровня процессов диссипации и декогерентности нужно чтобы выполнялись условия: 1) 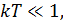2) .

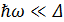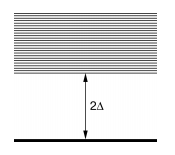
Рис. 6. Квазичастичные возбуждения в сверхпроводнике.

Эффект Брайана Джозефсона

Сверхпроводящие структуры, содержащие джозефсонские контакты, являются основой для джозефсоноских контактов. Такие контакты состоят из двух сверхпроводников, разделенных тонким слоем диэлектрика.

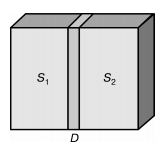
Рис.7 Джозефсонский контакт.

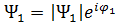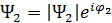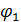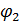Сверхпроводник S₁ характеризуется волновой функцией , а сверхпроводник S₂ характеризуется функцией . Если между берегами не будет взаимодействия, то это приведет к отсутствию корреляции меду фазами, но при этом фазы и когерентны в каждом из проводников. Обмен электронами приводит к фазовой когерентности в системе и установлению разности фаз 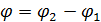на контакте. Открытие состоит в том, что сверхпроводящий ток может протекать без сопротивления через туннельный барьер диэлектрика, а значение будет связано с разностью фаз 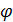[38].

Джозефсон определил два эффекта:

Стационарный Джозефсонский эффект

Первым соотношением Джозефсона определяется зависимость сверхпроводящего тока, проходящего через туннельный барьер, от разности фаз на контакте:

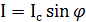. (3.1)

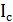- это критический ток, показывающее максимальное значение бездиссипативного тока, проходящего через контакт. При повышении критического тока появляется диссипативная компонента тока квазичастиц, тем самым вызывая возникновение напряжения .

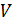Нестационарный Джозефсонский эффект

Связь напряжения на контакте с производной фазы по времени описывает второе соотношение Джозефсона:

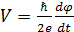. (3.2)

Если к джозефскому контакту приложить постоянный ток, что приложенный ток, согласно соотношениям Джозефсона, будет ассоциировать с частотой:

(3.3)

Постоянное напряжение на концах контактов двух сверхпроводников вызывает переменный ассоциирующий ток.

Эффект Джозефсона наблюдается даже при слабой связи между сверхпроводниками. Разные типы сверхпроводящих контактов (микро-мостики, точечные контакты) обладают различными ток-фазовыми зависимостями 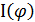, которые обладают 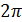- периодичностью, но неявляются синусоидальными.

Сверхпроводящие кубиты

Сверхпроводящие кубиты реализуются путем использования методов «теневого напыления» и электронно-лучевой литографии. Сверхпроводящие кубиты состоят из сверхпроводниковых петель, размеры которых сравнимы с микронными размерами, в эти петли вживляются джозефсоновские переходы. Джозефсоновские переходы обладают нелинейной индуктивностью и емкостью. Как было сказано в предыдущем разделе, где был описан эффект Джозефсона [38], при «разрыве» сверхпроводника слабой связью, по сверхпроводнику начинает течь ток 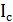, который зависит от разности фаз 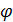сверхпроводящих электронов. Если сравнить эффективный гамильтониан системы, описывающей переход, с гамильтонианом нелинейного маятника, то можно заметить, что они схожи, притом угол отклонения маятника от состояния покоя играет роль разности фаз на берегах контакта. Но чтобы использовать систему с джозевсоновскими переходами в качестве логического элемента, нужно чтобы выполнялись определенные условия:

1. Эффект шумов.

Цепь должна полностью состоять из сверхпроводников, так же должны использоваться сверхнизкие температуры для так называемого «замораживания» квазичастотных возбуждений. То есть энергия тепловых флуктуаций должна быть много меньше чем расстояние между самыми нижними уровнями энергитического спектра 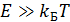,где 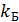- постоянная Больцмана. То есть температура должна придерживаться в районе нескольки мК.

2. Отделение двух уровней от основного энергетического спектра

Если создать нелинейную индуктивность контакта, то это условие будет выполняться.

Чтобы описать квантовые свойства джозефсоноских систем, нужно применить методику канонически сопряженных переменных. Получаем следующий коммутатор 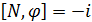. То есть параметры N- число куперовских пар и 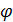- разность фаз не могут быть одновременно определены, они испытывают квантовые флуктуации. Если провести аналогию, то мы можем прийти к следующему выражению 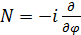. Тогда мы можем записать гамильтониан нелинейного осциллятора, в случае обособленного джозефсоновского контакта с током :

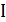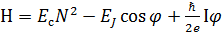, (4.1)

где 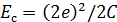-кулоновская энергия, необходимая для сдерживания куперовских пар при заряде 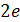и 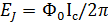-джозефсоновская энергия, приходящаяся на связь кванта потока 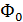в нелинейной индуктивности

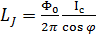, что является самой мерой силы связи джозефсоновского перехода. Можно сделать вывод что из-за квантового туннелирования через потенциальный барьер удержание частицы в потенциальной яме невозможно [38]. Однако, при условии, что полная энергия будет много меньше энергии джозефсона 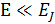вероятность такого туннелирования становится очень малой, так же частота перехода между уровнями кубита имеет большую зависимость от соотношения между кулоновской и джозефсоновской энергиями [38].

В зависимости от соотношения между кулоновской энергией и джозефсоновской энергией сверхпроводящие кубиты можно подразделить на три группы: зарядовый, потоковый и фазовый кубиты. Соотношения между энергиями можно менять разными способами, например, меняя размер джозефсоновского перехода, что вносит вклад и в емкость, тем самым меняя энергию. Каждый из трех реализованных типов имеет свои преимущества, а также и недостатки.

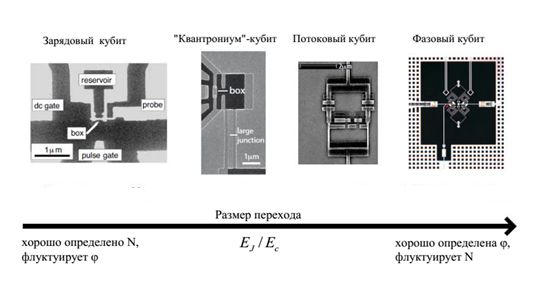
Рис.8 Изображения со сканирующего электронного микроскопа различных типов сверхпроводящих кубитов. Отношение 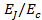возрастает с увеличением размеров перехода, что, в свою очередь, определяет, какая из двух канонически сопряженных величин, j или N

Заключение

В выпускной квалификационной работе было рассмотрено влияние диполь-дипольного взаимодействия на динамику двухкубитного перепутанного состояния.

При выполнении работы были достигнуты следующие результаты:

1. Найдены точные выражения для операторов эволюции для модели двух сверхпроводящих кубитов, каждый из которых резонансно взаимодействует с изолированной модой микроволнового поля копланарного резонатора в вакуумном состоянии.

2. Найдено точное решение уравнения Шредингера для временной функции.

3. Вычислен критерий перепутывания Переса-Хородецких.

4. Показано что наведенное изначально перепутывание кубитов рассматриваемой модели может быть существенно стабилизировано, при наличии между сверхпроводящими кубитами интенсивного диполь-дипольного взаимодействия.

Библиографический список

[1] Башаров, А.М. Квантовые Корреляции в системе двух двухуровневых атомов/ А.М. Башаров, А.А. Башкеев// Оптика и Спектроскопия. - 2004. - Т. 96. №5, С.716-723.

[2] Bashkirov, E.K. Entanglement induced by the two-mode thermal noise / E.K. Bashkirov// Laser Physics Letters. - 2006. – V.3, №3. – P.145-150.

[3] Башкиров, Е.К. Перепутывание двух дипольно связанных атомов/ Е.К. Башкиров, М.П. Ступацкая// Физика волновых процессов и радиотехнические системы - 2009. – Т.12, №2. – C.85-90.

[4] Башкиров, Е.К. Влияние штарковского сдвига на перепутывание двух атомов с вырожденными двухфотонными переходами/ Е.К. Башкиров, Ю.А. Никифорова// Вестник СамГУ. Естественнонаучная серия. - 2012. - №6(97) - С.174-178

[5] Башкиров, Е.К. Влияние диполь-дипольного взаимодействия на перепутывание в многофотонной модели Тависа-Каммингса / Е.К. Башкиров, М.С. Мастюгин // Вестник Самарского государственного университета. - 2011. № 8 (89). - С.153-156.

[6] Башкиров, Е.К. Перепутывание двух дипольно-связанных атомов, взаимодействующих с двухмодовым тепловым полем в резонаторе с высокой температурой / Е.К. Башкиров, М.С. Мастюгин // Вестник Самарского государственного университета. - 2012. - № 9 (100). - С. 151-158

[7] Башкиров, Е.К. Перепутывание в невырожденной двухфотонной модели Тависа-Каммингса / Е.К. Башкиров, М.С. Мастюгин // Вестник Самарского Государственного университета. - 2011. - № 5 (86). - С.109-114.61.

[8] Башкиров, Е.К. Влияние диполь-дипольного взаимодействия на динамику перепутанных сверхпроводящих потоковых кубитов, взаимодействующих с тепловым полем / Е.К. Башкиров, М.С. Мастюгин // Физика волновых процессов и радиотехнические системы. - 2013. - Т.16, № 2. -С.19-24.

[9] Башкиров, Е.К. Динамика перепутанных атомов с двухфотонными переходами при наличии штарковского сдвига энергетических уровней / Е.К. Башкиров, М.С. Мастюгин // Физика волновых процессов и радиотехнические системы. - 2014. - Т. 17, № 1. - С. 7-12. 133 64

[10] Скалли, М.О. Квантовая оптика/ М.О. Скалли, М.С. Зубайри: пер. с анг. под ред. В.В. Самарцева - Москва: ФИЗМАТЛИТ, 2003. - 512с.

[11] Алискендеров, А.И. Квантовые эффекты взаимодействия атома с излучением/ А.И. Алискендеров, A.C. Шумовский, Xo Чунг Зунг // Физика элементарных частиц и атомного ядра. - 1993. - Т. 24. Часть 2. - С. 409-463.

[12] Кондрашкин, М.П. Элементы квантовой информатики: учебное пособие / М.П. Кондрашкин, В.П. Яковлев - Москв, 2004. - 84с.

[13] Башкиров, Е.К. Перепутывание кубитов при наличии атомной когерентности/ Е.К. Башкиров, Д.В. Литвинова// Компьютерная оптика. − 2014. − Т.38, №4. – С. 663 – 669.

[14] DiCarlo L. et al. 2010 Preparation and measurement of three-qubit entanglement in a superconducting circuit Nature 467574

[15] Neeley M et al 2010 Generation of three-qubit entangled states using superconducting phase qubits Nature 467570.

[16] You J.Q, Nori F. Atom physics andquantum optics using superconducting cicuits // Nature. 2011. V. 474. P.589.

[17] Bylander J. et al. 2011 Noise spectroscopy through dynamical decoupling with a superconducting flux qubit Nature Phys. 7 565–70

[18] Hanson R, Kouwenhoven L P, Petta J R, Tarucha S and Vandersypen L M K 2007 Spins in few-electron quantum dots Rev. Mod. Phys. 791217

[19] Monz T. et al. 2011 14-qubit entanglement: creation and coherence Phys. Rev. Lett. 106130506

[20] Wilk T. et al. 2010 Entanglement of two individual neutral atoms using Rydberg blockade Phys.Rev. Lett. 104010502

[21] Zhang X L. et al. 2010 Deterministic entanglement of two neutral atoms via Rydberg blockade Phys. Rev. A 82030306

[22] Schumacker D., Westmoreland M.D. Quantum Processes, Systems, and Information - New York: Cambridge University Press, 2010.

[23] / M.B Plenio, S.F. Huelda, A. Beige A., P.L Knight. Cavity-loss-induced generation of entangled atoms // Phys. Rev.,1999. – Vol. A59. – №. 3. – P. 2468 - 2475.

[24] S. Bose, I. Fruentes-Guridi., P.L. Knight, V. Vedral.Subsystem purity as an enforcer of entanglement / // Phys. Rev. Lett., 2001. – Vol. 87. – 050401.

[25] M.S. Kim, J. Lee, D. Ahn, P.L. Knight. Entanglement induced by a single-mode heat environment / // Phys. Rev., 2002. – Vol. A65. – 040101.

[26] Zhou, L. Entanglement induced by a single-mode thermal field and criteria for entanglement / L. Zhou, H.S. Song // J. Opt., 2002. – Vol. B4. – P. 425 - 429.

[27] Peres A. // Phys. Rev. Lett. 1996. V. 77. P. 1413-1415.

[28] Horodecki R., Horodecki. M., Horodecki P. // Phys. Lett. 1996. V. A223. P. 333-339.

[29] Башкиров Е.К., Гришина Е. В., Сочкова Е. Ю. Атом-полевое перепутывание для модели Джейнса–Каммингса с зависящей от интенсивности константой взаимодействия // Вестн. Сам. гос. техн. ун-та. Сер.: Физ.-мат. науки. 2013. №2 (31) С.169-176.

[30] Наука и предельная реальность: квантовая теория, космология и сложность. Барроу Дж., Дэвис П., Харпер Ч. мл. (ред.-сост.); Мацарские В. и О. (пер. с англ.); Окунь Л.Б. (общ. науч. ред.). - М. Ин-т компьютер. исслед.; Ижевск: R&C Dynamics, 2013. - XVIII, 642 c.: ил. - Пер. изд.: Science and ultimate reality. Cambridge: Cambridge univ. press, cop. 2004. На обл. перед загл.: Барроу Дж., Дэвис П., Харпер Ч. мл. Библиогр. в конце ст. Предм. указ.: с. 611-642.

[31] Калашников Д. А. Пространственно-неоднородные источники бифотонных полей с контролируемыми спектральными и поляризационными свойствами: - Казань, 2009. - 134 с.

[32] Perfectly and imperfectly controlled quantum operations on a charge qubit Tsukanov A.V., Valiev K.A. Russian Microelectronics. 2007. Т. 36. № 2. С. 67-80.

[33] Балашов В.В., В.К.Долинов - Курс квантовой механики. Ижевск, РХД, 2001. - 336 стр.

[34] Барабанов, А. Л. Симметрии и спин-угловые корреляции в реакциях и распадах: Москва, 2008. – 662 с.

[35] Федоров М.В, П. А. Волков, Ю. М. Михайлова. Кутриты и кукварты в спонтанном параметрическом рассеянии света, корреляции и перепутывание состояний // Журнал экспериментальной и теоретической физики. - 2012. - Т. 142, вып. 1. - С. 20-43.

[36] Чернявский, А. Ю. Минимум энтропии измерений как вычислимая мера запутанности многочастичных квантовых состояний. Москва,2010. – 130 с.

[37] Омельянчук А. Н., Ильичев Е.В., Шевченко С.Н. Квантовые когерентные явления в джозефсоновских кубитах. – Киев. – 2013. – 184 с.

[38] Я. С. Гринберг, Ильичев, Е. В. Квантовая информатика и квантовые биты на основе сверхпроводниковых джозефсоновских структур: учеб. / Я. С. Гринберг, Е. В. Ильичев. — Новосибирск: Изд-во НГТУ, 2013. — ISBN 978-5-7782-2287-8

[39] Старобогатов Р.О. Сверхпроводящие модели кубитов // Вестник ИНЖЭКОНа, 2009. т.Вып. 8 (35). -с.27-32

[40] Кайе Ф., Лафламм Р., Моска М. Введение в квантовые вычисления //Учеб. пособие/Ф. Кайе, Р. Лафламм Ижевск: РХД. – 2009.

[41] Башкиров, Е.К. Перепутывание двух сверхпроводящих кубитов, взаимодействующих с двухмодовым тепловым полем / Е.К. Башкиров, М.С.Мастюгин // Компьютерная оптика. - 2013. - Т.37, № 3. - С. 278-285.

[42] Башкиров Евгений Константинович, Литвинова Дарья Вадимовна Перепутывание кубитов при наличии атомной когерентности // КО. 2014. №4 С.663-669.

Приложение

Программа, для выполнения математического моделирования:

КВАНТОВАНИЕ СОСТОЯНИЙ ЭЛЕКТРОНА В КАНАЛЕ ПОЛЕВОГО ТРАНЗИСТОРА

Выпускная квалификационная работа

Выполнил студент 4 курса

Орищенко Никита Сергеевич

____________

Научный руководитель

к.ф. – м.н., доцент

Цирова И.С.

____________

Допустить к защите

Зав. кафедрой общей

теоретической физики

д. ф. – м. н., профессор

Бирюков А.А.

___________

«__» _______ 2017 г.

Самара 2017

Оглавление

Введение. 3

Глава 1. Модель Джейнса-Каммингса. Кубит. 7

1.1. Модель Джейнса-Каммингса. 7

1.2. Кубит. 10

1.2.1. Матрица плотности чистого состояния. 11

1.2.2. Матрица плотности смешанного состояния. 12

1.2.3. Матрица плотности кубита. 12

Глава 2. Сверхпроводящие кубиты.. 14

2.1. Свойства сверхпроводников. 14

2.2. Эффект Брайана Джозефсона. 17

2.3. Сверхпроводящие кубиты.. 19

Глава 3. Влияние диполь-дипольного взаимодействия на динамику двухкубитного перепутанного состояния. 22

Заключение. 28

Библиографический список. 29

Приложение. 34

Введение

В начале 2000-х годов была выдвинута гипотеза о возможности использования так называемых "искусственных" атомов (сверхпроводящие джозефсоновские кольца, квантовые точки, примесные спины и т.д.), для создания новых уникальных квантовых приборов, таких как квантовый компьютер, квантовая сеть, одноэлектронный транзистор и т.д. Наиболее востребованными для практического применения "искусственными" атомами являются сверхпроводящие джозефсоновские кубиты.

Следующим шагом стали эксперименты, описанные в статьях [3]-[11], с различными видами искусственных атомов, которые активно проводятся последние 10 лет. В России сотрудники Московского физико-технического института, Российского квантового центра, Национального исследовательского технологического университета МИСиС, Института физики твердого тела РАН и ряда других организаций под руководством Олега Астафьева, Алексея Устинова и Валерия Рязанова смогли впервые получить сверхпроводящий кубит в 2015 году. В настоящее время в различных странах реализуются долгосрочные программы [12]-[18] по использованию искусственных атомов для создания различных квантовых приборов для квантовых вычислений, квантовых телекоммуникаций и т.д. В частности, в работе [18] представлена программа работ по реализации протоколов квантовой криптографии между космическим спутником и наземной станции.

Однако, для работы квантовых приборов, базирующихся на использовании "искусственных" атомов (нейтральных атомов, ионов, сверхпроводящих кубитов, квантовых точек и т.д.) необходимо использовать перепутанные состояния таких объектов. В настоящее время проведено большое количество экспериментов [3]-[11], в которых были реализованы перепутанные состояния для различных искусственных атомов, а также разработаны эффективные схемы управления и контроля степени их перепутанности.

Перепутанные состояния [15] это основная составляющая квантовой информатики, они будут широко использованы для квантовой телепортации и коммуникаций, для решения вычислительных задач, связанных с многочастичными системами и т.д. Для управления перепутанных естественных и искусственных атомов используют их взаимодействие с классическими, квантовыми электромагнитным полями и другими бозонными полями [16]-[24].

Для теоретического описания таких систем используется Модель Джейнса-Каммингса и ее обобщения [4], [9]-[13]. Но для создания квантовых приборов наиболее интересными являются многокубитные системы. В таком случае при теоретическом описании удобнее пользоваться моделью Тависа-Каммингса. С ее помощью можно более полно описать особенности перепутывания, в следствие взаимодействия различных полей с атомами. Модели многокубитных систем [8] на сегодняшний день, вызывают наибольший интерес из-за возможности аналитически описать квантовые эффекты взаимодействия излучения и вещества [28], а также их практическую реализацию. Изучение перепутанных состояний в многокубитных системах является приоритетной задачей квантовой информатики и лазерной физики в связи с практическими потребностями физики квантовых вычислений, создания квантовых сетей и др.

При взаимодейств