Непосредственное интегрирование
Примеры:Найти интегралы
1) 
;
2) 
;
3) 
;
4) 
;
5) 
;
6) 
;
7) 
;
8) 
;
9) 
10) 
11) 
;
12) 
Замена переменных
1) 
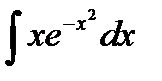
Положим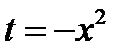 
. Продифференцируем обе части полученного равенства 
; 
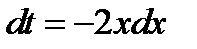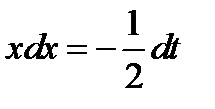
Тогда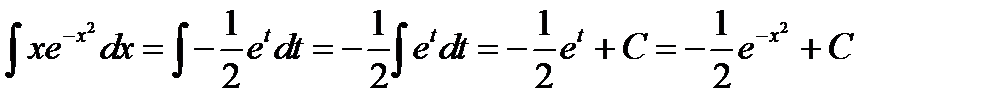 
2) 
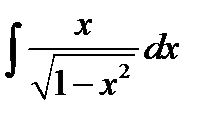. Положим 
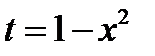. Продифференцируем обе части полученного равенства ;
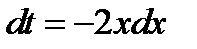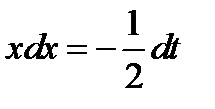
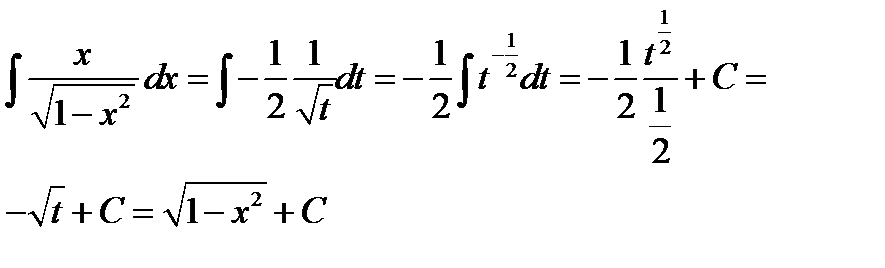
3) 
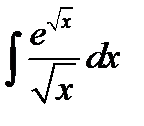Положим 
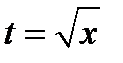. Продифференцируем обе части полученного равенства 
; 
;
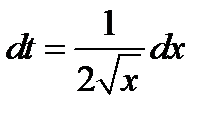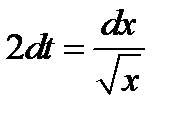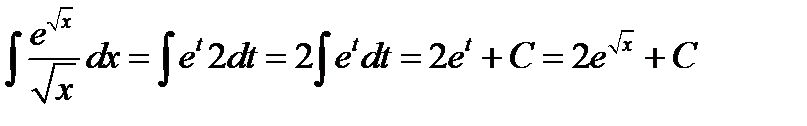
4) 
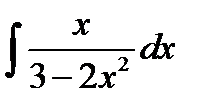; Положим 
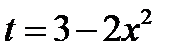. Продифференцируем обе части полученного равенства 
; 
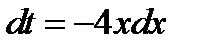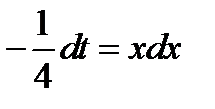
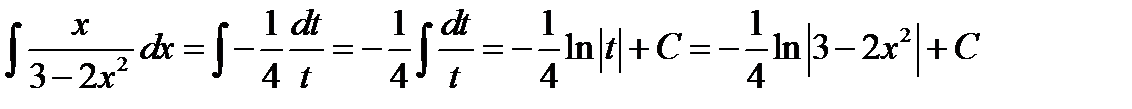
5) 
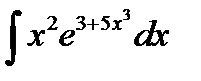. Положим 
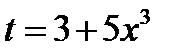. Продифференцируем обе части полученного равенства 
; 
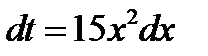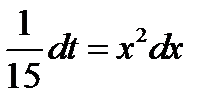
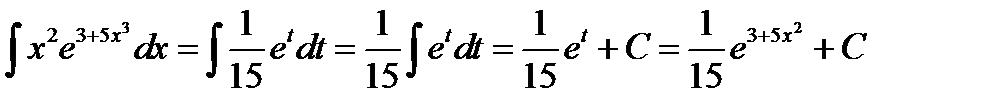
6) 
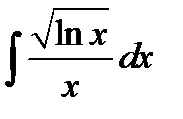. Положим 
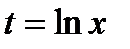. Продифференцируем обе части полученного равенства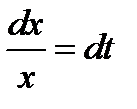 
;
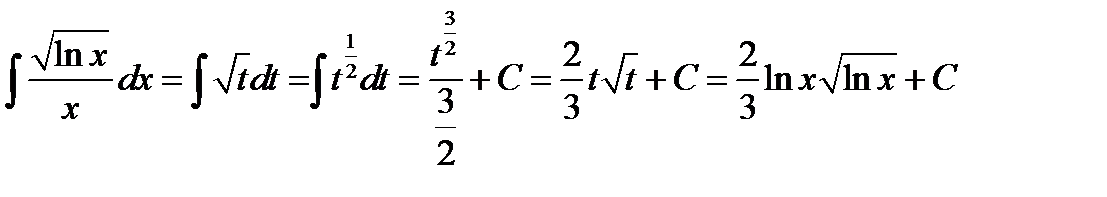7) 
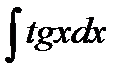
Так как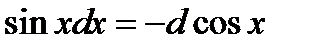 
, то 
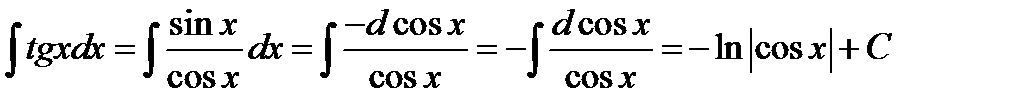
или:
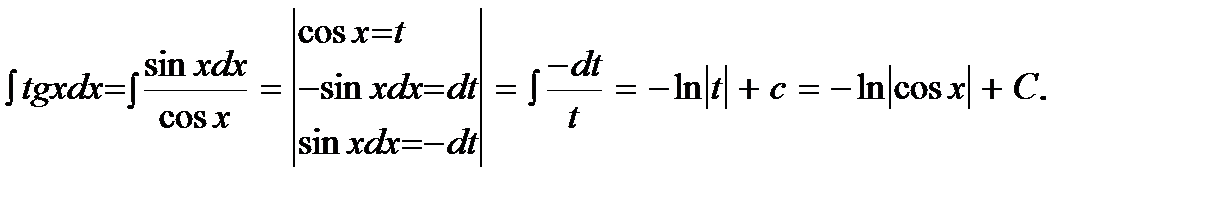
8) 
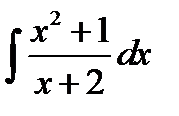
Положим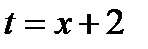 
. Тогда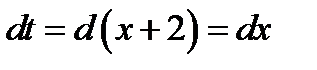 
Так как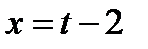 
, то
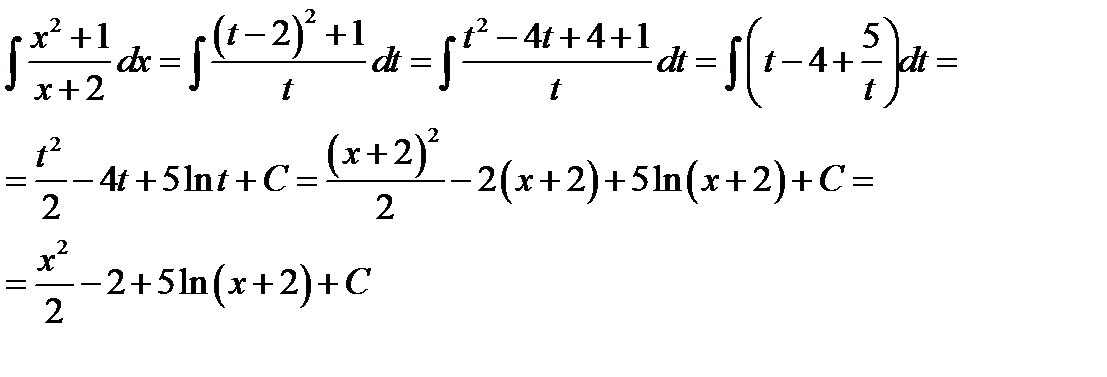
9) 
= 
= 
= 
= 
= 
= 
.
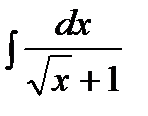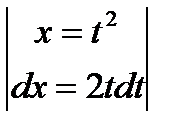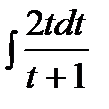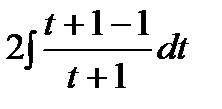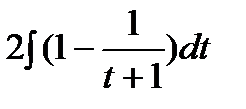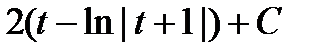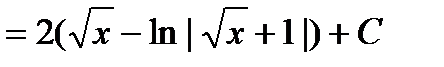10) 
= 
= 
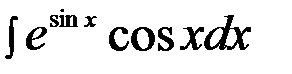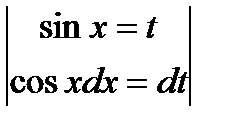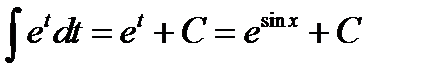
11) 
.
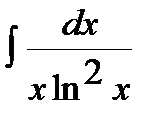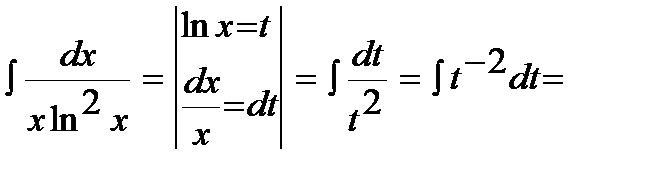
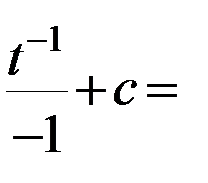
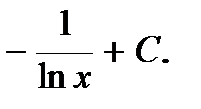
12) 
.
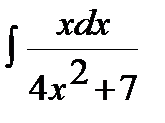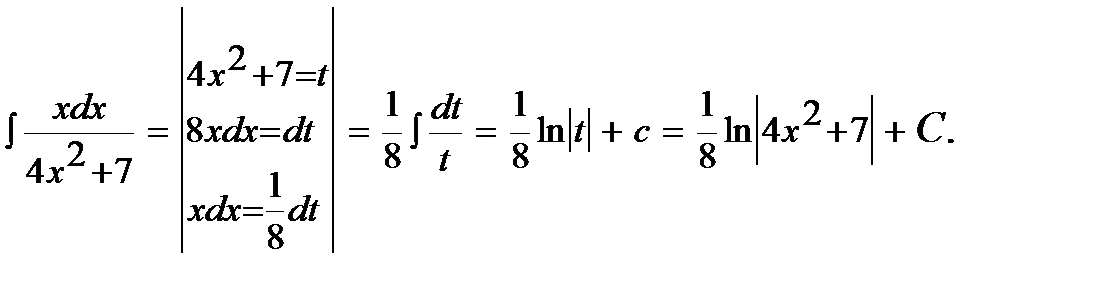
Интегрирование по частям в неопределенном интеграле.
Пример1:
= 
= 
=
= 
= 
.
Пример2:
= 
= 
= 
= 
= 
.
Пример 3:
= 
= 
= 
.
Пример4:
I= 
= 
= 
= 
= 
.
Последний интеграл есть не что иное как исходный интеграл, поэтому можно
записать:
; 
; 
.
Пример 5: 
=
= 
= 
=
= 
Пример 6.
.
Пример 7.
. Положим
Отсюда 
Пример 8.
. Выполним сначала замену переменной, положим
.
Тогда 
и 
. Следовательно,
,
Пусть 
, 
. Тогда 
,
и, применяя формулу интегрирования по частям, получаем:
.
Полагая в формуле интегрирования по частям 
, 
, получаем 
. Окончательно имеем
Итак, 
.
Пример 9. 
.
Положим 
Тогда 
и, следовательно, применяя формулу интегрирования по частям получим 
Интеграл 
вычислим отдельно, интегрируя его по частям.
Положив 
, находим: 
Следовательно, 
.
Но тогда 
Пример 10. 
Положим
Тогда
вычислим, используя метод разложения 
Таким образом, получаем:
Пример 11. 
Положим
Тогда 
Вычислим полученный интеграл методом подстановки. Положим
, тогда
,
Итак, 
.
Пример 12. 
Тогда 
Интегрирование функций, содержащих квадратный трехчлен
Примеры:
1) 
2) 
3) 
4) 
5) 
6) 
7) 
.
8) 
9) 
10) 
11) 
Поскольку 
, то используем замену переменной 
, 
Интегрирование рациональных функций.
Пример 1. Найти 
.
Поскольку рациональная дробь, стоящая под знаком интеграла, является неправильной, то представим ее в виде суммы многочлена и правильной дроби, для этого достаточно найти частное и остаток от деления числителя на знаменатель.
Тогда 
Разложим дробь 
на простейшие дроби:
;
Отсюда 
Следовательно,
Но тогда: 
= 
Пример 2. Найти 
Решение: Подынтегральную правильную рациональную дробь разложим на сумму простейших дробей:
.
Приведем правую часть к общему знаменателю 
и запишем тождественное равенство числителей:
.
Подставляя в полученное выражение корни знаменателя 
, 
, 
, найдем неизвестные коэффициенты 
:
Следовательно, искомый интеграл представим в виде:
Пример 3. Найти 
Подынтегральную правильную рациональную дробь раскладываем на сумму простейших:
.
Приводим к общему знаменателю и приравниваем числители:
.
Подставляя два действительных корня 
в полученное равенство, найдем неопределенные коэффициенты 
:
Для нахождения 
и 
в этом же равенстве приравняем коэффициенты при одинаковых степенях 
:
Решаем систему линейных уравнений:
Следовательно, искомый интеграл
Пример 4. Найти интеграл 
. 
.
Пример 5. Найти интеграл 
;
б) 
; в) 
.
найдём разложение подынтегральной функции 
на сумму простых дробей.
;
;
; 
Таким образом, 
.