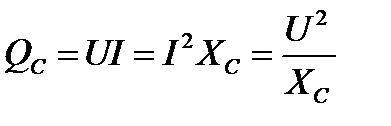Лекция № 2 ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА

1.Основные параметры, характеризующие синусоидальные токи, напряжения и ЭДС

2. Идеальные резистивный, индуктивный и емкостный элементы в цепях синусоидального тока

1. Основные параметры, характеризующие синусоидальные токи, напряжения и ЭДС

Токи, напряжения и ЭДС, значения которых периодически изменяются во времени по синусоидальному закону, называют синусоидальными (гармоническими).

По сравнению с постоянным током синусоидальный имеет ряд преимуществ:

производство, передача и использование электрической энергии наиболее экономичны при синусоидальном токе;

в цепях синусоидального тока относительно просто преобразовывать форму напряжения, а также создавать трехфазные системы напряжения.

В зависимости от типа решаемой задачи синусоидальные величины представляют:

- в виде аналитических выражений;
- графически, посредством временной или векторной диаграмм;

Аналитическое представление синусоидальных величин

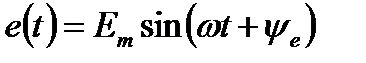Синусоидальные ЭДС, напряжение и ток можно задать с помощью вещественных функций времени (в виде аналитических выражений):

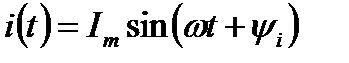
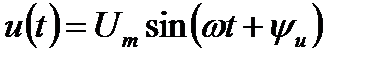
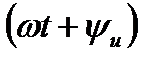где е, u, i - соответственно мгновенные значения ЭДС, напряжения, тока;
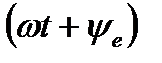
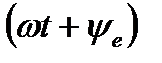- аргументы (фазы) синусоидальных

функций.

Для расчета электрических цепей аналитические выражения синусоидальных величин неудобны, т. к. алгебраические действия (сложение, вычитание, умножение и т. д.) с тригонометрическими функциями приводят к громоздким вычислениям.

Временная диаграмма

Графическое представление синусоидальных величин в виде временной диаграммы достаточно наглядно,

I2

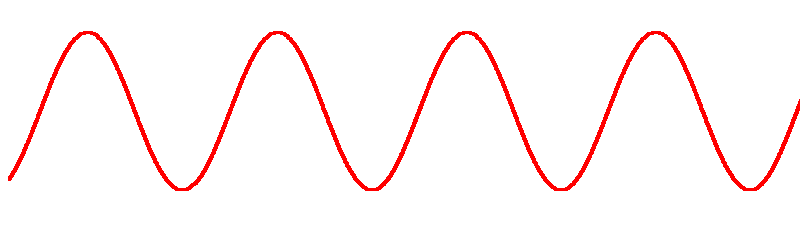
но из-за сложности построения синусоид и операций с ними применяется сравнительно редко.

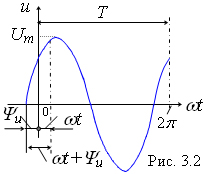
При построении временной диаграммы за аргумент синусоидальной функции, например, напряжения u(t) принимают время t или угол ωt .

Однако для большей наглядности угол φu часто выражают в градусах. Тогда аргумент ωt также переводят в градусы (напомним, что 1 рад » 57,3°). В этом случае период составляет 360°.

Основные параметры синусоидальных величин

Для характеристики синусоидальных функций времени используют следующие параметры:

- Мгновенное значение;
- Амплитуда;
- Период;
- Частота;
- Фаза;
- Начальная фаза;
- Угловая частота;
- Сдвиг фаз;
- Среднее значение гармонической функции;
- Действующее значение гармонической функции.

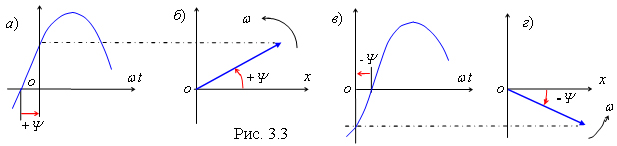
Цепь с активным сопротивлением

Элементы, обладающие активным сопротивлением R, нагреваются при прохождении через них тока.

Если к активному сопротивлению приложено синусоидальное напряжение

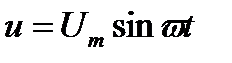
то и ток изменяется по синусоидальному закону

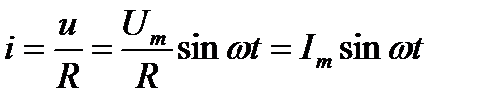
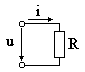
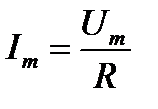где

или в действующих значениях

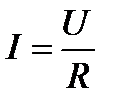
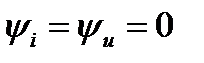Ток в цепи с активным сопротивлением совпадает по фазе с напряжением, т.к. их начальные фазы равны

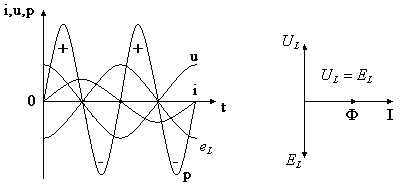
Временная и векторная диаграммы

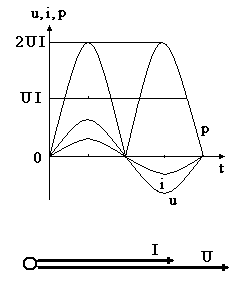
Активная мощность

Из временной диаграммы следует, что мощность в цепи с активным сопротивлением изменяется по величине, но не изменяется по направлению.

Эта мощность (энергия) необратима.

От источника она поступает к потребителю и полностью преобразуется в другие виды мощности (энергии), т.е. потребляется.

Такая потребляемая мощность называется активной.

Поэтому и сопротивление R, на котором происходит подобное преобразование, называется активным.

Количественно мощность в цепи с активным сопротивлением определяется

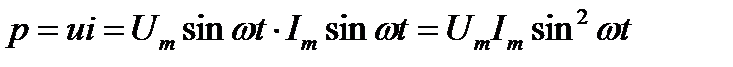
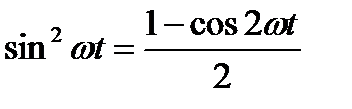
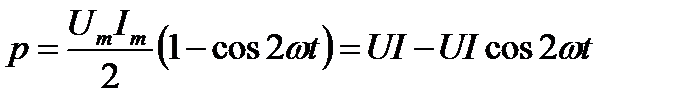
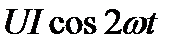
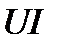Мгновенная мощность в цепи синусоидального тока с активным сопротивлением представляет собой сумму двух величин – постоянной мощности и переменной мощности , изменяющейся с двойной частотой

Среднее за период значение переменной составляющей

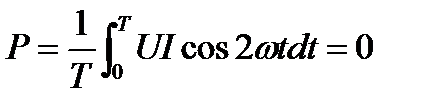
Таким образом, величина активной мощности в цепи синусоидального тока с активным сопротивлением с учётом закона Ома

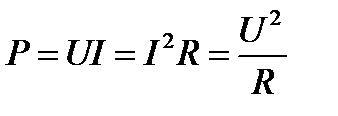
Единица активной мощности

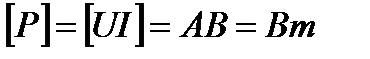
Цепь с идеальной индуктивностью

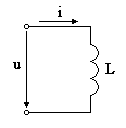Идеальной называют индуктивность такой катушки, активным сопротивлением и ёмкостью которой можно пренебречь

Если в цепи идеальной катушки проходит синусоидальный ток

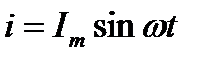
то он создаёт в катушке синусоидальный магнитный поток

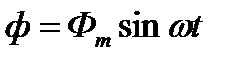
Этот поток индуцирует в катушке ЭДС самоиндукции

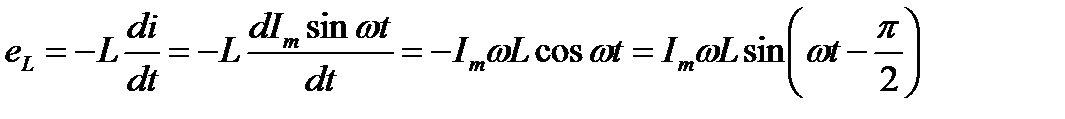
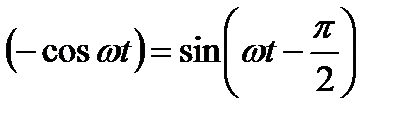
так как

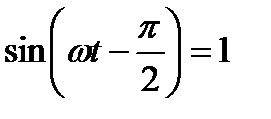
Эта ЭДС достигает амплитудного значения при

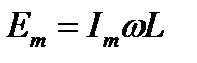
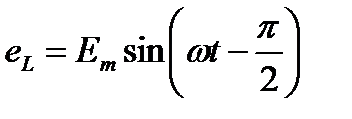Тогда

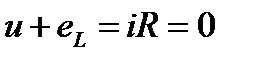ЭДС самоиндукции в цепи с идеальной индуктивностью, как и ток, вызвавший эту ЭДС, изменяется по синусоидальному закону, но отстаёт от тока по фазе на угол π/2.

Согласно второго закона Кирхгофа для мгновенных значений

Тогда напряжение, приложенное к цепи с идеальной индуктивностью

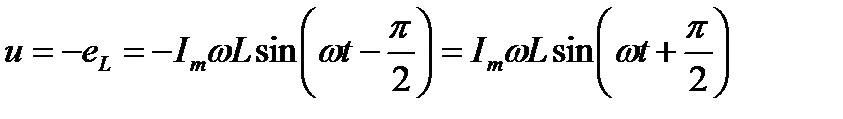
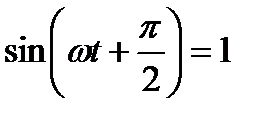Для существования тока в цепи с идеальной индуктивностью необходимо приложить к цепи напряжение, которое в любой момент времени равно по величине, но находится в противофазе с ЭДС, вызванной этим током

Напряжение достигает своего амплитудного значения при

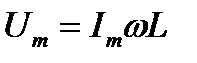
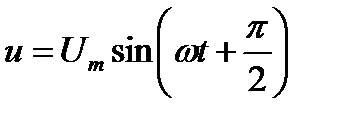Следовательно,

Напряжение, приложенное к цепи с идеальной индуктивностью, как и ток в этой цепи, изменяется по синусоидальному закону, но опережает ток по фазе на угол π/2.

Математическое выражение закона Ома для цепи синусоидального тока с идеальной индуктивностью

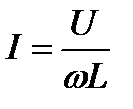
Знаменатель уравнения – индуктивное сопротивление

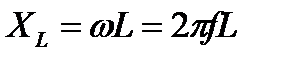
Тогда закон Ома будет иметь вид

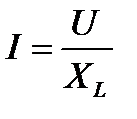
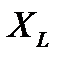
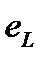Индуктивное сопротивление – это противодействие, которое ЭДС самоиндукции оказывает изменению тока.

Реактивная мощность в цепи с индуктивностью

Мгновенная мощность для цепи с идеальной катушкой индуктивности определяется

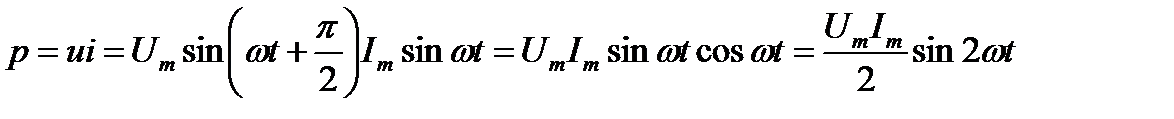
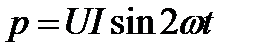Следовательно,

Мощность в цепи синусоидального тока с идеальной катушкой индуктивности изменяется по синусоидальному закону с двойной частотой

Среднее значение этой мощности за период, т.е. активная потребляемая мощность, равно нулю.

В 1-ю и 3-ю четверти периода мощность источника накапливается в магнитном поле индуктивности, а во 2-ю и 4-ю – возвращается к источнику.

В цепи переменного тока с идеальной катушкой мощность не потребляется, а колеблется между источником и катушкой индуктивности, загружая источник и провода

Такая колеблющаяся мощность, в отличие от активной, называется реактивной.

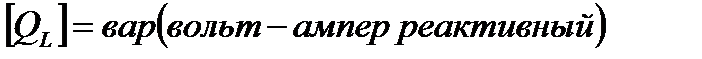
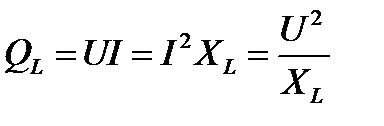
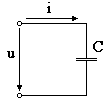
Цепь с ёмкостью

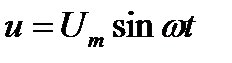Если к конденсатору ёмкостью С приложено синусоидальное напряжение

то в цепи конденсатора проходит ток

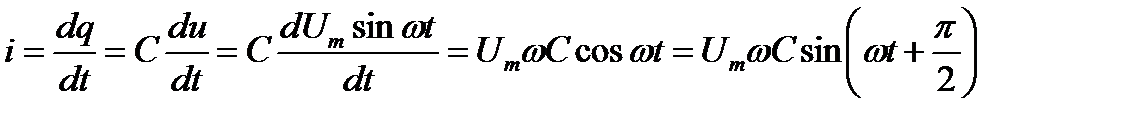
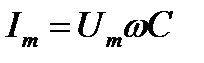
Амплитудное значении тока , следовательно

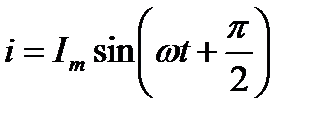
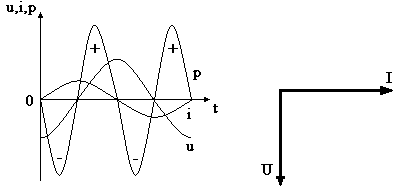
Ток в цепи конденсатора, как и напряжение, приложенное к его обкладкам, изменяется по синусоидальному закону, однако опережает это напряжение по фазе на угол π/2.

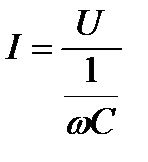
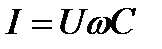Математическое выражение закона Ома для цепи переменного тока с ёмкостью

или

Знаменатель этого выражения является ёмкостным сопротивлением

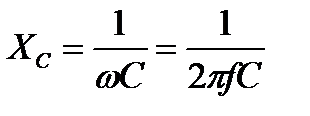
Тогда выражение для закона Ома будет иметь вид

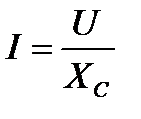
Ёмкостное сопротивление - это противодействие, которое оказывает напряжение заряженного конденсатора напряжению, приложенному к нему.

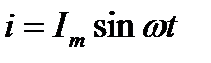Реактивная мощность в цепи с идеальным конденсатором

Если в цепи с идеальным конденсатором проходит ток , то

напряжение, приложенное к этому конденсатору будет

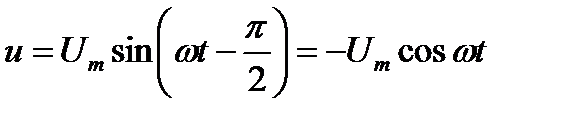
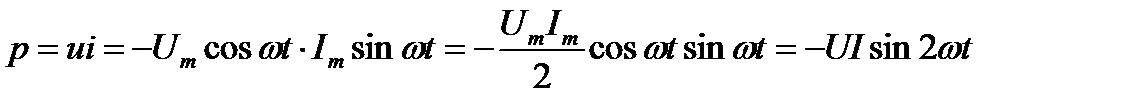Мгновенная мощность в цепи с конденсатором

Мощность в цепи с конденсатором, подключённым к источнику с синусоидальным напряжением, изменяется по синусоидальному закону с двойной частотой.

Во 2-ю и 4-ю четверти периода мощность источника накапливается в электрическом поле конденсатора. В 1-ю и 3-ю четверти эта мощность из электрического поля конденсатора возвращается к источнику.

В цепи переменного тока с конденсатором происходит колебание мощности между источником и конденсатором.

Величина реактивной мощности в цепи с конденсатором