Второй закон термодинамики. Энтропия.

Второй закон связан с понятием энтропии, являющейся мерой хаоса (или мерой порядка). Второй закон термодинамики гласит, что для вселенной в целом энтропия возрастает.

Существует два классических определения второго закона термодинамики :

• Кельвина и Планка

Не существует циклического процесса, который извлекает количество теплоты из резервуара при определенной температуре и полностью превращает эту теплоту в работу. (Невозможно построить периодически действующую машину, которая не производит ничего другого, кроме поднятия груза и охлаждения резервуара теплоты)

• Клаузиуса

Не существует процесса, единственным результатом которого является передача количества теплоты от менее нагретого тела к более нагретому. (Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара)

Оба определения второго закона термодинамики опираются на первый закон термодинамики, утверждающий, что энергия убывает.

Второй закон связан с понятием энтропии (S).

Энтропия порождается всеми процессами, она связана с потерей системы способности совершать работу. Рост энтропии - стихийный процесс. Если объем и энергия системы постоянны, то любое измение в системе увеличивает энтропию. Если же объем или энергия системы меняются, энтропия системы уменьшается. Однако, энтропия вселенной при этом не уменьшается.

Для того, чтобы энергию можно было использовать, в системе должны быть области с высоким и низким уровнями энергии. Полезная работа производится в результате передачи энергии от области с высоким уровнем энергии к области с низким уровнем энергии.

• 100% энергии не может быть преобразовано в работу
• Энтропия может вырабатываться, но не может быть уничтожена

Эффективность теплового двигателя

Эффективность теплового двигателя, действующего между двумя энергетическими уровнями , определена в пересчете на абсолютные температуры

η = ( T_h - T_c ) / T_h = 1 - T_c / T_h

где

η = эффективность

T_h = верхняя граница температуры (K)

T_c = нижняя граница температуры (K)

Для того, чтобы достичь максимальной эффективности T_c должна быть на столько низкой, на сколько это возможно. Чтобы эффект был 100% -м, T_cдолжна равнятся 0 по шкале Kельвина. Практически это невозможно, поэтому эффективность всегда меньше 1 (менее 100%).

• Изменение энтропии > 0
  Необратимыйпроцесс
• Изменение энтропии= 0
  Двустороннийпроцесс (обратимый)
• Изменение энтропии < 0
  Невозможный процесс (неосуществимый)

Энтропия определяет относительную способность одной системы влиять на другую. Когда энергия двигается к нижнему энергетическому уровню, где уменьшается возможность влияния на окружающую среду, энтропия увеличивается.

Определение энтропии

Энтропия определяется как :

S = H / T

где

S = энтропия (кДж/кг*К)

H = энтальпия (кДж/кг)

T = абсолютная температура (K)

Изменение энтропии системы вызвано изменением содержания темпла в ней. Изменение энтропии равно изменению темпла системы деленной на среднюю абсолютную температуру ( T_a):

dS = dH / T_a

Сумма значений (H / T) для каждого полного цикла Карно равна 0. Это происходит из-за того, что каждому положительному H противостоит отрицательное значение H.

• Тепловой цикл Карно

Цикл Карно— идеальный термодинамический цикл.

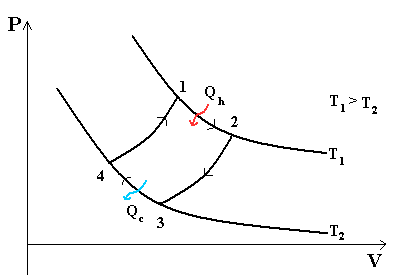
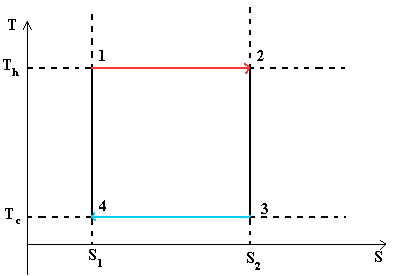
В тепловом двигателе, газ (реверсивно) нагревается (reversibly heated), а затем охлаждается. Модель цика следующая: Положение 1 --( изотермическое расширение) --> Положение 2 --( адиабатическое расширение) --> Положение 3 --(изотермическое сжатие) --> Положение 4 --(адиабатическое сжатие) --> Положение 1

Положение 1 - Положение 2: Изотермическое расширение
Изотермическое расширение. В начале процесса рабочее тело имеет температуру T_h , то есть температуру нагревателя. Затем тело приводится в контакт с нагревателем, который изотермически (при постоянной температуре) передаёт ему количество теплоты Q_H. При этом объём рабочего тела увеличивается. Q_H=∫Tds=T_h (S₂-S₁) =T_h ΔS
Положение 2 - Положение 3: Адиабатическое расширение
Адиабатическое (изоэнтропическое) расширение. Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом его температура уменьшается до температуры холодильника.
Положение 3 - Положение 4: Изотермическое сжатие
Изотермическое сжатие. Рабочее тело, имеющее к тому времени температуру T_c, приводится в контакт с холодильником и начинает изотермически сжиматься, отдавая холодильнику количество теплоты Q_c. Q_c=T_c(S₂-S₁)=T_c ΔS
Положение 4 - Положение 1: Адиабатическое сжатие
Адиабатическое (изоэнтропическое) сжатие. Рабочее тело отсоединяется от холодильника и сжимается без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя.

При изотермических процессах температура остаётся постоянной, при адиабатических отсутствует теплообмен, а значит, сохраняется энтропия.

Поэтому цикл Карно удобно представить в координатах T и S (температура и энтропия).

Законы термодинамики были определены эмперическим путем (эксперементально). Второй закон термодинамики - это обощение экспериментов, связанных с энтропией. Известно, что dS системы плюс dS окружающей среды равно или больше 0.

• Энтропия адиабатически изолированной системы не меняется!

Пример - Энтропия при нагревании воды

Процесс нагревания 1 кг воды от 0 до 100^oC (273 до 373 K) при нормальных условиях.

Удельная энтальпия для воды при 0^oC = 0 кДж/кг (удельная - на единицу массы)

Удельная энтальпия для воды при 100^oC = 419 кДж/кг

Изменение удельной энтропии :

dS = dH / T_a

= ((419 кДж/кг) - (0 кДж/кг)) / ((273 К + 373 К)/2)

= 1.297 кДж/кг*К

Пример - Энтропия при испарении воды

Процесс превращения 1 кг воды при 100^oC (373 K) в насыщенный пар при 100^oC (373 K) при нормальных условиях.

Удельная энтальпия пара при 100^oC (373 K) до испарения = 0 кДж/кг

Удельная теплота парообразования 100^oC (373 K) при испарении = 2 258 кДж/кг

Изменение удельной энтропии:

dS = dH / T_a

= (2 258 - 0) / ((373 + 373)/2)

= 6.054 кДж/кг*К

Полное изменение удельной энтропии испарения воды - это сумма удельной энтропии воды (при 0^oC) плюс удельная энтропия пара (при температуре 100^oC).

8 Термический КПД

Степень совершенства преобразования теплоты в механическую работу в термодинамическом цикле двигателя оценивается термическим (или тепловым, или термодинамическим) коэффициентом полезного действия η_t.

Термический КПД

Отношение работы, совершенной в прямом обратимом термодинамическом цикле, к теплоте, сообщенной рабочему телу от внешних источников.

В общем случае

η_t = A_t/Q₁ = (Q₁ – Q₂)/Q₁,

где A_t – тепло, преобразованное в цикле в работу; Q₁ – тепло, подведённое в цикле к рабочему телу; Q₂ – тепло, отданное в цикле рабочим телом.

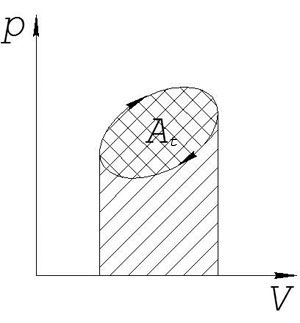Термический КПД

На индикаторной диаграмме это отношение площадей работы за цикл At (область заштрихованая «в клетку») и подведённой в цикле к рабочему телу теплоты Q1(вся заштрихованная область).

Термический КПД термодинамического цикла показывает, какое количество получаемой теплоты машина превращает в работу в конкретных условиях протекания идеального цикла. Чем больше величина η_t, тем совершеннее цикл и тепловая машина.

В качестве критерия оценки термодинамических циклов часто используют цикл Карно, потому что КПД тепловой машины Карно максимален в том смысле, что никакая тепловая машина с теми же температурами нагревателя и холодильника не может обладать бόльшим КПД [1]. Формула для расчёта термического КПД данного цикла общеизвестна

η_t = (T₁ – T₂)/T₁,

где T₁ – абсолютная температура нагревателя; T₂ – абсолютная температура холодильника.

Из анализа цикла Карно можно сделать следующие выводы:

1. КПД любого термодинамического цикла тем больше, чем больше разница температур нагревателя T₁ и холодильника T₂;

2. термический КПД никогда не достигает 100 %, потому что температура T₂ в лучшем случае равна температуре окружающей среды;

Сегодня наибольшая разница температур достигнута в двигателях внутреннего сгорания, благодаря высокой температуре рабочего тела T₁. Температура газов в цилиндре поршневого ДВС достигает 2000 °C и более, а в газовой турбине порядка 900 – 1300 °C, что связано с необходимость обеспечить жаропрочность лопаток турбины. Для двигателей с внешним подводом теплоты такие значения температур рабочего тела остаются пока недостижимыми из-за высокого термического сопротивления на границе нагреватель-рабочее тело. Температура пара в современных паровой турбине или поршневом паровом двигателе находится в диапазоне от 300 до 600 °C.

Стоит заметить, что высокий термический КПД не служит гарантией высокого эффективного КПД двигателя.

9.Тепрмодинамические процессы. Изохорный процесс.

Изохорический или изохорный процесс (от др.-греч. ἴσος — «равный» и χώρος — «место») — термодинамический процесс, который происходит при постоянном объёме. Для осуществления изохорного процесса в газе или жидкости достаточно нагревать (охлаждать) вещество в сосуде, который не изменяет своего объёма.

При изохорическом процессе давление идеального газа прямо пропорционально его температуре (см. Закон Шарля). В реальных газах закон Шарля не выполняется.

На графиках изображается линиями, которые называются изохоры. Для идеального газа они являются прямыми во всех диаграммах, которые связывают параметры: {\displaystyle T} (температура), {\displaystyle V} (объем) и {\displaystyle P} (давление).

Содержание

[скрыть]

• 1История
• 2Термодинамика процесса
• 3Энтропия при изохорном процессе
• 4Практическое применение теории изохорного процесса
• 5См. также
• 6Примечания
• 6.1Комментарии
• 6.2Источники
• 7Список литературы

История[править | править вики-текст]

Иллюстрация зависимости давления от температуры при постоянном объёме

Наиболее часто первые исследования изохорного процесса связывают с Гильомом Амптоном. В своей работе «Парижские мемуары» в 1702 году он описал поведение газа в фиксированном объёме^{[Комм 1]} внутри так называемого «воздушного термометра». Жидкость в нём находится в равновесии под воздействием давления газа в резервуаре и атмосферным давлением. При нагревании давление в резервуаре увеличивается, и жидкость вытесняется в выступающий столб. Зависимость между температурой и давлением была установлена в виде^{[1][Комм 2]}:

{\displaystyle {\frac {p_{1}}{p_{2}}}={\frac {1+\alpha t_{1}}{1+\alpha t_{2}}}}

В 1801 году Джон Дальтон в двух своих эссе опубликовал эксперимент, в котором установил, что все газы и пары, исследованные им при постоянном давлении, одинакового расширяются при изменении температуры, если начальная и конечная температура одинакова^[2][3]. Данный закон получил название закона Гей-Люссака, так как Гей-Люссак, вскоре провёл самостоятельные эксперименты и подтвердил одинаковое расширение различных газов, причём получив практически тот же самый коэффициент, что и Дальтон^[3]. Впоследствии он же объединил свой закон с законом Бойля — Мариотта^[4], что позволило описывать в том числе и изохорный процесс.

Термодинамика процесса[править | править вики-текст]

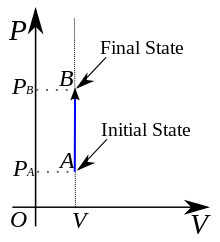
График изохорного процесса на диаграмме (P, V)

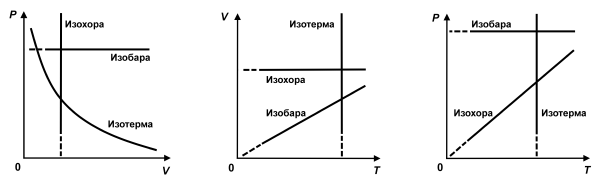
Графики изопроцессов в идеальном газе

Из определения работы следует, что изменение работы при термодинамическом процессе равно^[5]:

{\displaystyle \delta A=PdV}

Чтобы определить полную работу процесса проинтегрируем данное выражение^[5]:

{\displaystyle A=\int \limits _{V_{1}}^{V_{1}}PdV},

Но, поскольку объём неизменен, то такой интеграл равен нулю. Итак, при изохорном процессе газ работы не совершает^[6]:

{\displaystyle A=0}.

Это же можно показать на графике изохорного процесса. С математической точки зрения, работа процесса равна площади такого графика^[5]. Но график изохорного процесса является перпендикуляром к оси абсцисс. Таким образом, площадь под ним равна нулю.

Изменение внутренней энергии идеального газа можно найти по формуле^[7]:

{\displaystyle \Delta U={\frac {i}{2}}\nu R\Delta T},

где {\displaystyle i} — число степеней свободы, которое зависит от количества атомов в молекуле (3 — для одноатомной (например, неон), 5 — для двухатомной (например, кислород) и 6 — для трёхатомной и более (например, молекула водяного пара)).

Из определения и формулы теплоёмкости и, формулу для внутренней энергии можно переписать в виде^[7]:

{\displaystyle \Delta U=\nu c_{v}^{\mu }\Delta T},

где {\displaystyle c_{v}^{\mu }} — молярная теплоёмкость при постоянном объёме.

Используя первое начало термодинамики можно найти количество теплоты при термодинамическом процессе^[8]:

{\displaystyle Q=\Delta U+A}

Но при изохорном процессе газ не выполняет работу^[6]. То есть, имеет место равенство:

{\displaystyle Q=\Delta U=\nu c_{v}^{\mu }\Delta T},

таким образом, вся теплота, которую получает газ, идёт на изменение его внутренней энергии.

Энтропия при изохорном процессе[править | править вики-текст]

Поскольку в системе при изохорном процессе происходит теплообмен с внешней средой, то происходит изменение энтропии. Из определения энтропии следует^[9]:

{\displaystyle dS={dQ \over T}}

Выше была выведена формула для определения количества теплоты. Перепишем её в дифференциальном виде^{[10][Комм 3]}:

{\displaystyle dQ=\nu c_{v}^{\mu }dT,}

где {\displaystyle \nu } — количество вещества, {\displaystyle c_{v}^{\mu }} — молярная теплоемкость при постоянном объёме. Итак, микроскопическое изменение энтропии при изохорном процессе можно определить по формуле^[10]:

{\displaystyle dS={\nu c_{v}^{\mu }dT \over T}}

Или, если проинтегрировать последнее выражение, полное изменение энтропии в этом процессе^[10]:

{\displaystyle \int \limits _{S_{1}}^{S_{2}}dS=\nu \int \limits _{T_{1}}^{T_{2}}{c_{v}^{\mu }dT \over T}\Rightarrow \Delta S=\nu \int \limits _{T_{1}}^{T_{2}}{c_{v}^{\mu }dT \over T}}

В данном случае выносить выражение молярной теплоемкости при постоянном объёме за знак интеграла нельзя, поскольку она является функцией, которая зависит от температуры.

Практическое применение теории изохорного процесса[править | править вики-текст]

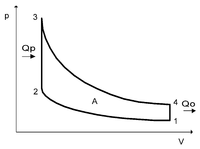
p—V диаграмма цикла Отто

Основные статьи: Цикл Отто, Адиабатический процесс

При идеальном цикле Отто, который приближённо воспроизведён в бензиновом двигателе внутреннего сгорания, такты 2—3 и 4—1 являются изохорными процессами. Работа, совершаемая на выходе двигателя, равна разности работ, которую произведёт газ над поршнем во время третьего такта (то есть рабочего хода), и работы, которую затрачивает поршень на сжатие газа во время второго такта. Так как в цикле Отто используется система принудительного зажигания смеси, то происходит сжатие газа в 7—12 раз^[11]

10. Изобарный процесс

Изоба́рный проце́сс (др.-греч. ἴσος «одинаковый» и βάρος «тяжесть») — термодинамический процесс, происходящий в системе при постоянном давлении и постоянной массе газа.

Согласно закону Гей-Люссака, при изобарном процессе в идеальном газе {\displaystyle {\frac {V}{T}}=\mathrm {const} .}

Если использовать уравнение Клапейрона — Менделеева, то работа, совершаемая газом при расширении или сжатии газа, равна {\displaystyle A={\frac {m}{M}}R(T_{2}-T_{1})}

Количество теплоты, получаемое или отдаваемое газом, характеризуется изменением энтальпии: {\displaystyle \delta Q=\Delta I=\Delta U+P\Delta V.}

Содержание

[скрыть]

• 1Теплоёмкость
• 2Изменение энтропии
• 3Литература
• 4См. также

Теплоёмкость[править | править вики-текст]

Молярная теплоёмкость при постоянном давлении обозначается как {\displaystyle C_{p}.} В идеальном газе она связана с теплоёмкостью при постоянном объёме соотношением Майера {\displaystyle C_{p}=C_{v}+R.}

Молекулярно-кинетическая теория позволяет вычислить приблизительные значения молярной теплоёмкости для различных газов через значение универсальной газовой постоянной R:

• для одноатомных газов {\displaystyle C_{p}={\frac {5}{2}}R}, то есть около 20,8 Дж/(моль·К);
• для двухатомных газов {\displaystyle C_{p}={\frac {7}{2}}R}, то есть около 29,1 Дж/(моль·К);
• для многоатомных газов {\displaystyle C_{p}=4R}, то есть около 33,3 Дж/(моль·К).

Теплоёмкости можно также определить исходя из уравнения Майера, если известен показатель адиабаты, который можно измерить экспериментально (например, с помощью измерения скорости звука в газе или используя метод Клемана — Дезорма).

Изменение энтропии[править | править вики-текст]

Изменение энтропии при квазистатическом изобарном процессе равно {\displaystyle \Delta S=\int \limits _{1}^{2}{\frac {dQ}{T}}.} В случае, если изобарный процесс происходит в идеальном газе, то {\displaystyle dQ=d(\nu C_{v}T+\nu RT)=\nu (C_{v}+R)dT=\nu C_{p}dT,} следовательно, изменение энтропии можно выразить как {\displaystyle \Delta S=\int \limits _{T_{1}}^{T_{2}}\nu C_{p}{\frac {dT}{T}}.} Если пренебречь зависимостью {\displaystyle C_{p}} от температуры (это предположение справедливо, например, для идеального одноатомного газа, но в общем случае не выполняется), то {\displaystyle \Delta S=\nu C_{p}\ln {\frac {T_{2}}{T_{1}}}.}

11. Изотермический процесс

Изотермический процесс (от др.-греч. ἴσος «равный» и θέρμη «жар») — термодинамический процесс, происходящий в физической системе при постоянной температуре.

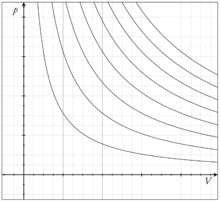
Несколько изотерм для идеального газа нa p-V диаграмме

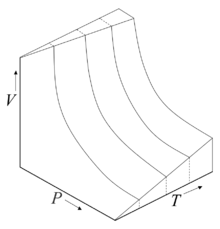
Несколько изотерм для идеального газа нa p-V-T диаграмме

Для осуществления изотермического процесса систему обычно помещают в термостат (массивное тело, находящееся в тепловом равновесии), теплопроводность которого велика, так что теплообмен с системой происходит достаточно быстро по сравнению со скоростью протекания процесса, и, температура системы в любой момент практически не отличается от температуры термостата. Можно осуществить изотермический процесс иначе — с применением источников или стоков тепла, контролируя постоянство температуры с помощью термометров. К изотермическим процессам относятся, например, кипение жидкости или плавление твёрдого тела при постоянном давлении. Графиком изотермического процесса является изотерма.

В идеальном газе при изотермическом процессе для неизменной массы газа произведение давления на объём постоянно (закон Бойля-Мариотта). Изотермы идеального газа в координатах {\displaystyle p,V} — гиперболы, расположенные на графике тем выше, чем выше температура, при которой происходит процесс (см. рисунок).

В общем случае при изотермическом процессе системе сообщается некоторое количество теплоты {\displaystyle Q} (или она отдаёт теплоту) и системой совершается работа {\displaystyle A} над внешними телами. Альтернативный процесс, при котором теплообмен с окружающей средой отсутствует (термодинамическая система находится в энергетическом равновесии — система не поглощает и не выделяет тепло), называется адиабатическим процессом.

Работа {\displaystyle A}, совершённая идеальным газом в изотермическом процессе, равна {\displaystyle N\,k\,T\,\ln(V_{2}/V_{1})}, где {\displaystyle N} — число частиц газа, {\displaystyle T} — температура, {\displaystyle V_{1}} и {\displaystyle V_{2}} — объём газа в начале и конце процесса, {\displaystyle k} — постоянная Больцмана .

В твёрдом теле и большинстве жидкостей изотермические процессы очень мало изменяют объём тела, если только не происходит фазовый переход.

Первый закон термодинамики для изотермического процесса записывается в виде:

{\displaystyle Q=A,}

где учитывается, что внутренняя энергия системы в изотермическом процессе не изменяется. Таким образом, в изотермическом процессе вся теплота, полученная системой, расходуется на совершение системой работы над внешними телами.

Это заготовка статьи по физике. Вы можете помочь проекту, дополнив её.

12. Адиабатный процесс

Адиабати́ческий, или адиаба́тный проце́сс (от др.-греч. ἀδιάβατος — «непроходимый») — термодинамический процесс в макроскопической системе, при котором система не обменивается теплотой с окружающим пространством. Серьёзное исследование адиабатических процессов началось в XVIII веке^[1].

Адиабатический процесс является частным случаем политропного процесса, так как при нём теплоёмкость газа равна нулю и, следовательно, постоянна^[2]. Адиабатические процессы обратимы только тогда, когда в каждый момент времени система остаётся равновесной (например, изменение состояния происходит достаточно медленно) и изменения энтропии не происходит. Некоторые авторы (в частности, Л. Д. Ландау) называли адиабатическими только обратимые адиабатические процессы^[3].

Обратимый адиабатический процесс для идеального газа описывается уравнением Пуассона. Линия, изображающая адиабатный процесс на термодинамической диаграмме, называется адиабатой Пуассона. Примером необратимого адиабатического процесса может быть распространение ударной волны в газе. Такой процесс описывается ударной адиабатой. Адиабатическими можно считать процессы в целом ряде явлений природы. Также такие процессы получили ряд применений в технике.

Содержание

[скрыть]

• 1История
• 2Физический смысл адиабатического процесса
• 2.1Работа газа
• 2.2Внутренняя энергия идеального газа
• 3Уравнение Пуассона для идеального газа
• 3.1Адиабата Пуассона
• 3.2Вывод уравнения
• 3.3Показатель адиабаты
• 4Энтропия и обратимость
• 5Примеры
• 5.1Цикл Карно
• 5.2Цикл Отто
• 5.3Прохождение звуковых волн в газе
• 5.4Сжижение газов
• 5.5Магнитное охлаждение
• 6См. также
• 7Примечания
• 7.1Комментарии
• 7.2Источники
• 8Литература

История[править | править вики-текст]

Уравнение Пуассона позволило описать адиабатический процесс

Существование атмосферного давления было показано рядом экспериментов в XVII веке. Одним из первых доказательств гипотезы стали магдебургские полушария, сконструированные немецким инженером Герике. Из сферы, образованной полушариями, выкачивался воздух, после чего их было трудно разъединить в силу внешнего давления воздуха. Другой эксперимент в рамках исследования природы атмосферного давления поставил Роберт Бойль. Он состоял в том, что если запаять изогнутую стеклянную трубку с короткого конца, а в длинное колено постоянно подливать ртуть, она не поднимется до верха короткого колена, поскольку воздух в трубке, сжимаясь, будет уравновешивать давление ртути на него. К 1662 году данные опыты позволили прийти к формулировке закона Бойля — Мариотта^[4].

В 1779 году в «Пирометрии» Ламберта был описан опыт повышения и понижения температуры в приёмнике воздушного насоса при движении поршня. Впоследствии данный эффект был подтверждён Дарвином (1788) и Пикте (1798). В 1802 году Дальтон опубликовал доклад, в котором, в числе прочего, указал, что сгущение газов сопровождается выделением тепла, а разрежение — охлаждением. Рабочий оружейного завода зажёг трут в дуле духового ружья путём сжатия воздуха, о чём сообщил в 1803 году лионский физик Моле^[1].

Теоретическим обобщением накопившихся экспериментальных знаний занялся физик Пуассон. Так как при адиабатическом процессе температура непостоянна, то закон Бойля — Мариотта требует поправки, которую Пуассон обозначил как коэффициент k и выразил через соотношение теплоёмкостей. Экспериментально данный коэффициент определялся Вальтером и Гей-Люссаком (эксперимент описан в 1807 году) и затем более точно Дезормом и Клеманом в 1819 году. Практическое использование адиабатического процесса предложил С. Карно в работе «Движущая сила огня» в 1824 году^[1].

Физический смысл адиабатического процесса[править | править вики-текст]

Если термодинамический процесс в общем случае представляет собой три процесса — теплообмен, совершение системой (или над системой) работы и изменение её внутренней энергии^[5], то адиабатический процесс в силу отсутствия теплообмена ({\displaystyle \Delta Q=0}) системы со средой сводится только к последним двум процессам^[6]. Поэтому первое начало термодинамики в этом случае приобретает вид^{[7][Комм 1]}

{\displaystyle \Delta U=-A,}

где {\displaystyle \Delta U} — изменение внутренней энергии тела, {\displaystyle A} — работа, совершаемая системой.

Изменения энтропии {\displaystyle S} системы в обратимом адиабатическом процессе вследствие передачи тепла через границы системы не происходит^[8]:

{\displaystyle \mathrm {d} S=\delta Q/T=0.}

Здесь {\displaystyle T} — температура системы, {\displaystyle \delta Q} — теплота, полученная системой. Благодаря этому адиабатический процесс может быть составной частью обратимого цикла^[8].

Работа газа[править | править вики-текст]

Основная статья: Термодинамическая работа

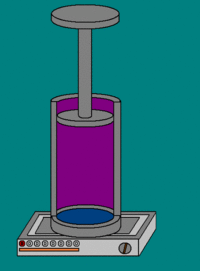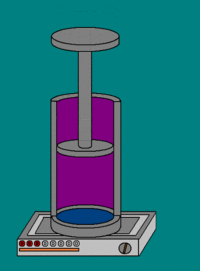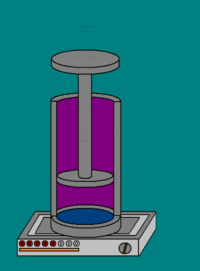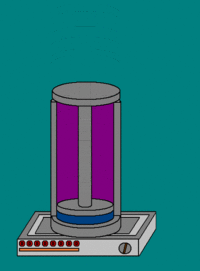
Совершение над газом работы на элементарном участке dh. Совершаемая работа показана красными лампочками

Поясним понятие работы применительно к адиабатическому процессу. В частном случае, когда работа совершается через изменение объёма, можно определить её следующим способом: пусть газ заключён в цилиндрический сосуд, плотно закрытый легко скользящим поршнем. Если газ будет расширяться, то он будет перемещать поршень и при перемещении на отрезок {\displaystyle \mathrm {d} h} совершать работу^[9][10]

{\displaystyle \mathrm {d} A=F\mathrm {d} h,}

где F — сила, с которой газ действует на поршень. Перепишем уравнение:

{\displaystyle \mathrm {d} A=ps\mathrm {d} h,}

где s — площадь поршня. Тогда работа будет равна^[9][10]

{\displaystyle \mathrm {d} A=p\mathrm {d} V,}

где {\displaystyle p} — давление газа, {\displaystyle \mathrm {d} V} — малое приращение объёма. Аналогично видно, что уравнение выполняется и для сосудов с произвольной поперечной формой сечения. Данное уравнение справедливо и при расширении на произвольных объёмах. Для этого достаточно разбить поверхность расширения на элементарные участки {\displaystyle dS}, на которых расширение одинаково^[9].

Основное уравнение термодинамики примет вид^[11]:

{\displaystyle \mathrm {d} U=-p\,\mathrm {d} V} (1)

Это условие будет выполняться, если скорость хода поршня (протекания процесса в общем случае) будет удовлетворять определённым условиям. С одной стороны, она должна быть достаточно малой, чтобы процесс можно было считать квазистатическим. Иначе при резком изменении хода поршня давление, которое его перемещает, будет отличаться от давления в целом по газу. То есть газ должен находиться в равновесии, без турбулентностей и неоднородностей давления и температуры. Для этого достаточно передвигать поршень со скоростью, существенно меньшей, чем скорость звука в данном газе. С другой стороны, скорость должна быть достаточно большой, чтобы можно было пренебречь обменом тепла с окружающей средой и процесс оставался адиабатическим^[12][13].

Однако работа может совершаться и другими путями — например, идти на преодоление межмолекулярного притяжения газов. В этом случае параллельно с изменением внутренней энергии будет происходить процессы совершения нескольких работ разной физической природы, и основное уравнение термодинамики примет вид:

{\displaystyle \mathrm {d} U=-\sum _{i}A_{i}\mathrm {d} a_{i},} (1a)

где {\displaystyle A_{i}}, {\displaystyle \mathrm {d} a_{i}} — дифференциальное выражение для работы, {\displaystyle a_{i}} — внешние параметры, которые меняются при совершении работы, {\displaystyle A_{i}} — соответствующие им внутренние параметры, которые при совершении малой работы можно считать постоянными. При совершении работы путём сжатия или расширения внутренний параметр — давление, внешний параметр — объём.

Внутренняя энергия идеального газа[править | править вики-текст]

Тепловое движение молекул одноатомного газа идёт в среднем тем интенсивнее, чем больше его внутренняя энергия. Скорость каждой отдельной молекулы при этом может изменяться даже при постоянстве внутренней энергии всего газа^{[Комм 2]}

Основная статья: Внутренняя энергия

Внутренняя энергия является однозначной функцией состояния системы. Поэтому применительно к адиабатическому процессу её изменение имеет тот же физический смысл, что и в общем случае. Согласно закону Джоуля, выведенному экспериментально, внутренняя энергия идеального газа не зависит от давления или объёма газа. Исходя из этого факта, можно получить выражение для изменения внутренней энергии идеального газа. По определению молярной теплоёмкости при постоянном объёме, {\displaystyle \left({\frac {\partial U}{\partial T}}\right)_{V}=C_{V}}^[14]. Иными словами — это предельное соотношение изменения внутренней энергии и породившего его изменения температуры. При этом, по определению частной производной считается только то изменение внутренней энергии, которое порождено именно изменением температуры, а не другими сопутствующими процессами. Так как внутренняя энергия идеального газа является функцией только температуры, то

{\displaystyle \mathrm {d} U=\nu C_{V}\mathrm {d} T,} (2)

где {\displaystyle \nu } — число молей идеального газа.

Уравнение Пуассона для идеального газа[править | править вики-текст]

У этого термина существуют и другие значения, см. Уравнение Пуассона.

Адиабата Пуассона[править | править вики-текст]

Для идеальных газов, чью теплоёмкость можно считать постоянной, в случае квазистатического процесса адиабата имеет простейший вид и определяется уравнением^[6][15][16]

{\displaystyle p\,\cdot V^{\mathsf {k}}=\mathrm {const} ,}

где {\displaystyle V} — его объём, {\displaystyle {\mathsf {k}}={\frac {C_{p}}{C_{V}}}} — показатель адиабаты, {\displaystyle C_{p}} и {\displaystyle C_{V}} — теплоёмкости газа соответственно при постоянном давлении и постоянном объёме.

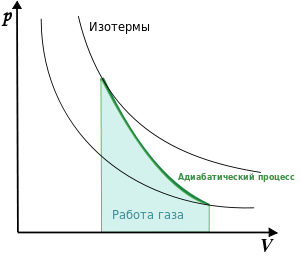
График адиабаты (жирная линия) на {\displaystyle p\circ V} диаграмме для газа.
{\displaystyle p} — давление газа;
{\displaystyle V} — объём

С учётом уравнения состояния идеального газа уравнение адиабаты может быть преобразовано к виду

{\displaystyle T^{\mathsf {k}}\cdot p^{(1-{\mathsf {k}})}=\mathrm {const} ,}

где {\displaystyle T} — абсолютная температура газа. Или к виду

{\displaystyle T\cdot V^{({\mathsf {k}}-1)}=\mathrm {const} .}

Поскольку {\displaystyle {\mathsf {k}}} всегда больше 1, из последнего уравнения следует, что при адиабатическом сжатии (то есть при уменьшении {\displaystyle V}) газ нагревается ({\displaystyle T} возрастает), а при расширении — охлаждается, что всегда верно и для реальных газов. Нагревание при сжатии больше для того газа, у которого больше коэффициент {\displaystyle {\mathsf {k}}}.

Вывод уравнения[править | править вики-текст]

Согласно закону Менделеева — Клапейрона^[6] для идеального газа справедливо соотношение

{\displaystyle pV=\nu RT,}

где R — универсальная газовая постоянная. Вычисляя полные дифференциалы от обеих частей уравнения, полагая независимыми термодинамическими переменными {\displaystyle \left(p,V,T\right)}, получаем

{\displaystyle p\mathrm {d} V+V\mathrm {d} p=\nu R\mathrm {d} T.} (3)

Если в (3) подставить {\displaystyle dT} из (2), а затем {\displaystyle dU} из (1), получим

{\displaystyle p\mathrm {d} V+V\mathrm {d} p=-p\mathrm {d} V\cdot {\frac {R}{C_{V}}},}

или, введя коэффициент {\displaystyle {\mathsf {k}}=1+R/C_{V}}:

{\displaystyle {\mathsf {k}}\,p\mathrm {d} V+V\mathrm {d} p=0.}

Это уравнение можно переписать в виде

{\displaystyle {\mathsf {k}}\,\mathrm {d} V/V=-\mathrm {d} p/p,}

что после интегрирования даёт:

{\displaystyle {\mathsf {k}}\,\ln V=-\ln p+\mathrm {const} .}

Потенцируя, получаем окончательно:

{\displaystyle p\,\cdot V^{\mathsf {k}}=\mathrm {const} ,}

что и является уравнением адиабатического процесса для идеального газа.

Показатель адиабаты[править | править вики-текст]

Основная статья: Показатель адиабаты

Показатели адиабаты для различных газов[17][18]
Темп.	Газ	k		Темп.	Газ	k
−181 °C	H2	1,597	20 °C	He	1,660
−76 °C	1,453	20 °C	H2O	1,330
20 °C	1,410	100 °C	1,324
100 °C	1,404	200 °C	1,310
400 °C	1,387	−180 °C	Ar	1,760
1000 °C	1,358	20 °C	1,670
2000 °C	1,318

При адиабатическом процессе показатель адиабаты равен {\displaystyle {\mathsf {k}}=\left(1+{\frac {R}{C_{V}}}\right).}

Для нерелятивистского невырожденного одноатомного идеального газа {\displaystyle {\mathsf {k}}=5/3}^[19], для двухатомного {\displaystyle {\mathsf {k}}=7/5}^[19], для трёхатомного {\displaystyle {\mathsf {k}}=4/3}, для газов, состоящих из более сложных молекул, показатель адиабаты {\displaystyle {\mathsf {k}}} определяется числом степеней свободы (i) конкретной молекулы, исходя из соотношения {\displaystyle i={\frac {2C_{V}}{R}}}.

Для реальных газов показатель адиабаты отличается от показателя адиабаты для идеальных газов, особенно при низких температурах, когда большу́ю роль начинает играть межмолекулярное взаимодействие. Для его теоретического нахождения следует проводить расчёт без некоторых допущений, в частности, использованных при выводе формулы (1), и использовать формулу (1а).

Один из методов для экспериментального определения показателя был предложен в 1819 г. Клеманом и Дезормом. Стеклянный баллон вместимостью несколько литров наполняется исследуемым газом при давлении {\displaystyle P_{1}}. Затем открывается кран, газ адиабатически расширяется, и давление падает до атмосферного — {\displaystyle P_{0}}. Затем происходит его изохорное нагревание до температуры окружающей среды. Давление повышается до {\displaystyle P_{2}}. В результате такого эксперимента k можно вычислить как^[20]

{\displaystyle {\mathsf {k}}={\frac {P_{1}-P_{0}}{P_{1}-P_{2}}}.}

Энтропия и обратимость[править | править вики-текст]

В общем случае для произвольной физической системы изменение состояния при адиабатическом расширении определяется производными термодинамических параметров при постоянной энтропии. Справедливы соотношения

{\displaystyle \left({\frac {\partial T}{\partial V}}\right)_{S}=-{\frac {T}{C_{V}}}\left({\frac {\partial p}{\partial T}}\right)_{V}},

{\displaystyle \left({\frac {\partial T}{\partial p}}\right)_{S}={\frac {T}{C_{p}}}\left({\frac {\partial V}{\partial T}}\right)_{p}},

где C_p и C_v — теплоёмкости при постоянном давлении и объёме, которые всегда положительны по своему ф