Квантовая красота IV: Доверяем красоте
Притча о додекаэдре
Додекаэдр уже появлялся несколько раз в нашей медитации. Будучи одним из пяти платоновых тел, он воплощает немало геометрической симметрии. Согласно самому Платону, это форма Вселенной в целом. Мы видели, как Сальвадор Дали использовал символизм додекаэдра, чтобы выразить космическое соединение, которое могло бы быть трудно перенести на холст иначе. Мы также нашли додекаэдр, скрывающийся в пределах каждого из бесконечного разнообразия фуллеренов, где его 12 пятиугольников обеспечивают шестиугольникам графена возможность образовать замкнутую поверхность.
У додекаэдров также есть одно очень практичное применение: в качестве настольного календаря. Они прекрасно подходят для этого, поскольку имеют 12 граней, совершенно одинаковых, так что вы можете поместить по месяцу на каждой. В Интернете легко можно найти инструкции, как сделать такие календари, вырезав их из жесткой бумаги или картона.
Додекаэдр – красивая вещь, и к настоящему времени он стал нам близким другом.
Теперь предположим, что некий игривый дух хочет проверить наш характер или дать нам радость решения милой головоломки. Он разъединяет части схемы и убирает метки, и мы получаем загадку, изображенную на илл. 39.
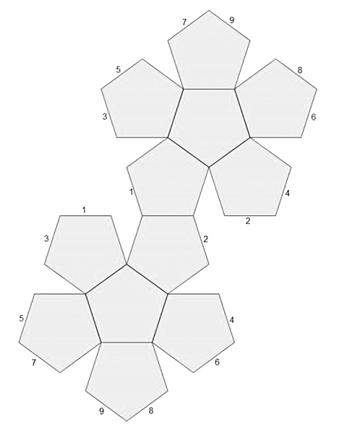
Илл. 38. Этот красивый чертеж позволит вам сделать додекаэдр. Для этого нужно начертить такую схему на жесткой бумаге или картоне, затем вырезать по границам и согнуть вдоль внутренних сплошных линий так, чтобы одинаково обозначенные стороны оказались вместе
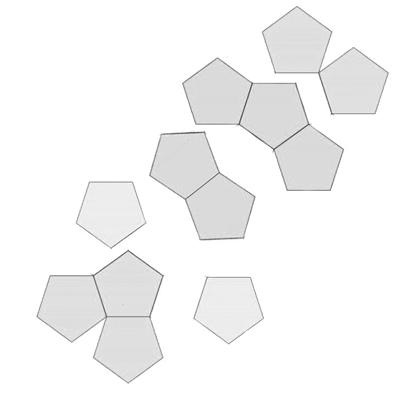
Илл. 39. С разделенной на части схемой изображение становится более трудным для интерпретации, но очевидные намеки на его происхождение остаются. Знакомство с додекаэдром приведет нас от этого набора кусочков обратно к илл. 38 и оттуда к нашему платонову додекаэдру
Здесь труднее понять, что мы видим. Большинство людей, которые в последнее время, возможно, не очень-то думали о додекаэдрах, не знало бы, что сделать с этой неполной схемой. Но те из нас, кто медитировал о красоте и ее воплощениях, подготовлены к этому испытанию. Двенадцать идентичных, правильных пятиугольников, у некоторых пар общая сторона, некоторые тройки готовы образовать вершины – это сразу наводит на мысль! Мы распознаем скрытый потенциал чертежа и готовы сделать из него что-то красивое.
Помня об этом триумфе, давайте теперь возвратимся к нашей Главной теории. Она описывает огромное изобилие фактов – точных количественных наблюдений о физическом мире – с помощью очень небольшого набора уравнений. Она является, как мы уже обсуждали, более чем достаточной основой для химии, инженерного дела, биологии (вероятно), астрофизики и большей части космологии. К тому же она изящна. У уравнений Главной теории есть глубокие корни в симметрии. Поэтому мы можем восстановить всю Главную теорию из нескольких общих правил о том, к каким пространствам свойств имеют доступ различные частицы, и указаний о том, какой (локальной) симметрией должны обладать эти пространства. Мы можем указать необходимые данные на достаточно простых резюмирующих иллюстрациях (см. вклейки TT и UU).
Главная теория замечательно описывает Природу. Было бы трудно преувеличить ее точность, ее мощь или ее красоту. И все же ценители предельной красоты не будут удовлетворены. Именно потому, что она так близка к окончательному описанию Природы, мы должны поддерживать Главную теорию на максимально возможном уровне эстетических стандартов. Если тщательно исследовать ее в таком критическом духе, Главная теория обнаруживает недостатки.
• Она содержит три математически похожих взаимодействия: сильное, слабое и электромагнитное. Все они являются воплощением общего принципа: локальной симметрии пространств свойств. И гравитация – это четвертое взаимодействие. Она также основана на локальной симметрии, хотя и другого рода: локальной галилеевой симметрии. Гравитация также является намного более слабой, чем другие взаимодействия. Было бы убедительнее и красивее иметь одну основную симметрию и одно всеобщее взаимодействие, которые бы давали согласованное описание Природы. Три (или четыре) определенно больше одного, следовательно, мы еще не пришли к цели.
• Что еще хуже, даже после того, как мы установили частицы, которые «на самом деле» являются одной и той же сущностью, по-разному расположенной в своем пространстве, мы оказываемся с шестью не связанными между собой «фундаментальными» объектами. Шесть также определенно больше одного.
• У нас также есть утроение семейств, которое представляется бессмысленным.
• У нас также есть флюид Хиггса, который играет уникальную и важную роль в теории, но пока выглядит еще одной независимой движущейся частью. Флюид Хиггса был введен, чтобы залатать дыры (что он и делает), а не для красоты (и он ее не добавляет).
Нужно признать, что в целом это, конечно, топорная громоздкая конструкция, и суровый критик мог бы назвать ее беспорядочной.
Мог ли Мастер, когда Он грубо высек Главную теорию, сказать, что уже хорошо поработал, и остановиться на этом?
Прежде чем согласиться с этой скандальной мыслью, давайте возвратимся к уроку додекаэдра. Мы видели на его примере, как красота – и, в частности, симметрия – предлагает захватывающую интерпретацию того, что иначе могло бы показаться случайным беспорядком. Понимание возможных симметрий объектов в пространстве привело нас к осознанию того, что есть только горстка платоновых тел, и это знание позволило нам узнать лежащий в основе додекаэдр по частичным, искаженным признакам.
Главная теория основана на более сложных формах симметрии, чем вращения обычного трехмерного пространства, и на менее привычных нам объектах (пространства свойств), чем додекаэдр. Однако мы можем проверить похожую идею. Возможно ли, что фрагментарная симметрия Главной теории и выглядящие кособокими и разрозненными объекты, на которые она распространяется, является частью большей симметрии, действующей на больший объект, связи которого были скрыты от нашего взгляда?
Если мы найдем положительный ответ на этот математический вопрос, то это подскажет нам новые физические теории, которые могли бы преодолеть недостатки Главной теории. Янг и Миллс показали нам, как, сделав предположение о симметрии и о ее действии на пространства свойств, создать соответствующую теорию взаимодействий и частиц. В такой конструкции симметрии воплощаются их аватарами, калибровочными частицами (например, цветными глюонами, виконами, фотонами), с помощью которых переносятся взаимодействия. Наша гипотетическая большая симметрия даст нам всем эти взаимодействия в Главной теории и даже больше.
Благодаря математикам конца XIX и начала XX вв. – Софусу Ли и его последователям – у нас есть полный набор кандидатов на роль той самой симметрии и того самого пространства, так что мы можем посмотреть, отвечает ли какой-то из кандидатов всем требованиям. Так же как существует всего несколько правильных многогранников, оказывается, что существует всего несколько кандидатов на роль большей симметрии, которые могли бы объединить симметрии Главной теории (подобно вращениям додекаэдра), и еще меньше разумных возможностей для пространств свойств, которые могут объединить таковые пространства Главной теории (как грани додекаэдра).
Когда возможности столь ограничены, успех сомнителен. Если перекошенное, разобщенное изображение на илл. 39 было бы перекошено и разъединено по-другому – скажем, три пятиугольника окружали бы треугольную дыру, или их было бы тринадцать, или пятиугольники были бы разных размеров, или там была бы смесь пятиугольников и квадратов – наша попытка объяснить, что это такое, основываясь на скрытой симметрии, потерпела бы неудачу. Точно так же перекошенная, разобщенная структура Главной теории должна быть перекошена и разобщена тем самым правильным способом, чтобы соответствовать схеме большей симметрии. Поэтому, если мы действительно найдем схему, которая будет соответствовать, это вряд ли будет совпадением. Вероятно, находка будет что-то значить!
Поэтому приятно обнаружить, что одна из возможных симметрий Ли, действующих в красивом пространстве свойств, хорошо согласуется с действительностью. Объединяющая симметрия содержит сильно-слабо– электромагнитные симметрии Главной теории. Она может действовать в пространстве свойств, у которого именно тот правильный размер и форма, чтобы вместить известные кварки и лептоны. И самое главное, она не содержит ничего другого. (Для экспертов: симметрия основана на группе вращений в десяти измерениях, обозначаемой SO (10). Пространство свойств основано на 16-мерном спинорном представлении этой группы. Эта структура была обнаружена Говардом Джорджи и Шелдоном Глэшоу.)
Пожалуйста, сделайте сейчас перерыв, чтобы хорошо рассмотреть вклейки VV и WW, которые документируют это открытие. Последующее обсуждение обстоятельно объясняет эти иллюстрации, являясь своего рода развернутой подписью к ним. Вы найдете в нем всю информацию, которую вам нужна, чтобы понять, как вклейки VV и WW кодируют содержание вклеек RR и SS, суммирующих Главную теорию. Основной поток нашей медитации полагается только на подробное описание в тексте. Более тонкие детали украшают последние страницы в примечаниях. Мне показалось важным сделать подробности этого изумительного результата доступными для ознакомления. Вы сами можете решить, насколько глубоко хотели бы в них погрузиться.
Частицы Главной теории в этой новой теории населяют шесть отдельных пространств свойств различной формы, как описано в предыдущей главе. Иначе мы можем сказать, что они образуют шесть различных сущностей.
В нашей объединенной теории большая симметрия соединяет эти пространства свойств, сводя все частицы в единую сущность, или мультиплет. Это объединение материи повторяет то объединение, которого мы достигли для разъединенных, кривых частей нашего таинственного рисунка, когда мы распознали их принадлежность к додекаэдру. Точно так же, как стороны додекаэдра все связаны посредством соответствующих вращений, здесь все частицы связаны друг с другом математической симметрией – и так же посредством конкретных физических преобразований!
На вклейках VV и WW в верхнем левом углу страницы мы видим довольно абстрактную таблицу из знаков + и −. В ней 5 столбцов и 16 строк. Различные строки содержат все возможные распределения пяти знаков + и − с тем ограничением, что общее количество знаков + должно быть четным.
Верхний правый угол начинает процесс разворачивания этой абстрактной схемы в физическую реальность. Структура таблицы остается такой же, но теперь столбцы интерпретируются как представления различных сильных и слабых цветовых зарядов (позднее выяснится, что строки представляют частицы вещества). Первые три столбца соответствуют трем сильным цветовым зарядам: красному, зеленому и синему в указанном порядке. Последние два столбца отображают два слабых цветовых заряда: желтый и фиолетовый. Мы преобразуем нашу предыдущую таблицу со знаками + и − в новый формат, помещая небольшие закрашенные кружочки соответствующего цвета в ячейки, где были знаки +, и небольшие полые кружочки соответствующего цвета туда, где были знаки −.
Закрашенные кружочки (полученные из знаков +) будут интерпретироваться как ½ от единицы заряда. Таким образом, закрашенный красный кружок соответствует половине единицы красного цветового заряда и т. д. (Гениальность этого множителя, ½ , вскоре проявится.) Полые круги (полученные из знаков −) будут интерпретироваться как – ½ заряда.
Под двумя верхними таблицами выписана математическая формула, определяющая величину Y как простую числовую комбинацию цветов. Вспомните, что в перечне компонентов вещества в Главной теории, изображенном на вклейках RR и SS, были странные числа, соответствующие электрическим зарядам. Эти странные заряды в рамках Главной теории были независимы от сильных и слабых цветов – их просто выбрали так, чтобы соответствовать результатам экспериментов. Совсем скоро вы увидите, как эти гадкие утята Главной теории вырастают в великолепных лебедей в нашей объединенной теории. А пока заметьте только, что я записал значения Y , которые мы получаем, применяя формулу к разным строкам, в среднем столбце между двумя верхними таблицами.
Левый нижний угол – всего лишь копия правого верхнего угла, продублированная там для простоты чтения. Точно так же воспроизведен и средний столбец чисел.
Нижняя правая таблица – результат переработки и упрощения левой нижней с применением сильного и слабого правил «отбеливания». Позвольте мне пошагово показать вам этот процесс для первой строки; для остальных мы действуем таким же образом. Согласно сильному правилу «отбеливания», равная смесь красного, зеленого и синего зарядов никак не влияет на сильное взаимодействие. Поэтому мы можем упростить наше описание сильных цветовых зарядов частицы в первой строке, в той ее части, где мы имеем дело с сильным взаимодействием, добавляя половину заряда к каждому красному, зеленому и синему заряду. Эта операция уничтожает существовавшие до того отрицательные половинки зеленого и синего зарядов и увеличивает красный заряд до единицы. В правой нижней таблице мы изображаем результат – большой красный кружок – и уже ничего не проставляем на месте зеленого и синего. Возвращаясь к слабой части строки, мы добавляем по половинке заряда к желтому и фиолетовому и проводим затем слабое «отбеливание», чтобы получить полный желтый заряд и нулевой фиолетовый заряд.
И теперь волшебство раскрыто! Список частиц и свойств, к которому мы приходим, шаг за шагом перерабатывая начальную абстрактную таблицу в верхнем левом углу, точно соответствует перечню компонентов вещества Главной теории (вклейки RR и SS). Первая строка, например, соответствует верхней левой записи сущности A. Стандартные имена частиц показаны на вклейках VV и WW в последнем столбце правой нижней таблицы, и они помогут вам в поиске.
Это упражнение приносит истинную радость, и я настоятельно рекомендую вам проследить за каждым из 16 соответствий. Прежде чем вы попробуете его выполнить, есть одна, последняя тонкость, которая все еще нуждается в упоминании. Правые частицы Главной теории представлены здесь через их левые античастицы. Поэтому, если вы видите знак − перед названием, вы должны обратить знаки всех зарядов (включая Y ) и искать соответствие среди правых частиц.
Это завершает нашу «подробную подпись» к иллюстрации.
Каков же итог? Глядя на строки таблиц на канонических объединительных вклейках VV и WW, мы находим в них идеальное соответствие частицам вещества Главной теории, показанным в ее каноническом синтезе на вклейках RR и SS! Там мы изучили мир – Реальный мир – и классифицировали его частицы. Здесь наш отправной пункт был совсем другим. Мы начали с Идеального – с пространства большей симметрии, выдвинутого в качестве кандидата на пространство свойств, – и вывели математически свойства частиц, которые содержатся в его теории локальной симметрии (Янга – Миллса). Пройдя двумя столь разными путями, мы прибыли в один и тот же пункт назначения. Новый путь – это более объединенное, принципиальное описание. Оно содержит большую часть того, что мы знаем о мире Материи, в построении, созданном чистым Разумом. Это великолепный пример, когда:
Реальное ↔ Идеальное.
Проверка реальностью
Если это верно, тогда это…
Математика симметрии открыла заманчивую перспективу. Она схематично изобразила путь, ведущий от красивых идей к управляющей миром Главной теории и за ее пределы. Все это напоминает своей эстетической вдохновленностью и смелостью атомизм Платона, но все же несравнимо более сложный и точный.
Но возникает две серьезные проблемы, когда мы пытаемся развить этот грубый эскиз до портрета реальности. Одну просто решить, другая – более сложная. Она завлечет нас в интересное приключение, конечная точка которого до сих пор не ясна.
Давайте начнем с более простой. Расширенная теория содержит гораздо больше калибровочных частиц (частиц взаимодействий), чем Главная теория, и поэтому гораздо больше трансформирующих взаимодействий. А именно: у нас имеются не только цветные глюоны, которые превращают один сильный цветовой заряд в другой, и виконы, которые превращают один слабый заряд в другой, но также и мутатроны, которые превращают единицу сильного цветового заряда в единицу слабого цветового заряда. (В литературе нет никакого устоявшегося названия для этих частиц, поэтому я придумал это. Смысл шутки в том, что мутатроны производят мутации.) Например, есть мутатрон, который преобразовывает единицу красного заряда в единицу фиолетового заряда. Эта операция преобразует первую строку вклеек VV и WW в 15-ю, как вы можете сами проверить. Следовательно, взаимодействие с этим конкретным мутатроном превратит красный кварк в позитрон. Но таких процессов никогда не наблюдалось. Если мутатроны существуют, почему мы не видели их эффектов?
К счастью, эта проблема очень похожа на проблему, с которой мы столкнулись в теории слабого взаимодействия и решили ее. Как вы можете вспомнить, «чистая» локальная симметрия предсказывает, что виконы, подобно фотонам и цветным глюонам, обладают нулевой массой. Но если бы это было так, то их влияние было бы намного более мощным, чем то, которое фактически наблюдается. Эту проблему решает механизм Хиггса. Заполняя пространство соответствующим веществом, теоретики сделали виконы тяжелыми и согласовали Реальное с Идеальным. До фактического открытия частицы Хиггса многие физики скептически относились к этой смелой идее[80], но теперь Природа очень красноречиво засвидетельствовала это сама.
Расширенная версия той же самой простой идеи способна придать очень большие массы нежелательным мутатронам объединенной теории и тем самым подавить все их нежелательные эффекты. Мы просто заполняем мир – или, если выразиться скромнее (и точнее), мы признаем, что мир уже заполнен – (выборочно) дающим массу веществом и идем дальше.
Теперь давайте обратимся к более сложной проблеме. Если мы рассчитываем установить симметрию среди различных взаимодействий, то у этих взаимодействий должна быть одинаковая интенсивность. Это прямое следствие их предполагаемой эквивалентности. Но вот незадача – это не так. Сильное взаимодействие действительно сильнее, чем другие взаимодействия. Три основных взаимодействия совершенно определенно не равны по силе (а гравитация, на первый взгляд, безнадежно слаба по сравнению с ними).
(Важное, но немного техническое отступление: я должен приостановиться, чтобы объяснить, как делается сравнение. Основная идея – сама простота. Каждое из наших взаимодействий, основанных, как повелось, на уравнениях, похожих на уравнения Максвелла, действует между заряженными частицами. Для электромагнитных взаимодействий имеет значение электрический заряд, для сильных взаимодействий – цветовой заряд, а для слабых взаимодействий – слабый цветовой заряд. Для каждого из наших взаимодействий есть единица [квант] заряда. Поэтому, чтобы сравнить взаимодействия, обычно просто сравнивают силу взаимодействия между единичными зарядами.
На практике все немного сложнее по двум причинам. Во-первых, эффект слабого взаимодействия подавляется на расстояниях более 10−16 см, а действие сильного взаимодействия незаметно на расстояниях более 10−14 см по интересным, но непростым причинам, которые мы затронули ранее (механизм Хиггса и конфайнмент соответственно). Поэтому, чтобы сделать справедливое сравнение, следует сравнивать их только на расстояниях меньших, чем эти. Во-вторых, не слишком практично иметь дело с частицами в пространстве с таким высоким уровнем точности.
Что экспериментаторы делают в действительности, чтобы исследовать поведение на маленьких расстояниях, так это стреляют частицами друг по другу и изучают вероятность отклонения на (относительно) большие углы. Затем мы восстанавливаем картину, реконструируя по отклонениям частиц те силы, которые их вызывали. Вы можете вспомнить, что именно такой была стратегия, которую Резерфорд, Гейгер и Марсден использовали для изучения внутреннего строения атомов около 1912 г. Основной принцип не изменился, но сегодня, сталкивая частицы с гораздо большей энергией, мы получаем доступ к более коротким расстояниям.
Сравнение других взаимодействий с гравитацией несколько хитрее. С одной стороны, насколько нам известно, нет никакой фундаментальной «единицы заряда» для гравитации – она реагирует на энергию. С другой стороны, мы используем пробные объекты, которые имеют различную энергию, чтобы сравнивать взаимодействия на различных расстояниях. Поэтому при оценке относительной силы гравитации на этих расстояниях мы просто подставляем в уравнения энергию, соответствующую этому расстоянию, и вычисляем гравитационную силу, с которой она действует. Конец технического отступления.)
