Неинерциальные системы отсчета и силы инерции
Как уже отмечалось нами, законы Ньютона выполняются только в инерциальных системах отсчета. Системы отсчета, движущиеся относительно инерциальной системы с ускорением, называютсянеинерциальными. В неинерциальных системах законы Ньютона, вообще говоря, уже несправедливы. Однако законы динамики можно применять и для них, если кроме сил, обусловленных воздействием тел друг на друга, ввести в рассмотрение силы особого рода — так называемыесилы инерции.
Если учесть силы инерции, то второй закон Ньютона будет справедлив для любой системы отсчета:
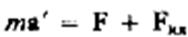(27.1)
Так как F=ma (a — ускорение тела в инерциальной системе отсчета), то
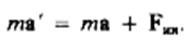
Силы инерции при ускоренном поступательном движении системы отсчета.
Пусть на тележке к штативу на нити подвешен шарик массой т . Пока тележка покоится или движется равномерно и прямолинейно, нить, удерживающая шарик, занимает вертикальное положение и сила тяжести Р уравновешивается силой реакции нити Т.
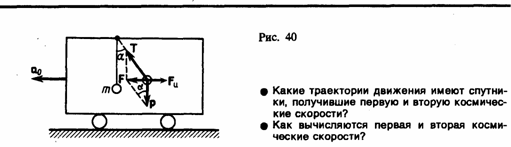
Если тележку привести в поступательное движение с ускорением а0, то нить начнет отклоняться от вертикали назад до такого угла , пока результирующая сила F=P+T не обеспечит ускорение шарика, равное а0. Таким образом, результирующая сила F направлена в сторону ускорения тележки а0 и для установившегося движения шарика равна F=mgtgα=ma, откуда
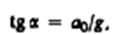
т. е. угол отклонения нити от вертикали тем больше, чем больше ускорение тележки.
Относительно системы отсчета, связанной с ускоренно движущейся тележкой, шарик покоится, что возможно, если сила F уравновешивается равной и противоположно направленной ей силой Fи, которая является ничем иным, как силой инерции, так как на шарик никакие другие силы не действуют. Таким образом,
(27.2)
Центробежная сила – сила инерции первого рода. Центробежной силы, приложенной к вращающемуся телу, не существует.
С точки зрения наблюдателя, связанного с неинерциальной системой отсчета, он не приближается к центру, хотя видит, что Fцс действует .Следовательно, с точки зрения наблюдателя в неинерциальной системе есть сила, уравновешивающая Fцс, равная ей по величине и противоположная по направлению:
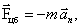
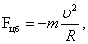
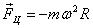— центробежная сила инерции, действующая на тело относительно вращающейся НСО
Пример действия центробежной силы - выжимание белья в центрифуге (вода при вращении оттесняется в стенке барабана)
При движении тела относительно вращающейся системы отсчета, кроме центростремительной и центробежной сил, появляется еще одна сила, называемая силой Кориолиса.
Появление кориолисовой силы можно обнаружить на следующем примере. Возьмем горизонтально расположенный диск, который может вращаться вокруг вертикальной оси. Прочертим на диске радиальную прямую ОА.
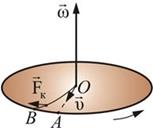
Запустим в направлении от О к А шарик со скоростью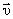 
. Если диск не вращается, шарик должен катиться вдоль ОА. Если же диск привести во вращение в направлении, указанном стрелкой, то шарик будет катиться по кривой ОВ, причем его скорость относительно диска быстро изменяет свое направление. Следовательно, по отношению к вращающейся системе отсчета шарик ведет себя так, как если бы на него действовала сила 
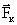, перпендикулярная направлению движения шарика.
Чтобы заставить шарик катиться вдоль ОА, нужно сделать направляющую, выполненную в виде ребра. При качении шарика направляющее ребро действует на него с некоторой силой. Относительно вращающейся системы (диска), шарик движется с постоянной по направлению скоростью. Это можно объяснить тем, что эта сила уравновешивается приложенной к шарику силой инерции:
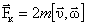 | (4.5.5) |
Здесь 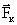– сила Кориолиса, также являющаяся силой инерции, 
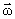– угловая скорость вращения диска.
16)
Уравнение гармонических колебаний
Уравнение (1)
|
Однако обычно под уравнением колебаний понимают иную запись этого уравнения, в дифференциальной форме. Возьмем для определенности уравнение (1) в виде
дважды продифференцируем его по времени:
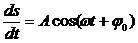
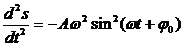
Видно, что выполняется следующее соотношение:
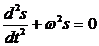(2)
которое и называется уравнением свободных гармонических колебаний (в дифференциальной форме). Уравнение (1) является решением дифференциального уравнения (2). Поскольку уравнение (2) - дифференциальное уравнение второго порядка, необходимы два начальных условия для получения полного решения
