Формулировка закона сохранения механической энергии.

Полная механическая энергия, т.е. сумма потенциальной и кинетической энергии тела, остается постоянной, если действуют только силы упругости и тяготения и отсутствуют силы трения.

В замкнутой системе, в которой действуют только консервативные силы, механическая энергия сохраняется.Если между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание).Диссипативные системы , механические системы, полная энергия которых при движении убывает, переходя в другие виды энергии, напр. в теплоту, т. е. происходит диссипация энергии.

9)

Абсолютно неупругий удар – это столкновение двух тел, в результате которого тела объединяются и двигаются дальше, как единое целое.

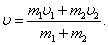
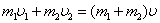Продемонстрировать абсолютно неупругий удар можно также с помощью шаров из пластилина (глины), движущихся навстречу друг другу. Если массы шаров m₁ и m₂, их скорости до удара 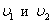, то, используя закон сохранения импульса, можно записать:

где 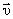– скорость движения шаров после удара.

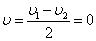Если шары двигались навстречу друг другу, то они вместе будут продолжать двигаться в ту сторону, в которую двигался шар, обладающий большим импульсом. В частном случае – если массы и скорости шаров равны, то

Абсолютно упругий удар - соударение двух тел, в результате которого в обоих участвующих в столкновении телах не остается никаких деформаций и вся кинетическая энергия тел до удара после удара снова превращается в первоначальную кинетическую энергию

Обозначим скорости шаров массами m₁ и m₂ до удара через ν₁ и ν₂, после удара - через ν₁' и ν₂'

При указанных допущениях законы сохранения имеют вид

(1)

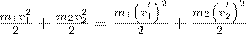(2)

Произведя соответствующие преобразования в выражениях (1) и (2), получим

(3)

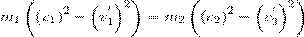(4)
откуда

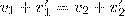(5)

Решая уравнения (3) и (5), находим

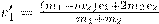(6)

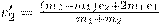(7)

10)

Момент импульса частицы:

Моментом импульса (количества движения)материальной точки Аотносительно неподвижной точки Оназывается физическая величина, определяемая векторным произ­ведением:

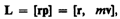
где r — радиус-вектор, проведенный из точки О в точку A, p=mv — импульс материальной точки

Моментом импульса относительно неподвижной оси z называется скалярная величина L_z, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Момент импульса L_z не зависит от положения точки О на оси z.

При вращении абсолютно твердого тела вокруг неподвижной оси z каждая отдель­ная точка тела движется по окружности постоянного радиуса r_i с некоторой скоро­стью v_i . Скорость v_i и импульс m_iv_i перпендикулярны этому радиусу, т. с. радиус является плечом вектора m_iv_i . Поэтому можем записать, что момент импульса отдель­ной частицы равен

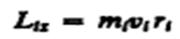
Момент силы относительно точки О - это вектор, модуль которого равен произведению модуля силы на плечо - кратчайшее расстояние от точки О до линии действия силы. Направление вектора момента силы перпендикулярно плоскости, проходящей через точку и линию действия силы, так, что глядя по направлению вектора момента, вращение, совершаемое силой вокруг точки О, происходит по часовой стрелке.

Если известен радиус-вектор r⃗ точки приложения силы F⃗ относительно точки О, то момент этой силы относительно О выражается следующим образом:

M⃗ O(F⃗ )=r⃗ ×F⃗ .

Действительно, модуль этого векторного произведения:

|M⃗ O|=|r⃗ ×F⃗ |=|r⃗ ||F⃗ |sinα.

В соответствии с рисунком |r⃗ |sinα=h, поэтому:

|M⃗ O|=|F⃗ |h.

Момент силы считается положительным, если сила стремится повернуть тело вокруг центра О против хода часовой стрелки и отрицательным, если по ходу часовой стрелки

Момент силы не изменяется при переносе точки приложения силы вдоль ее линии действия. Момент силы относительно центра О равен нулю, если сила равна нулю или, если линия действия силы проходит через центр О (плечо рав-но нулю). Графически абсолютная величина момента силы относительно центра О вы-ражается удвоенной площадью ОАВ

Закон сохранения момента импульса: момент импульса замкнутой системы тел относительно любой неподвижной точки не изменяется с течением времени.

Для замкнутой системы тел момент внешних сил всегда равен нулю, так как внешние силы вообще не действуют на замкнутую систему.
Поэтому ,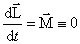

Момент импульса и для незамкнутых систем постоянен, если результирующий момент внешних сил, приложенных к системе, равен нулю.